Distance d'un point à une droite

Distance d'un point à une droite
La distance entre le point A et la droite (d ) est la distance AAh

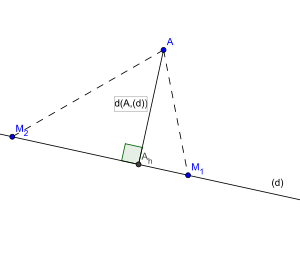
En géométrie euclidienne, la distance d'un point à une droite est la plus courte distance séparant ce point et un point courant de la droite. Le théorème de Pythagore permet d'affirmer que la distance du point A à la droite (d ) correspond à la distance séparant A de son projeté orthogonal Ah sur la droite (d ). On peut ainsi écrire :

d(A,(d)) = d(A,Ah)

Dans le plan

Si le plan est muni d'un repère orthonormal, si la droite (d) a pour équation ax + by + c = 0 et si le point A a pour coordonnées (xA ; yA), alors la distance entre A et (d ) est donnée par la formule

d(\mathrm{A}, (d)) = \mathrm{AA}_h = \frac{|ax_A+by_A+c|}{\sqrt{a^2+b^2}}

où |r | représente la valeur absolue du réel r.

En effet, si M(x, y ) est un point quelconque de la droite (d ), et si on note \vec n le vecteur normal à la droite (d ) de composantes (a ; b ), alors la valeur absolue du produit scalaire des vecteurs \overrightarrow{\mathrm{AM}} et \vec n est donnée par les deux expressions :

|\overrightarrow{\mathrm{AM}} \cdot \vec n | = |a(x-x_\mathrm{A}) + b(y - y_\mathrm{A})|= |ax_\mathrm{A} + by_\mathrm{A} + c| ( ax + by = - c car M est un point de (d))
|\overrightarrow{\mathrm{AM}} \cdot \vec n| = \mathrm{AA}_h \times ||\vec n|| = \mathrm{AA}_h\times \sqrt{a^2+b^2}.

En particulier,

  • si la droite a pour équation y = mx + p alors d(\mathrm{A}, (d))=\frac{|mx_\mathrm{A} - y_\mathrm{A} + p |}{\sqrt{1+m^2}}
  • si la droite a pour équation x = a alors d(A,(d)) = | xA − a |  ;
  • si la droite a pour équation y = b alors d(A,(d)) = | yA − b | .

Dans l'espace

Si l'espace est muni d'un repère orthonormal, si la droite (d ) passe par le point B et a pour vecteur directeur \vec u, la distance entre le point A et la droite (d) est donnée par la formule

d(\mathrm{A}, (d))= \frac{\left\|\overrightarrow{\mathrm{BA}} \wedge \vec u\right\|}{\|\vec u\|}

où \vec BA \wedge \vec u représente le produit vectoriel des vecteurs \vec BA et \vec u et où \|\vec u\| représente la norme du vecteur \vec u.

En effet, si l'on note C le point de (d ) tel que \overrightarrow{\mathrm{BC}}=\vec u alors l'aire du triangle ABC est donnée par les deux expressions

\mathrm{A}_{\mathrm{ABC}} = \frac{1}{2} \left\|\overrightarrow{\mathrm{BA}} \wedge \overrightarrow{\mathrm{BC}} \right\|
\mathrm{A}_{\mathrm{ABC}} = \frac{1}{2} \mathrm{BC} \times \mathrm{AA}_h.

Cette distance est supérieure ou égale à toute distance séparant le point A d'un plan contenant la droite (d ). Si la droite (d ) est définie comme l'intersection de deux plans perpendiculaires et si l'on note d₁ et d₂ les distances du point A à ces deux plans, on a :

d(\mathrm{A}, (d))= \sqrt{{d_1}^2+{d_2}^2}.

Voir aussi


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Distance d'un point à une droite de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Distance D'un Point À Un Plan Dans L'espace Cartésien — Distance d un point à un plan Dans l espace euclidien, la distance d un point à un plan est la plus courte distance séparant ce point et un point du plan. Le théorème de Pythagore permet d affirmer que la distance du point A au plan (P)… …   Wikipédia en Français

  • Distance d'un point a un plan dans l'espace cartesien — Distance d un point à un plan Dans l espace euclidien, la distance d un point à un plan est la plus courte distance séparant ce point et un point du plan. Le théorème de Pythagore permet d affirmer que la distance du point A au plan (P)… …   Wikipédia en Français

  • Distance d'un point à un plan dans l'espace cartésien — Distance d un point à un plan Dans l espace euclidien, la distance d un point à un plan est la plus courte distance séparant ce point et un point du plan. Le théorème de Pythagore permet d affirmer que la distance du point A au plan (P)… …   Wikipédia en Français

  • Distance d'un point à un plan — La distance du point A au plan P est AH. Cette distance est inférieure à AM et AM Dans l espace euclidien, la distance d un point à un plan est la plus courte distance séparant ce point et un point du plan. Le théorème de Pythagore permet d… …   Wikipédia en Français

  • distance — [ distɑ̃s ] n. f. • 1223; lat. distantia 1 ♦ Longueur qui sépare une chose d une autre. ⇒ 1. écart, écartement, éloignement, 1. espace, étendue, intervalle. Distance entre deux lieux. Distance d un point à un autre, de la Terre à la Lune. Évaluer …   Encyclopédie Universelle

  • Distance (Mathématiques) — Pour les articles homonymes, voir Distance. En mathématiques, une distance est une application qui formalise l idée intuitive de distance, c est à dire la longueur qui sépare deux points. Sommaire 1 Distance sur un ensemble …   Wikipédia en Français

  • Distance (mathematiques) — Distance (mathématiques) Pour les articles homonymes, voir Distance. En mathématiques, une distance est une application qui formalise l idée intuitive de distance, c est à dire la longueur qui sépare deux points. Sommaire 1 Distance sur un… …   Wikipédia en Français

  • Distance euclidienne — Distance (mathématiques) Pour les articles homonymes, voir Distance. En mathématiques, une distance est une application qui formalise l idée intuitive de distance, c est à dire la longueur qui sépare deux points. Sommaire 1 Distance sur un… …   Wikipédia en Français

  • Distance (mathématiques) — Pour les articles homonymes, voir Distance. En mathématiques, une distance est une application qui formalise l idée intuitive de distance, c est à dire la longueur qui sépare deux points. C est par l analyse des principales propriétés de la… …   Wikipédia en Français

  • point — 1. point [ pwɛ̃ ] n. m. • 1175 « endroit, moment »; lat. punctum « piqûre », de pungere → poindre I ♦ A ♦ Portion de l espace déterminée avec précision. 1 ♦ Endroit, lieu. En divers, en plusieurs points. « il relevait la tête et fixait son regard …   Encyclopédie Universelle

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”