Chute d'une plaque collee par un fluide visqueux

Chute d'une plaque collee par un fluide visqueux

Chute d'une plaque collée par un fluide visqueux

Soit une plaque circulaire collée au plafond par une goutte de shampoing. Tombera-t-elle, et si oui, en combien de temps ?

Le poids de la plaque a tendance à la faire tomber. La capillarité tend à maintenir la plaque en place. Une fois la plaque en mouvement, la viscosité du liquide la ralentit. Enfin, lorsque la plaque est presque entièrement détachée, son inertie entre en jeu (et son accélération doit donc être prise en compte).

Sommaire

Notations

Pour calculer ces forces et leurs effets, nous notons R le rayon de la goutte écrasée, h son épaisseur, et 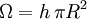\Omega=h\,\pi R^2 son volume, qui est constant. M désigne la masse de la plaque, et g l'accélération de la pesanteur.

Force capillaire

L'adhésion capillaire retient la plaque au plafond. Son origine est la suivante.

La goutte de shampoing, écrasée entre la plaque et le plafond, est devenue un mince film. Le bord de ce film est constitué d'une surface courbe, appelée ménisque, qui se raccorde à la plaque et au plafond. Ce ménisque est en général fortement incurvé lorsque le film est mince. Par conséquent, la pression dans le film est abaissée (pression de Laplace). Cette dépression, multipliée par la surface qu'occupe la goutte, constitue la force capillaire.


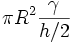
\pi R^2 \frac{\gamma}{h/2}

Ici, nous avons supposé, pour simplifier, que le shampoing mouille totalement la plaque ainsi que le plafond. Le rayon de courbure du ménisque est alors h / 2.

Critère de mise en mouvement de la plaque

Si la plaque est légère, la force capillaire est suffisante pour la maintenir collée au plafond :

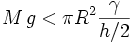
M\,g < \pi R^2 \frac{\gamma}{h/2}

Si elle est plus lourde, elle se met en mouvement. Une force visqueuse ralentit alors sa chute.

De manière équivalente, pour une plaque donnée (de masse fixée), on peut définir une épaisseur critique de mise en mouvement :

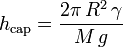
h_{\rm cap}=\frac{2\pi\,R^2\,\gamma}{M\,g}

Si h < hcap, la force capillaire est supérieure au poids, et la plaque mobile se rapproche de la plaque supérieure. À l'inverse, si h > hcap, le poids l'emporte sur la force capillaire, et la plaque amorce sa chute.


Force visqueuse

Lorsque la plaque se met en mouvement, elle induit un écoulement du shampoing, et il en résulte une force qui tente de s'opposer à sa chute.

Cette force ne fait que ralentir la chute et ne peut la stopper. En effet, elle s'éteint si le mouvement cesse.

Cette force s'exprime de la manière suivante (voir le calcul de cette force) :

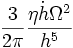
\frac{3}{2\pi}\frac{\eta \dot{h} \Omega^2}{h^5}

note : l'analyse dimensionnelle vérifie que : 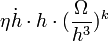\eta \dot{h}\cdot h \cdot ({\Omega \over h^3})^k  ; ici k = 2.

Équation complète et temps de chute

Le produit de la masse et de l'accélération est égal à la somme des forces : le poids, la force capillaire, et la force visqueuse. Ainsi :

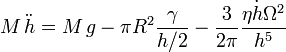
M\,\ddot{h} = M\,g - \pi R^2 \frac{\gamma}{h/2} - \frac{3}{2\pi}\frac{\eta \dot{h} \Omega^2}{h^5}

Cette équation d'évolution s'intègre pour fournir l'épaisseur de la goutte au cours du temps, h(t). Le temps de chute est la date à laquelle l'épaisseur h(t) diverge.

Évolution simplifiée

Avant que la plaque ne chute de façon visible, elle va tellement lentement que son accélération peut être négligée. Seuls comptent donc son poids, la force capillaire et la force visqueuse. L'équation d'évolution complète devient :

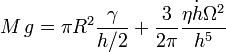
M\,g = \pi R^2 \frac{\gamma}{h/2} + \frac{3}{2\pi}\frac{\eta \dot{h} \Omega^2}{h^5}

Pour simplifier encore, supposons que la plaque soit très lourde. La force capillaire peut alors être négligée. L'équation d'évolution de l'épaisseur de la goutte prend alors uniquement en compte le poids et la force visqueuse :

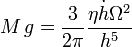
M\,g = \frac{3}{2\pi}\frac{\eta \dot{h} \Omega^2}{h^5}

ou encore :

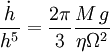
\frac{\dot{h}}{h^5} = \frac{2\pi}{3} \frac{M\,g}{\eta \Omega^2}

Temps de chute dans le cas purement visqueux

Dans le cas où l'on conserve uniquement le poids et la force visqueuse, l'équation d'évolution se résout sous la forme :

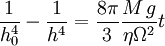
\frac{1}{h_0^4}-\frac{1}{h^4} = \frac{8\pi}{3} \frac{M\,g}{\eta \Omega^2} t

où t est le temps, et h0 l'épaisseur initiale.

Cette équation prédit donc que l'épaisseur h(t) diverge (chute de la plaque) à la date :

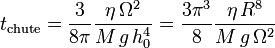
t_{\rm chute} = \frac{3}{8\pi}\frac{\eta\,\Omega^2}{M\,g\,h_0^4} = \frac{3\pi^3}{8}\frac{\eta\,R^8}{M\,g\,\Omega^2}

note : mis à part le 3Pi^3/8 ce résultat était prédictible sans calcul par analyse dimensionnelle, car l'équation différentielle précédente donnait immédiatement : 1/(T h^4) = second membre.

Temps de chute dans le cas visco-capillaire

Dans le cas où seule l'accélération est négligée, l'équation d'évolution s'écrit :

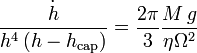
\frac{\dot{h}} {h^4\,(h-h_{\rm cap})} = \frac{2\pi}{3} \frac{M\,g}{\eta \Omega^2}

où hcap est l'épaisseur de mise en mouvement définie plus haut.

L'équation s'écrit :

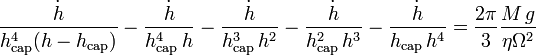
\frac{\dot{h}}{h_{\rm cap}^4(h-h_{\rm cap})} -\frac{\dot{h}}{h_{\rm cap}^4\,h} -\frac{\dot{h}}{h_{\rm cap}^3\,h^2} -\frac{\dot{h}}{h_{\rm cap}^2\,h^3} -\frac{\dot{h}}{h_{\rm cap}\,h^4} = \frac{2\pi}{3} \frac{M\,g}{\eta \Omega^2}

Elle s'intègre :

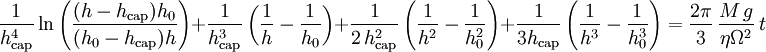
\frac{1}{h_{\rm cap}^4}\ln\left(\frac{(h-h_{\rm cap})h_0}{(h_0-h_{\rm cap})h}\right) +\frac{1}{h_{\rm cap}^3}\left(\frac{1}{h}-\frac{1}{h_0}\right) +\frac{1}{2\,h_{\rm cap}^2}\left(\frac{1}{h^2}-\frac{1}{h_0^2}\right) +\frac{1}{3h_{\rm cap}}\left(\frac{1}{h^3}-\frac{1}{h_0^3}\right) = \frac{2\pi}{3}\,\frac{M\,g}{\eta \Omega^2}\,t

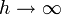Le temps de chute est obtenu dans la limite h\rightarrow\infty :

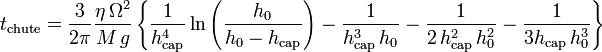
t_{\rm chute} = \frac{3}{2\pi}\frac{\eta\,\Omega^2}{M\,g} \left\{ \frac{1}{h_{\rm cap}^4}\ln\left(\frac{h_0}{h_0-h_{\rm cap}}\right) -\frac{1}{h_{\rm cap}^3\,h_0} -\frac{1}{2\,h_{\rm cap}^2\,h_0^2} -\frac{1}{3h_{\rm cap}\,h_0^3} \right\}

Comme on s'y attend, le temps de chute diverge lorsque l'épaisseur initiale h0 s'approche de l'épaisseur d'équilibre hcap pour laquelle la force capillaire compense exactement le poids.

Dans la limite où la capillarité peut être négligée, cela revient à prendre la limite 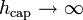h_{\rm cap}\rightarrow\infty, et en développant le logarithme, on retrouve l'expression précédente du temps de chute :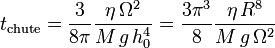

t_{\rm chute} = \frac{3}{8\pi}\frac{\eta\,\Omega^2}{M\,g\,h_0^4} = \frac{3\pi^3}{8}\frac{\eta\,R^8}{M\,g\,\Omega^2}


  • Portail de la physique Portail de la physique
Ce document provient de « Chute d%27une plaque coll%C3%A9e par un fluide visqueux ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Chute d'une plaque collee par un fluide visqueux de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Chute D'une Plaque Collée Par Un Fluide Visqueux — Soit une plaque circulaire collée au plafond par une goutte de shampoing. Tombera t elle, et si oui, en combien de temps ? Le poids de la plaque a tendance à la faire tomber. La capillarité tend à maintenir la plaque en place. Une fois la… …   Wikipédia en Français

  • Chute d'une plaque collée par un fluide visqueux — Soit une plaque circulaire collée au plafond par une goutte de shampoing. Tombera t elle, et si oui, en combien de temps ? Le poids de la plaque a tendance à la faire tomber. La capillarité tend à maintenir la plaque en place. Une fois la… …   Wikipédia en Français

  • VERRE — Les verres constituent un ensemble extrêmement varié de produits dont les propriétés sont innombrables. Celles ci dépendent fortement des traitements subis, thermiques notamment. Leur mise au point résulte aujourd’hui des progrès des… …   Encyclopédie Universelle

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”