Tricercle de Mohr
- Tricercle de Mohr
-
Arbelos
L'arbelos (ou tricercle de Mohr, du nom du mathématicien danois Georg Mohr) est une figure géométrique plane étudiée, entre autres, par Archimède (-287 - -212, Syracuse). Le terme « arbelos » signifie couteau du savetier.
Construction
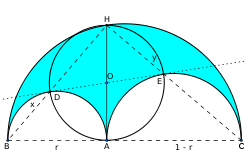
Soit un demi-cercle de diamètre BC. Soit A un point quelconque de ce diamètre.
- Tracer le demi-cercle de diamètre BA intérieur.
- Tracer le demi-cercle de diamètre AC intérieur.
- Considérer la surface intérieure obtenue : c'est une lame d'arbelos.
Propriétés
Cette figure possède de nombreuses propriétés dont voici quelques-unes:
Propriété de l'aire : soit AH la demi-corde verticale passant par A. L'aire de l'arbelos est égale à l'aire du cercle de diamètre AH.
- Démonstration : il suffit d'appeler b et c les diamètres AB et AC, et h la hauteur AH. Les aires des demi-cercles sont alors respectivement de
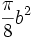 ,
, 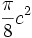 ,
, 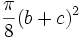 . Puis, par différence, on obtient l'aire de l'arbelos
. Puis, par différence, on obtient l'aire de l'arbelos 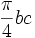 . La dernière étape fait appel aux propriétés du triangle rectangle dans lequel le carré de la hauteur est égal au produit des longueurs découpées sur l'hypoténuse. En d'autres termes : bc = h2. Ce qui nous donne pour l'aire de l'arbelos :
. La dernière étape fait appel aux propriétés du triangle rectangle dans lequel le carré de la hauteur est égal au produit des longueurs découpées sur l'hypoténuse. En d'autres termes : bc = h2. Ce qui nous donne pour l'aire de l'arbelos : 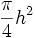 qui est bien l'aire du cercle de diamètre AH
qui est bien l'aire du cercle de diamètre AH
Propriété du rectangle: Le segment BH coupe le demi-cercle BA en D. Le segment CH coupe le demi-cercle AC en E. Alors DHEA est un rectangle
- Démonstration : Les triangles BDA, BHC et AEC sont rectangles car inscrits dans des demi-cercles (théorème de Thalès (cercle). Le quadrilatère ADHE possède donc trois angles droits, c'est un rectangle.
Propriété des tangentes : La droite (DE) est une tangente commune aux deux cercles.
- Démonstration : La similitude de centre D qui envoie B sur A a pour angle π / 2 et envoie aussi A sur H (les triangles DBA et DAH sont semblables). Elle envoie donc le milieu I de [AB] sur le milieu O de [AH] et l'angle IDO est droit. La droite (DO) est donc tangente au premier cercle en D. Comme ADHE est un rectangle, le point O est sur (DE) donc (DE) est une tangente du premier cercle. Elle est tangente du second par un raisonnement analogue.
Voir aussi
Liens internes
Liens externes
 Portail de la géométrie
Portail de la géométrie
Catégories : Forme géométrique | Cercle et sphère
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Tricercle de Mohr de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Cercle De Mohr — Ne doit pas être confondu avec Tricercle de Mohr. Le cercle de Mohr est une représentation graphique des états de contrainte à deux dimensions, proposée par Christian Otto Mohr en 1882. Dans un graphique où l axe horizontal représente l… … Wikipédia en Français
Cercle De Mohr (Temporaire) — Cercle de Mohr Ne doit pas être confondu avec Tricercle de Mohr. Le cercle de Mohr est une représentation graphique des états de contrainte à deux dimensions, proposée par Christian Otto Mohr en 1882. Dans un graphique où l axe horizontal… … Wikipédia en Français
Cercle de Mohr (temporaire) — Cercle de Mohr Ne doit pas être confondu avec Tricercle de Mohr. Le cercle de Mohr est une représentation graphique des états de contrainte à deux dimensions, proposée par Christian Otto Mohr en 1882. Dans un graphique où l axe horizontal… … Wikipédia en Français
Cercle de mohr — Ne doit pas être confondu avec Tricercle de Mohr. Le cercle de Mohr est une représentation graphique des états de contrainte à deux dimensions, proposée par Christian Otto Mohr en 1882. Dans un graphique où l axe horizontal représente l… … Wikipédia en Français
Cercle de mohr (temporaire) — Cercle de Mohr Ne doit pas être confondu avec Tricercle de Mohr. Le cercle de Mohr est une représentation graphique des états de contrainte à deux dimensions, proposée par Christian Otto Mohr en 1882. Dans un graphique où l axe horizontal… … Wikipédia en Français
Cercle de Mohr — Ne doit pas être confondu avec Tricercle de Mohr. Le cercle de Mohr est une représentation graphique des états de contrainte à deux dimensions, proposée par Christian Otto Mohr en 1882. Dans un graphique où l axe horizontal représente l… … Wikipédia en Français
Georgius Mohr — Georg Mohr Jørgen Mohr (plus connu sous le nom de Georg(ius) Mohr) (1er avril, 1640 26 janvier, 1697) est un mathématicien danois qui a exercé aux Pays Bas, en France et Grande Bretagne. Il établit un siècle avant Lorenzo Mascheroni l… … Wikipédia en Français
Jorgen Mohr — Georg Mohr Jørgen Mohr (plus connu sous le nom de Georg(ius) Mohr) (1er avril, 1640 26 janvier, 1697) est un mathématicien danois qui a exercé aux Pays Bas, en France et Grande Bretagne. Il établit un siècle avant Lorenzo Mascheroni l… … Wikipédia en Français
Jørgen Mohr — Georg Mohr Jørgen Mohr (plus connu sous le nom de Georg(ius) Mohr) (1er avril, 1640 26 janvier, 1697) est un mathématicien danois qui a exercé aux Pays Bas, en France et Grande Bretagne. Il établit un siècle avant Lorenzo Mascheroni l… … Wikipédia en Français
Georg Mohr — Jørgen Mohr (plus connu sous le nom de Georg(ius) Mohr) (1er avril, 1640 26 janvier, 1697) est un mathématicien danois qui a exercé aux Pays Bas, en France et Grande Bretagne. Il établit un siècle avant Lorenzo Mascheroni l important… … Wikipédia en Français
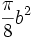 ,
, 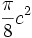 ,
, 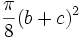 . Puis, par différence, on obtient l'aire de l'arbelos
. Puis, par différence, on obtient l'aire de l'arbelos 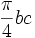 . La dernière étape fait appel aux propriétés du triangle rectangle dans lequel le carré de la hauteur est égal au produit des longueurs découpées sur l'hypoténuse. En d'autres termes : bc = h2. Ce qui nous donne pour l'aire de l'arbelos :
. La dernière étape fait appel aux propriétés du triangle rectangle dans lequel le carré de la hauteur est égal au produit des longueurs découpées sur l'hypoténuse. En d'autres termes : bc = h2. Ce qui nous donne pour l'aire de l'arbelos : 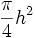 qui est bien l'aire du cercle de diamètre AH
qui est bien l'aire du cercle de diamètre AH