- Cercles d'Apollonius
-
Il y a plusieurs candidats répondant au nom de cercle d'Apollonius'.
Une autre définition du cercle
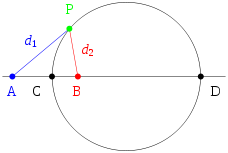
Apollonius de Perga propose de définir le cercle comme l'ensemble des points M du plan pour lesquels le rapport des distances MA/MB reste constant, les points A et B étant donnés. Précisément
Théorème — Si A et B sont deux points distincts et k est un réel autre que 0 et 1, le cercle d'Apollonius du triplet (A,B,k) est l'ensemble des points M du plan tels que MA/MB = k
Démonstration —
- Solution de MA/MB = k sur (AB) : si k=1, MA=kMB a une unique solution sur (AB), le milieu de [AB]. Sinon le problème d'Apollonius MA = k MB a deux solutions sur (AB), disons C et son conjugué harmonique D par rapport à A et B ; D existe dès que C n'est pas le milieu de [AB].
- Solution hors de (AB) :Si MA/MB = k, alors MA/MB = CA/CB ; (MC) est alors la bissectrice de l'angle en M dans le triangle AMB. Mais on a aussi MA/MB = DA/DB et (MD) est la seconde bissectrice de l'angle en M dans AMB. En particulier le triangle CMD est rectangle en M et M est sur le cercle de diamètre [CD].
- Synthèse :Pour tout M du plan hors de (AB) les droites (MA), (MB), (MC) et (MD) forme un faisceau harmonique. Si de plus M est sur le cercle de diamètre [CD], on sait alors que (MC) et (MD) sont les bissectrices de ∠AMB. On conclut avec la caractérisation de la bissectrice en termes de rapport
- Le cercle de diamètre [CD] est le cercle d'Apollonius pour le triplet (A,B,k).
Faisceau de cercles d'Apollonius

Soit ABC un triangle. Le cercle c4 de centre I est circonscrit au triangle ABC.
Les bissectrices en A coupent [BC] en I1 et J1, le cercle c1 de centre O1 a pour diamètre [I1J1].
Les bissectrices en B coupent [AC] en I2 et J2, le cercle c2 de centre O2 a pour diamètre [I2J2].
Les bissectrices en C coupent [AB] en I3 et J3, le cercle c3 de centre O3 a pour diamètre [I3J3].
Le faisceau de cercles d'Apollonius est formé par les trois cercles c1, c2 et c3 d'Apollonius qui ont en commun les deux points P et Q. Ce sont les points de base du faisceau.
Leurs centres O1, O2 et O3 sont alignés sur la médiatrice de [PQ].
Le centre I du cercle circonscrit c4 est situé sur la droite (PQ).
Fractal
Voir : Cercle d'Apollonius
Catégories :- Géométrie du triangle
- Cercle et sphère
Wikimedia Foundation. 2010.