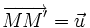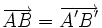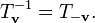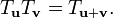Translation (mathematiques elementaires)

Une translation déplace tous les points d'un objet géométrique d'une même distance selon une direction dans le même sens.

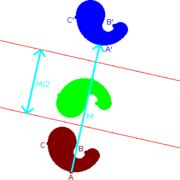Une réflexion selon un axe de symétrie suivie d'une autre réflexion selon un deuxième axe de symétrie parallèle au premier est équivalent à une translation.

En mathématiques, une translation est une transformation géométrique qui correspond à l'idée intuitive de « glissement » d'un objet, sans rotation, retournement ni déformation de cet objet.

Une translation de vecteur est une transformation qui, à tout point M, associe le point M' tel que:

On dit alors que M’ est le translaté de M.

Une translation de vecteur 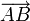transforme le point M en un point M' tel que ABM'M soit un parallélogramme.

Géométrie « classique »

En géométrie plane et en géométrie dans l’espace, une translation se traduit par un déplacement de toute la figure sans changement ni de la direction, ni du sens, ni des longueurs.

Construire l'image d'une figure par une translation revient à la faire glisser dans une direction, un sens et avec une longueur donnée.

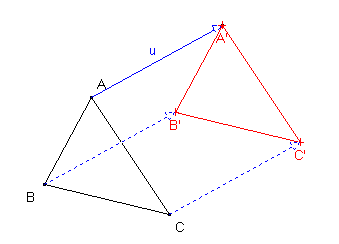
Conservation : Un tel glissement n'entraîne pas de déformation ni de changement de disposition, donc:

Dans une translation, les longueurs, le parallélisme, la perpendicularité et plus généralement les angles sont conservés.

Une translation transforme une droite en une droite parallèle.

Par une translation, une figure géométrique est transformée en une figure géométrique semblable.

Pour construire l'image d'une figure géométrique, on ne construit donc que l'image de ses points caractéristiques: pour un segment, ses extrémités, pour un triangle, ses trois sommets, pour un cercle, son centre et son rayon, etc.

La translation est la seule transformation qui laisse invariant les vecteurs c’est-à-dire telle que

La composée de deux translations de vecteur et est une translation de vecteur 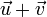. La translation de vecteur nul est l’identité. Ces propriétés confèrent à l’ensemble des translations muni de la loi de composition un statut de groupe commutatif isomorphe à l’ensemble des vecteurs du plan ou de l’espace.

Ce groupe est un sous-groupe du groupe des déplacements, du groupe des homothéties-translation, du groupe des symétries-translation, du groupe des rotations-translation.

Généralisation à un espace affine

On définit de même une translation dans un espace affine quelconque comme la transformation qui, à tout point M associe le point M’ tel que

Expressions d’une translation

Coordonnées cartésiennes

Dans le plan, la translation de vecteur 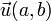, transforme le point M(x , y) en M'(x' , y') tel que

x' = x + a

y' = y + b

Dans l’espace, la translation de vecteur 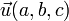, transforme le point M(x , y, z) en M'(x' , y', z') tel que

x' = x + a

y' = y + b

z' = z + c

Plus généralement, dans un espace de dimension n, la translation de vecteur de coordonnées , transforme le point en tel que

x'_i = x_i + a_i pour tout i de i = 1 à n

Expression complexe

Dans le plan complexe, la translation de vecteur d'affixe a (a complexe), transforme le point M(z) en M'(z') tel que

z' = z + a

Coordonnées homogènes

En travaillant avec les coordonnées homogènes, on peut définir une matrice de translation :

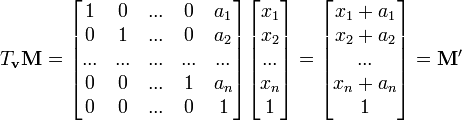
Dans un espace affine de dimension n, la matrice de translation de vecteur est une matrice de dimension n+1 définie par :

L'écriture de la translation devient alors

Cette écriture permet de créer un isomorphisme entre les matrices n+1 de cette forme et l'ensemble des translations dans un espace de dimension n.

L'inverse d'une telle matrice s'obtient en changeant la direction du vecteur:

De même, le produit des matrices revient à faire une somme de vecteurs:

Et puisque l'addition des vecteurs est commutative, le groupe multiplicatif de matrices ainsi créé est un groupe commutatif.

• Portail de la géométrie