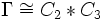Transformation modulaire

En mathématiques, on appelle groupe modulaire le groupe quotient de SL(2,ℤ) par son centre {Id, -Id}, souvent noté Γ(1), ou même tout simplement Γ. Il convient de l'identifier avec l'image de SL(2,ℤ) dans le groupe de Lie PGL(2,ℝ).

Sommaire 1 Action sur le demi-plan de Poincaré 2 La Courbe modulaire 3 Présentation du groupe modulaire 4 Références externes

Action sur le demi-plan de Poincaré

Ce nom provient de l'action à gauche et fidèle de Γ(1) par homographies sur le demi-plan de Poincaré 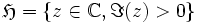des nombres complexes de partie imaginaire strictement positive.

Cette action n'est que la restriction de l'action de PGL(2,ℂ) sur la droite projective complexe 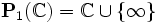: La matrice 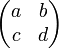agit sur 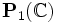en envoyant z sur 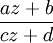. En coordonnées homogènes, [z:t] est envoyé sur [az+bt:cz+dt].

Comme le groupe PGL(2,ℝ) stabilise la droite projective réelle de , ce groupe stabilise aussi le complémentaire. Comme PGL(2,ℝ) est en outre connexe, il stabilise également chacune des deux composantes de 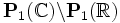, en particulier 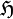. Il en est donc de même du sous-groupe modulaire Γ(1).

La Courbe modulaire

Le quotient du demi-plan de Poincaré par le groupe modulaire donne lieu à une surface de Riemann 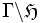(«Gamma sous H»), souvent notée, ce qui selon les conventions peut être considéré un abus de notation, 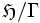(«H sur Gamma»).

Cette surface de Riemann est souvent dénommée courbe modulaire, car elle paramètre les classes d'isomorphismes de courbes elliptiques complexes. Mieux, la courbe modulaire est la droite complexe ℂ. À chaque courbe elliptique complexe E correspond un nombre complexe, son j-invariant, noté j(E) ou j_E. Ce nombre caractérise la courbe elliptique E à isomorphisme près. On dit que c'est son module.

À tout point τ du demi-plan de Poincaré on associe le tore quotient 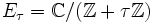. C'est une courbe elliptique. On peut donc considérer son module j(E_τ). On obtient ainsi une fonction à valeurs complexes définie sur 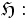c'est la fonction j. C'est une fonction holomorphe sur 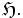Comme E_τ ne dépend que du réseau 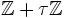, la fonction est constantes sur les orbites de Γ: on dit qu'elle commute à l'action de Γ. Ainsi la fonction j induit par passage au quotient une application 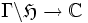. Cette application est bijective et biholomorphe, ce qui justifie le nom de courbe modulaire donné au quotient .

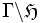Présentation du groupe modulaire

Le groupe modulaire est engendré par les deux transformations

S: 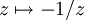et T: .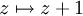

Autrement dit, tout élément du groupe modulaire s'obtient en composant S et T. Cette écriture n'est pas unique. En effet les générateurs S et T vérifient les relations

S² = 1 et (ST)³ = 1,

ce qui donne deux écriture distinctes de 1, la transformation identique. En fait les deux relations ci dessus engendrent toutes les relations entre S et T. On dit alors que l'on a une présentation du groupe modulaire, donnée par générateurs et relations, ce que l'on résume par la formule

.

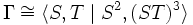Notons U le produit ST, qui agit par 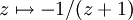. La formule ci-dessus revient aussi à dire que tout élément de Γ s'écrit, et ce de manière unique, comme produit de S, U et U², où les facteurs U et U² sont toujours séparés par des facteurs S. On dit encore que le groupe modulaire est le produit libre du sous-groupe engendré par S (isomorphe au groupe cyclique C₂ d'ordre 2) par le sous-groupe engendré par U (isomorphe au groupe cyclique C₃ d'ordre 3).

En termes géométriques,

S agit par l'inversion par rapport au cercle unité, suivie par la réflexion par rapport à la droite Re(z)=0 et

T agit par la translation d'une unité vers la droite.

Références externes

• Groupe modulaire, fractions continues et approximation

• Portail des mathématiques