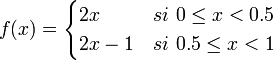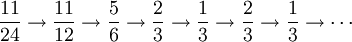- Transformation dyadique
-
Décalage de Bernoulli (mathématiques)
 Pour les articles homonymes, voir Décalage de Bernoulli.
Pour les articles homonymes, voir Décalage de Bernoulli.
Le décalage de Bernoulli (également connu comme fonction dyadique ou fonction 2x mod 1) est l'application
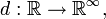 produite par la règle
produite par la règle 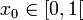 et
et 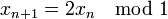 quel que soit n ≥ 0.
quel que soit n ≥ 0.De façon équivalente, le décalage de Bernoulli peut également être défini comme la fonction itérée de la fonction affine par parties
Le décalage de Bernoulli fournit un exemple de la manière dont une simple fonction unidimensionelle peut mener au chaos.
Si x0 est rationnel, l'image de x0 contient un nombre fini de valeurs différentes dans [0, 1[ et l'orbite positive de x0 est périodique à partir d'un certain point, avec la même période que le développement binaire de x0. Par exemple, l'orbite positive de 11/24 est :
Si x0 est irrationnel, l'image de x0 contient un nombre infini de valeurs différentes et l'orbite positive de x0 n'est jamais périodique.
À l'intérieur de n'importe quel sous-intervalle de [0,1[, aussi petit qu'il soit, il y a donc une infinité de points dont les orbites sont périodiques à partir d'un certain point et un nombre infini de points dont les orbites ne sont jamais périodiques. Cette sensibilité extrême aux conditions initiales est une caractéristique des fonctions chaotiques.
Le décalage de Bernoulli est le conjugué topologique de la fonction en tente de hauteur unité.
Intégrabilité
Le décalage de Bernoulli est un modèle complètement intégrable dans la théorie du chaos déterministe. Les fonctions propres de carré sommable de l'opérateur d'évolution associé au décalage de Bernouilli sont les polynômes de Bernoulli. Ces fonctions propres forment un spectre discret avec comme valeurs propres 2 − n pour les entiers non négatifs n.
Il existe des vecteurs propres plus généraux, qui ne sont pas de carré sommable, associés à un spectre continu. Ceux-ci sont donné par la fonction zêta d'Hurwitz ; de manière équivalente, les combinaisons de la fonction zêta d'Hurwitz donnent des fonctions propres dérivables nulle part, dont la fonction de Takagi. Les fonctions propres fractales présentent une symétrie par rapport au groupoïde du groupe modulaire.
Articles liés
Références
- Dean J. Driebe, Fully Chaotic Maps and Broken Time Symmetry, (1999) Kluwer Academic Publishers, Dordrecht Netherlands ISBN 0-7923-5564-4
- Linas Vepstas, The Bernoulli Map, the Gauss-Kuzmin-Wirsing Operator and the Riemann Zeta, (2004)
- Portail des mathématiques
Catégorie : Théorie du chaos
Wikimedia Foundation. 2010.

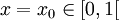 est
est