Tores maximaux

Dans la théorie de Lie, un tore maximal d'un groupe de Lie G est un sous-groupe de Lie commutatif, connexe et compact de G qui soit maximal pour ces propriétés. Les tores maximaux de G sont uniques à conjugaison près. De manière équivalente, c'est un sous-groupe de Lie de G, isomorphe à un tore, et maximal pour cette propriété. Le quotient du normalisateur N(T) d'un tore T par T est le groupe de Weyl associé.

Sommaire 1 Définition 2 Groupes de Lie compact 2.1 Propriétés 2.2 Groupe de Weyl 3 Groupe de Lie semi-simples

Définition

Tout groupe de Lie commutatif connexe est isomorphe à un quotient de Rⁿ par un sous-réseau. La commutativité et la connexité impliquent en effet que l'exponentielle g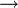G est un morphisme surjectif de groupes de Lie, dont le noyau est un sous-groupe additif discret de g. De suite, tout groupe de Lie commutatif connexe et compact est isomorphe au quotient de Rⁿ par un réseau, donc à un tore Tⁿ.

Un tore maximal d'un groupe de Lie G est par définition un sous-groupe fermé commutatif et connexe maximal, ou encore un sous-groupe de Lie isomorphe à un tore Tⁿ.

Les sous-groupes de Lie connexes de G sont exactement déterminés par les sous-algèbres de Lie de g. Dans cette correspondance biunivoque, les sous-groupes connexes et commutatifs correspondent aux sous-algèbres commutatives de g. En particulier, dans un groupe de Lie, tout sous-groupe compact commutatif connexe est inclus dans un tore maximal.

Les considérations sur les tores maximaux a son importance en particulier dans l'étude des resprésentations d'un groupe de Lie. En effet, il est facile d'obtenir la classification des représentations d'un tore.

Groupes de Lie compact

Dans un groupe de Lie compact, l'application exponentielle est surjective. En particulier, tout élément de G appartient à l'image d'un sous-groupe à un paramètre de G. L'adhérence de cette image est un sous-groupe fermé commutatif de G, donc inclus dans un tore maximal de G. De fait :

• Tout élément d'un groupe de Lie compact appartient à un tore maximal.

Propriétés

Tous les tores maximaux de G sont conjugués et en particulier ont même dimension k, appelée le rang du groupe de Lie G.

• Tout tore maximal est égal à son centralisateur.

Si un élément g commute avec tous les éléments d'un tore maximal T de G, le centralisateur C de g est un sous-groupe de Lie de G, contenant par choix de g le tore T. Il est clair que T est un tore maximal de C. L'élément g de C appartient à un tore maximal de C, donc est conjugué dans C à un élément de T. Comme g est dans le centre de C, g appartient à T. D'où le résultat.

• L'intersection des tores maximaux de G est exactement le centre de G.

Comme tout élément de G appartient à au moins un tore maximal, le centre de G est égal à l'intersection des centralisateurs des tores maximaux de G. Or, le centralisateur d'un tore maximal est lui-même ; le résultat en découle.

Groupe de Weyl

Le normalisateur de T (dans G) est un sous-groupe fermé de G, et de fait, par le théorème de Cartan un sous-groupe de Lie de G. Le groupe de Weyl W(T) assocé à T est le quotient du normalisateur de T dans G par T. Il s'avère que T est la composante neutre de son normalisateur. De manière équivalente, W(T) est un groupe fini.

Groupe de Lie semi-simples

Le rang d'un groupe de Lie semi-simple est égal au nombre de noeuds du diagramme de Dynkin associé.