- Demi-plan
-
La droite d partage le plan en deux demi-plans, l'un contenant M et N l'autre contenant P.
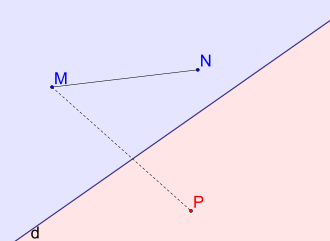
En géométrie affine plane, une droite partage un plan en deux demi-plans. Cette droite s'appelle alors la frontière des demi-plans.
Deux points M et N non situés sur la droite (d) sont situés dans le même demi-plan de frontière (d) si et seulement si le segment [MN] ne rencontre pas la droite (d). Et les points sont situés dans des demi-plans différents si et seulement si le segment [MN] rencontre la droite (d)[1].
Le demi-plan est un exemple simple d'ensemble convexe.
Sommaire
Intersections et unions
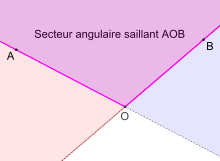
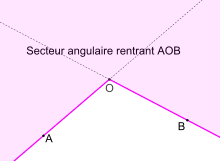
L'intersection de deux demi-plans dont les frontières sont des droites secantes en O donne un secteur angulaire saillant de sommet O. La réunion de ces mêmes demi-plans donne un secteur angulaire rentrant. Si les droites sont parallèles, qu'aucun des demi-plans n'est inclus dans l'autre, que l'intersection n'est pas vide, l'intersection des demi-plans donne une bande.
secteur angulaire saillant, intersection de deux demi-plans.
Secteur angulaire rentant, union de deux demi-plans.
Bande, intersection de deux demi-plans de frontières parallèles.Convexité
En tant qu'ensemble convexe simple, le demi-plan permet de caractériser des ensembles convexes plans.
Un polygone est convexe si et seulement si, quel que soit le côté que l'on choisit, le polygone est entièrement inclus dans un demi-plan dont la frontière porte ce côté. La portion de plan qu'il délimite est alors obtenue comme intersection des demi-plans dont les frontières sont les droites supportant ses côtés.
Enfin, un théorème de séparation permet d'affirmer que deux ensembles convexes disjoints d'un plan peuvent être séparés par une droite qui place chacun des deux ensembles dans des demi-plans différents.
Caractérisation par une inégalité
Lorsque le plan est muni d'un repère ou d'une distance, un demi-plan est caractérisé par une inéquation lié à l'équation de la droite (d). Une inégalité large correspond à un demi-plan fermé (contenant sa frontière) et une inégalité stricte à un demi-plan ouvert (ne contenant pas sa frontière).
Médiatrice
La médiatrice d'un segment [AB] où A et B sont deux points distincts est l'ensemble des points à égale distance de A et B, c'est donc l'ensemble des points M tels que MA = MB. Cette médiatrice partage le plan en deux demi-plans, l'un contenant A et tous les points qui sont plus proches de A que de B, ensemble des points M tels que MA < MB et l'autre, contenant B, correspondant à l'ensemble des points M tels que MA > MB.
Coordonnées cartésiennes
Si la droite (d) a pour équation ax+by+c=0, les deux demi-plans ouverts ont pour inéquations ax + by + c < 0 et ax + by + c > 0 et les demi-plans fermés par ax + by + c ≤ 0 et ax + by + c ≥ 0. Cette caractérisation du demi-plan permet de démontrer facilement qu'un demi-plan est convexe, que le segment reliant deux points dans des demi-plans différents coupe la frontière et qu'une demi-droite d'origine un point de la frontière et passant par un point d'un demi-plan est entièrement incluse dans ce demi-plan[2].
Si la droite a pour équation y = mx + p, le demi-plan d'inéquation y < mx + p est appelé demi-plan sous la droite (d) et le demi-plan d'inéquation y > mx+p est appelé demi-plan au-dessus de la droite (d).
Plan euclidien orienté
Dans un plan euclidien orienté, si une droite est orientée par un vecteur u et passe par A, on distingue deux demi-plans, l'un situé à droite de (d), ensemble des points P tels que l'angle (u, AP) soit de sinus négatif appelé demi-plan négatif , l'autre situé à gauche de (d) ensemble des points P tels que l'angle (u, AP) soit de sinus positif appelé demi-plan positif[3].
En coordonnées polaires, si la droite ne passe pas par l'origine et si son équation polaire est
- rcos(θ − φ0) = r0 où (r;θ) sont les coordonnées polaires de M et (r0;φ0) sont les coordonnées polaires du projeté orthogonal de O sur (d).
alors le demi-plan ne contenant pas l'origine est caractérisé par l'inéquation
- rcos(θ − φ0) > r0
Si la droite passe par l'origine et a pour vecteur directeur u de coordonnées polaires (1;α0), le demi-plan positif vérifie
- sin(θ − α0) > 0
Barycentre
Si A, B, et C sont trois points non alignés et si G est le barycentre du système pondéré {(A,a), (B,b), C(c)}, la position de G par rapport à la droite (AB) est déterminée par les signes comparés de c et a+b+c. Si c et a + b + c sont de même signe alors G est dans le demi-plan de frontière (AB) contenant C, si c et a+b+c sont de signes contraires, le point G est dans l'autre demi-plan.
Cette caractérisation permet de définir l'intérieur d'un triangle comme l'ensemble des barycentres des sommets affectés de poids de même signe.
Notes et références
- Voir, par exemple, Küstner, Hellwitch, Kästner, Petite encyclopédie des mathématiques, Édition Didier, 1980, ch 41, p 780, définition 2.
- Voir par exemple Dany-Jack Mercier, 'Demi-plan, convexité et Polynomes, IUFM de Guadeloupe, chap 2.
- Voir, par exemple, Küstner, Hellwitch, Kästner, Petite encyclopédie des mathématiques, Édition Didier, 1980, ch 13.2, p 313.
Voir aussi
Catégories :- Figure de géométrie
- Géométrie classique
Wikimedia Foundation. 2010.
