Théorème de représentation de riemann
- Théorème de représentation de riemann
-
Théorème de représentation de Riemann
Le théorème de la représentation conforme de Riemann classifie les parties simplement connexes de  .
.
Enoncé
Soit Ω un ouvert de  , distinct de
, distinct de  et simplement connexe. Alors il existe une fonction f holomorphe sur Ω, bijective, dont la réciproque est holomorphe, telle que f(Ω) = D(0,1), où D(0,1) est le disque de centre 0 et de rayon 1. De plus, pour
et simplement connexe. Alors il existe une fonction f holomorphe sur Ω, bijective, dont la réciproque est holomorphe, telle que f(Ω) = D(0,1), où D(0,1) est le disque de centre 0 et de rayon 1. De plus, pour 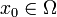 , on peut imposer que f(x0) = 0 et que f'(x0) > 0, auquel cas f est l'unique application qui fait l'affaire.
, on peut imposer que f(x0) = 0 et que f'(x0) > 0, auquel cas f est l'unique application qui fait l'affaire.
Notes et références de l'article
Voir aussi
Articles connexes
Liens et documents externes
 Portail des mathématiques
Portail des mathématiques
Catégories : Analyse complexe | Théorème de mathématiques | Bernhard Riemann
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de représentation de riemann de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Theoreme de representation de Riemann — Théorème de représentation de Riemann Le théorème de la représentation conforme de Riemann classifie les parties simplement connexes de . Sommaire 1 Enoncé 2 Notes et références de l article 3 Voir aussi … Wikipédia en Français
Théorème de représentation de Riemann — Le théorème de la représentation conforme de Riemann classifie les parties simplement connexes de . Sommaire 1 Enoncé 2 Notes et références de l article 3 Voir aussi … Wikipédia en Français
Theoreme de rearrangement de Riemann — Théorème de réarrangement de Riemann En mathématiques, le théorème de réarrangement de Riemann est un théorème, nommé en l honneur du mathématicien Bernhard Riemann, d après lequel si une série à valeurs réelles est semi convergente, alors on… … Wikipédia en Français
Théorème de réarrangement de Riemann — En mathématiques, le théorème de réarrangement de Riemann est un théorème, nommé en l honneur du mathématicien Bernhard Riemann, d après lequel si une série à valeurs réelles est semi convergente, alors on peut réarranger ses termes pour qu elle… … Wikipédia en Français
Theoreme de representation de Riesz — Théorème de représentation de Riesz Il existe en analyse fonctionnelle plusieurs théorèmes nommés théorème de représentation de Riesz, en l honneur du mathématicien Frigyes Riesz. Sommaire 1 Le théorème de représentation de Riesz dans les espaces … Wikipédia en Français
Théorème de représentation de riesz — Il existe en analyse fonctionnelle plusieurs théorèmes nommés théorème de représentation de Riesz, en l honneur du mathématicien Frigyes Riesz. Sommaire 1 Le théorème de représentation de Riesz dans les espaces de Hilbert 1.1 Énoncé 1.2 … Wikipédia en Français
Théorème de représentation de Riesz — Pour les articles homonymes, voir Théorème de Riesz. Il existe en analyse fonctionnelle plusieurs théorèmes nommés théorème de représentation de Riesz, en l honneur du mathématicien Frigyes Riesz. Sommaire 1 Le théorème de représentation de Riesz … Wikipédia en Français
Théorème de tsuji — Le théorème de Masatsugu Tsuji est un équivalent du théorème de représentation de Riemann en connectivité 2. Il peut s énoncer de la façon suivante : Soit K un ensemble connexe et relativement compact dans . Si l on note la frontière… … Wikipédia en Français
Théorème de Tsuji — En analyse complexe, le théorème de Masatsugu Tsuji est un équivalent du théorème de représentation de Riemann en connectivité 2. Il peut s énoncer de la façon suivante : Théorème de Masatsugu Tsuji Soit K un ensemble connexe et… … Wikipédia en Français
RIEMANN (B.) — Après la mort de Georg Friedrich Bernhard Riemann, son œuvre fut publiée en un seul volume, y compris les fragments posthumes, et cette brièveté ne tient pas seulement à la fin précoce du mathématicien: d’une part, ses démonstrations sont très… … Encyclopédie Universelle
 .
. , distinct de
, distinct de  et simplement connexe. Alors il existe une fonction f holomorphe sur Ω, bijective, dont la réciproque est holomorphe, telle que f(Ω) = D(0,1), où D(0,1) est le disque de centre 0 et de rayon 1. De plus, pour
et simplement connexe. Alors il existe une fonction f holomorphe sur Ω, bijective, dont la réciproque est holomorphe, telle que f(Ω) = D(0,1), où D(0,1) est le disque de centre 0 et de rayon 1. De plus, pour 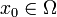 , on peut imposer que f(x0) = 0 et que f'(x0) > 0, auquel cas f est l'unique application qui fait l'affaire.
, on peut imposer que f(x0) = 0 et que f'(x0) > 0, auquel cas f est l'unique application qui fait l'affaire.