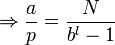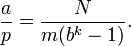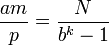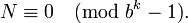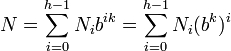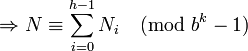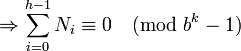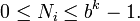- Théorème de midy
-
Théorème de Midy
En mathématiques, le Théorème de Midy, appelé ainsi en hommage au mathématicien français E. Midy[1], est un énoncé concernant le développement décimal des fractions a/p avec p un nombre premier et a/p est le développement en décimale récurrente avec une période paire. Si la période de la représentation décimale de a/p est 2n, alors
et les chiffres dans le deuxième moitié du développement périodique décimal period sont le complément par rapport à 9 des chiffres correspondants dans la première moitié. En d'autres mots :
- ai + ai + n = 9
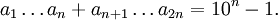
Par exemple
Sommaire
Théorème de Midy étendu
Si k est un diviseur quelconque de la période de l'expansion décimale de a/p (avec p encore premier) alors le Théoreme de Midy peut être généralisé de la maniere suivante. Le Théorème de Midy étendu[2] énonce que si une période de la representation décimale de a/p est divisé en blocs de taille k alors la somme de ces blocs est un multiple de 10k − 1. Qui plus est, si k vaut 2 ou 3, la somme des blocs vaut exactement 10k − 1.
Par exemple
a une période 18. En divisant une période en blocs de taille 6 ou 3 et en sommant, on trouve:
- 052631 + 578947 + 368421 = 999999
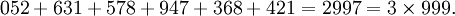
Théorème de Midy dans d'autres bases
Le théoreme de Midy et ses extensions ne dépendent pas de propriétés particulières de l'expansion décimale, car il marche encore dans n'importe quelle base b, a condition de remplacer 10k − 1 par bk − 1 et d'effectuer les opérations d'addition dans la base b. Par exemple, en octal
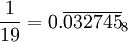
- 0328 + 7458 = 7778
- 038 + 278 + 458 = 778.
Preuve du Théorème de Midy
De courtes preuves peuvent être données en utilisant des résultats de la Theorie des groupes. Cependant, on peut aussi démontrer ce théoreme en utilisant l'algèbre élémentaire et l'arithmétique modulaire:
Soit p un nombre premier et a/p une fraction comprise entre 0 et 1. Supposons que l'expansion de a/p en base b soit de periode l, alors
ou N est l'entier dont l'écriture en base b est definie par la suite a1a2...al.
bl − 1 est un multiple de p parce que (bl−1)a/p est un entier. De plus, bn−1 n'est pas un multiple de p pour toutes les valeurs de n plus petite que l, car sinon la periode de l'expansion en base b de a/p serait plus petite que l.
Maintenant supposons que l=hk. Alors bl−1 est un multiple de bk − 1. Posons bl − 1 = m(bk − 1), alors
Mais bl−1 est un multiple de p; bk−1 n'est pas un multiple de p (car k est plus petit que l); et p est premier; donc m doit être un multiple de p et
est un entier. En d'autres mots:
Maintenant, découpons a1a2...al en h parts de taille egale a k, et posons que ces parts soient l'écriture en base b des entiers N0...Nh − 1, alors
![N_{h-1}=[a_1\dots a_k]_b](/pictures/frwiki/49/1dec65318d6e9496cd843fd1f842ba11.png)
![N_{h-2}=[a_{k+1}\dots a_2k]_b](/pictures/frwiki/54/6299d32397949fcf9b6b1b781025b998.png)
- .
- .
![N_0=[a_{l-k+1}\dots a_l]_b](/pictures/frwiki/99/cf52e72c42029c92a1ac7da1323f8bbf.png)
Pour demontrer le Théorème de Midy étendu en base b nous devons montrer que la somme des h entiers Ni est un multiple de bk − 1.
Comme bk est congru a 1 modulo bk−1, n'importe quelle puissance de bk sera aussi congru a 1 modulo bk − 1. donc
ce qui prouve Théorème de Midy étendu en base b.
Pour prouver le théorème de Midy original, il suffit de prendre la cas particulier où h = 2. N0 et N1 sont tous les 2 représentés par une séquence de k chiffres en base b, donc ils satisfont tous 2
N0 et N1 ne peuvent pas tous 2 être nuls (sinon a/p = 0) et ne peuvent pas tous 2 être egal a bk − 1 (sinon a/p = 1), donc
- 0 < N0 + N1 < 2(bk − 1)
et comme N0 + N1 est un multiple de bk − 1, il vient que
- N0 + N1 = bk − 1.
Références
- ↑ A Theorem on Repeating Decimals; W. G. Leavitt; American Mathematical Monthly, Vol. 74, No. 6 (Jun. - Jul., 1967) , pp. 669-673
- ↑ Extended Midy's Theorem, Bassam Abdul-Baki, 2005
Liens externes
- Portail des mathématiques
Catégories : Théorème de mathématiques | Fraction | Arithmétique
Wikimedia Foundation. 2010.

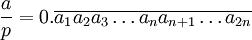
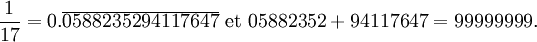
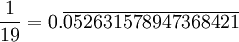
![\frac{a}{p}=[0.\overline{a_1a_2\dots a_l}]_b](/pictures/frwiki/100/d59c45cb541c04a300cab2cf4784986c.png)
![\Rightarrow\frac{a}{p}b^l=[a_1a_2\dots a_l.\overline{a_1a_2\dots a_l}]_b](/pictures/frwiki/53/55e4ec06bd7c5c2b83146794911af570.png)
![\Rightarrow\frac{a}{p}b^l=N+[0.\overline{a_1a_2\dots a_l}]_b=N+\frac{a}{p}](/pictures/frwiki/56/8cfc5f91cf394b9a517c986cc1171cd1.png)