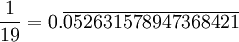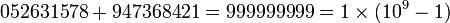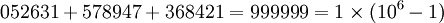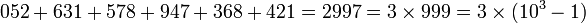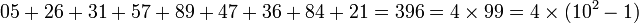052631578947368421

052 631 578 947 368 421 est un nombre cyclique, c'est-à-dire que ses multiples sont obtenus par permutations circulaires des chiffres de ce nombre. Sa particularité est de se former d'une façon très simple.

Obtention du nombre

On écrit d'abord l'unité: 1

Puis on la multiplie par deux, et on inscrit le résultat à sa droite de l'unité

On recommence à chaque fois le calcul et on écrit toujours le résultat à droite. Attention de ne pas oublier les retenues.

Etape	Ce que l'on fait	Calcul	Retenu	Résultat	Avancement
1	On écrit d'abord l'unité:	1	--	1	1
2	Puis on multiplie 1 par deux	1 x 2 = 1	--	2	21
3	On multiplie 2 par deux	2 x 2 = 4	--	4	421
4	On multiplie 4 par deux	4 x 2 = 8	--	8	8421
5	On multiplie 8 par deux	8 x 2 = 16	1	6	68421
6	On multiplie 6 par deux plus la retenu	6 x 2 + 1 = 13	1	3	368421
7	On multiplie 3 par deux plus la retenu	3 x 2 + 1 = 7	--	7	7368421
8	On multiplie 7 par deux	7 x 2 = 14	1	4	47368421
9	On multiplie 4 par deux plus la retenu	4 x 2 + 1 = 9	--	9	947368421
10	On multiplie 9 par deux	9 x 2 = 18	1	8	8947368421
11	On multiplie 8 par deux plus la retenu	8 x 2 + 1 = 17	1	7	78947368421
12	On multiplie 7 par deux plus la retenu	7 x 2 + 1 = 15	1	5	578947368421
13	On multiplie 5 par deux plus la retenu	5 x 2 + 1 = 11	1	1	1578947368421
14	On multiplie 1 par deux plus la retenu	1 x 2 + 1 = 3	--	3	31578947368421
15	On multiplie 3 par deux	3 x 2 = 6	--	6	631578947368421
16	On multiplie 6 par deux	6 x 2 = 12	1	2	2631578947368421
17	On multiplie 2 par deux plus la retenu	2 x 2 + 1 = 5	--	5	52631578947368421
18	On rajoute un zéro	0	--	0	052631578947368421

Propriétés

A part 9 et 0, tous les chiffres sont présents deux fois dans le nombre.

Les nombres cycliques sont liés aux décimales récurrentes des fractions unitaires.

Ainsi:

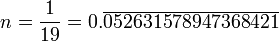
$n=\frac{1}{19}=0.\overline{052631578947368421}$

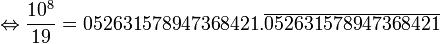
$\Leftrightarrow\frac{10^8}{19}=052631578947368421.\overline{052631578947368421}$

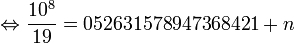
$\Leftrightarrow\frac{10^8}{19}=052631578947368421+n$

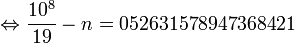
$\Leftrightarrow\frac{10^8}{19}-n=052631578947368421$

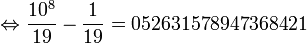
$\Leftrightarrow\frac{10^8}{19}-\frac{1}{19}=052631578947368421$

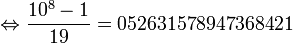
$\Leftrightarrow\frac{10^8-1}{19}=052631578947368421$

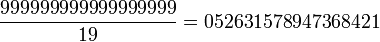
et l'on trouve $\frac{999999999999999999}{19}=052631578947368421$

Et comme 19 est un nombre premier, il répond au théorème de Midy et au Théorème de Midy étendu:

$\frac{1}{19}=0.\overline{052631578947368421}$

En divisant une période en blocs de taille 9 ou 6 ou 3 ou 2 et en sommant, on trouve:

$052631578+947368421=999999999= 1\times(10^9-1)$

$052631+578947+368421=999999= 1\times(10^6-1)$

$052+631+578+947+368+421=2997=3\times999= 3\times (10^3-1)$

$05+26+31+57+89+47+36+84+21=396=4\times99= 4\times (10^2-1)$

Multiples

La rang donné est l'endroit où il faut commencer à lire le nombre originel pour obtenir son multiple, ceci en partant de la fin du nombre.

n	n / 19 =	n × 052631578947368421	Rang de début de lecture
1	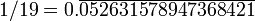$1 / 19 = 0.\overline{052631578947368421}$	052 631 578 947 368 421	18
2	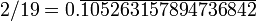$2 / 19 = 0.\overline{105263157894736842}$	105 263 157 894 736 842	1
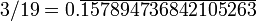
3	$3 / 19 = 0.\overline{157894736842105263}$	1 578 947 368 42105 263	13
4	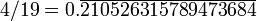$4 / 19 = 0.\overline{210526315789473684}$	210526 315 789 473 684	2
5	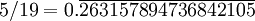$5 / 19 = 0.\overline{263157894736842105}$	2 631 578 947 368 42105	16
6	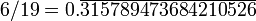$6 / 19 = 0.\overline{315789473684210526}$	31 578 947 368 4210526	14
7	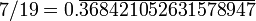$7 / 19 = 0.\overline{368421052631578947}$	368 421052 631 578 947	6
8	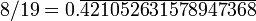$8 / 19 = 0.\overline{421052631578947368}$	421052 631 578 947 368	3
9	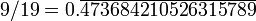$9 / 19 = 0.\overline{473684210526315789}$	47 368 4210526 315 789	8
10	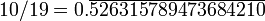$10 / 19 = 0.\overline{526315789473684210}$	52 631 578 947 368 4210	17
11	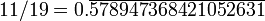$11 / 19 = 0.\overline{578947368421052631}$	578 947 368 421052 631	12
12	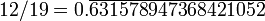$12 / 19 = 0.\overline{631578947368421052}$	631 578 947 368 421052	15
13	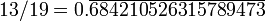$13 / 19 = 0.\overline{684210526315789473}$	68 4210526 315 789 473	5
14	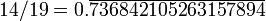$14 / 19 = 0.\overline{736842105263157894}$	7 368 42105 263 157 894	7
15	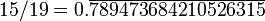$15 / 19 = 0.\overline{789473684210526315}$	78 947 368 4210526 315	11
16	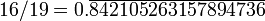$16 / 19 = 0.\overline{842105263157894736}$	8 42105 263 157 894 736	4
17	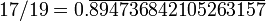$17 / 19 = 0.\overline{894736842105263157}$	8 947 368 42105 263 157	10
18	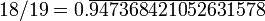$18 / 19 = 0.\overline{947368421052631578}$	947 368 421052 631 578	9
19	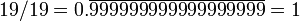$19 / 19 = 0.\overline{999999999999999999} = 1$	999 999 999 999 999 999	--

Portail des mathématiques

Ce document provient de « 052631578947368421 ».

Catégorie : Nombre

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article 052631578947368421 de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Duodecimal — For the similar sounding classification system, see Dewey Decimal Classification. Numeral systems by culture Hindu Arabic numerals Western Arabic (Hindu numerals) Eastern Arabic Indian family Tamil Burmese Khmer Lao Mongolian Thai East Asian… … Wikipedia
Swami Bharati Krishna Tirtha's Vedic mathematics — For the actual mathematics of the Vedic period, see the articles on Sulba Sūtras and Indian mathematics.Swami Bharati Krishna Tirtha s Vedic mathematics is a system of mathematics consisting of a list of 16 basic sūtras, or aphorisms. They were… … Wikipedia
Cyclic number — This article is about numbers where permutations of their digits (in some base) yield related numbers. For the number theoretic concept, see cyclic number (group theory). A summary of this article appears in Repeating decimal. A cyclic number is… … Wikipedia
Midy's theorem — In mathematics, Midy s theorem, named after French mathematician E. Midy,[1] is a statement about the decimal expansion of fractions a/p where p is a prime and a/p has a repeating decimal expansion with an even period. If the period of the… … Wikipedia
Parasitic number — An n parasitic number (in base 10) is a positive natural number which can be multiplied by n by moving the rightmost digit of its decimal representation to the front. Here n is itself a single digit positive natural number. In other words, the… … Wikipedia
Repeating decimal — A decimal representation of a real number is called a repeating decimal (or recurring decimal) if at some point it becomes periodic: there is some finite sequence of digits that is repeated indefinitely. For example, the decimal representation of … Wikipedia
Decimale recurrente — Développement décimal périodique Premières décimales de quelques rationnels En mathématiques, le développement décimal périodique d un nombre rationnel est une écriture qui explicite la suite des décimales de … Wikipédia en Français
Décimale Récurrente — Développement décimal périodique Premières décimales de quelques rationnels En mathématiques, le développement décimal périodique d un nombre rationnel est une écriture qui explicite la suite des décimales de … Wikipédia en Français
Décimale récurrente — Développement décimal périodique Premières décimales de quelques rationnels En mathématiques, le développement décimal périodique d un nombre rationnel est une écriture qui explicite la suite des décimales de … Wikipédia en Français
Développement décimal périodique — Premières décimales de quelques rationnels En mathématiques, le développement décimal périodique d un nombre rationnel est une écriture qui explicite la suite des décimales de ce nombre, en indiquant un bloc de chiffres qui se répète à l infini.… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

052631578947368421