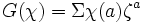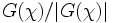Théorème de chowla-mordell
- Théorème de chowla-mordell
-
Théorème de Chowla-Mordell
En mathématiques, le théorème de Chowla-Mordell est un résultat de la théorie des nombres déterminant les cas où une somme de Gauss est la racine carrée d'un nombre premier, multipliée par une racine de l'unité. Il fut démontré et publié indépendamment par Sarvadaman Chowla et Louis Mordell, en 1951.
En détail, si p est un nombre premier, 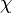 un caractère de Dirichlet modulo p, et
un caractère de Dirichlet modulo p, et
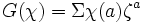
où 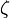 est une racine primitive p-ième de l'unité en nombres complexes, alors
est une racine primitive p-ième de l'unité en nombres complexes, alors
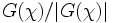
est une racine de l'unité si et seulement si 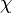 est le symbole de Legendre modulo p. Le premier « si » était connu de Gauss : la contribution de Chowla et Mordell fut la direction du « seulement si ». Le rapport dans le théorème apparaît dans l'équation fonctionnelle des fonctions L.
est le symbole de Legendre modulo p. Le premier « si » était connu de Gauss : la contribution de Chowla et Mordell fut la direction du « seulement si ». Le rapport dans le théorème apparaît dans l'équation fonctionnelle des fonctions L.
Référence
Gauss and Jacobi Sums par Bruce C. Berndt, Ronald J. Evans et Kenneth S. Williams, Wiley-Interscience, p.53.
 Portail des mathématiques
Portail des mathématiques
Catégories : Fonction zêta | Corps cyclotomiques | Théorème de mathématiques
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de chowla-mordell de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Theoreme de Chowla-Mordell — Théorème de Chowla Mordell En mathématiques, le théorème de Chowla Mordell est un résultat de la théorie des nombres déterminant les cas où une somme de Gauss est la racine carrée d un nombre premier, multipliée par une racine de l unité. Il fut… … Wikipédia en Français
Théorème de Chowla-Mordell — En mathématiques, le théorème de Chowla Mordell est un résultat de la théorie des nombres déterminant les cas où une somme de Gauss est la racine carrée d un nombre premier, multipliée par une racine de l unité. Il fut démontré et publié… … Wikipédia en Français
Louis Mordell — Louis Joel Mordell est un mathématicien américano britannique, né le 28 janvier 1888 à Philadelphie et mort le 12 mars 1972 à Cambridge. Pionnier par ses recherches en théorie des nombres, il est un spécialiste reconnu des équations… … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Liste Des Matières De La Théorie Des Nombres — Article détaillé : cryptologie. . Sommaire 1 Facteur (mathématiques) 2 Fractions 3 Arithmétique modulaire 4 … Wikipédia en Français
Liste des matieres de la theorie des nombres — Liste des matières de la théorie des nombres Article détaillé : cryptologie. . Sommaire 1 Facteur (mathématiques) 2 Fractions 3 Arithmétique modulaire 4 … Wikipédia en Français
Liste des matières de la théorie des nombres — Article détaillé : cryptologie. . Sommaire 1 Facteur (mathématiques) 2 Fractions 3 Arithmétique modulaire 4 Test de primalité e … Wikipédia en Français
Liste Des Théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème … Wikipédia en Français
Liste des theoremes — Liste des théorèmes Liste des théorèmes par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le… … Wikipédia en Français
Liste des théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème … Wikipédia en Français
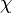 un caractère de Dirichlet modulo p, et
un caractère de Dirichlet modulo p, et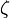 est une racine primitive p-ième de l'unité en nombres complexes, alors
est une racine primitive p-ième de l'unité en nombres complexes, alors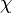 est le symbole de Legendre modulo p. Le premier « si » était connu de Gauss : la contribution de Chowla et Mordell fut la direction du « seulement si ». Le rapport dans le théorème apparaît dans l'équation fonctionnelle des fonctions L.
est le symbole de Legendre modulo p. Le premier « si » était connu de Gauss : la contribution de Chowla et Mordell fut la direction du « seulement si ». Le rapport dans le théorème apparaît dans l'équation fonctionnelle des fonctions L.