Théorème de Kennelly

Théorème de Kennelly: Présentation des montages sous forme de triangle (à gauche) et d'étoile (à droite).

Le théorème de Kennelly, ou transformation triangle-étoile, ou transformation Y-Δ, ou encore transformation T-Π, est une technique mathématique qui permet de simplifier l'étude de certains réseaux électriques.

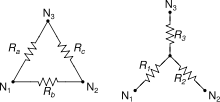
Ce théorème, nommé ainsi en hommage à Arthur Edwin Kennelly, permet de passer d'une configuration « triangle » (ou Δ, ou Π, selon la façon dont on dessine le schéma) à une configuration « étoile » (ou, de même, Y ou T). Le schéma ci-contre est dessiné sous la forme « triangle-étoile » ; les schémas ci-dessous sous la forme T-Π.

Ce théorème est utilisé en électrotechnique ou en électronique de puissance afin de simplifer des systèmes triphasés. Il est aussi d'utilisation courante en électronique pour simplifier le calcul de filtres ou d'atténuateurs.

Transformation étoile vers triangle

Tableau des formules de transformation ( étoile vers triangle )
Avec les impédances Avec les admittances

La somme des produits des impédances divisée par l'impédance opposée. Le produit des admittances adjacentes divisé par la somme totale des admittances.

$Z_{AB}=\frac{Z_{AT}.Z_{BT}+ Z_{BT}.Z_{CT}+Z_{CT}.Z_{AT}}{Z_{CT}}$

$Z_{BC}=\frac{Z_{AT}.Z_{BT}+ Z_{BT}.Z_{CT}+Z_{CT}.Z_{AT}}{Z_{AT}}$

$Z_{CA}=\frac{Z_{AT}.Z_{BT}+ Z_{BT}.Z_{CT}+Z_{CT}.Z_{AT}}{Z_{BT}}$
$Y_{AB}=\frac{Y_{AT} . Y_{BT}}{Y_{AT}+Y_{BT}+Y_{CT}}$

$Y_{BC}=\frac{Y_{BT} . Y_{CT}}{Y_{AT}+Y_{BT}+Y_{CT}}$

$Y_{CA}=\frac{Y_{CT} . Y_{AT}}{Y_{AT}+Y_{BT}+Y_{CT}}$

Démonstration

Cette démonstration peut être transposée à tous les énoncés du théorème.

Considérons le schéma précédent et utilisons le principe de superposition. On peut alors virtuellement annuler les potentiels en $B$ et $C$ , c'est-à-dire mettre ces points à la masse, dans les deux schémas. Calculons alors l'admittance équivalente entre le point $A$ et la masse, qui doit être identique dans les deux cas.

Schéma en étoile: $Y_{eq_1} =\frac{Y_{AT}.(Y_{BT}+Y_{CT})}{Y_{AT}+ Y_{BT} + Y_{CT}}$
Schéma en triangle: $Y_{eq_1} = Y_{AC} + Y_{AB}$
(Voir Impédance pour les détails de calcul) En répétant le calcul en éteignant successivement $V A$ et $V B$ puis $V A$ et $V C$ on obtient alors le système suivant:

$Y_{AB} + Y_{AC} = Y_{eq_1} (1)$
$Y_{AB} + Y_{BC} = Y_{eq_2} (2)$
$Y_{AC} + Y_{BC} = Y_{eq_3} (3)$

Soit en calculant membre à membre (1) + (2) - (3):

$Y_{AB} =\frac{Y_{eq_1}+ Y_{eq_2} - Y_{eq_3}}{2}$
$Y_{AB} =\frac{Y_{AT}.(Y_{BT}+Y_{CT}) + Y_{BT}.(Y_{AT}+Y_{CT}) - Y_{CT}.(Y_{AT}+Y_{BT})}{2.(Y_{AT}+Y_{BT}+Y_{CT})}$
$Y_{AB}=\frac{Y_{AT} . Y_{BT}}{Y_{AT}+Y_{BT}+Y_{CT}}$

De même (2) + (3) - (1) nous donne $Y B C$
et (1) + (3) - (2) nous donne $Y A C$

Transformation triangle vers étoile

On parle ici d'une équivalence d'un circuit en T avec un circuit en π. Dans la pratique, on utilise davantage la transformation qui consiste à passer d'un circuit en π à un circuit en T.

Tableau des formules de conversion ( triangle vers étoile )
Avec les impédances Avec les admitances

Le produit des impédances adjacentes divisé par la somme totale des impédances. La somme des produits des admittances divisée par l'admittance opposée.

$Z_{AT}=\frac{Z_{AB} . Z_{AC}}{Z_{AB}+Z_{BC}+Z_{AC}}$

$Z_{BT}=\frac{Z_{AB} . Z_{BC}}{Z_{AB}+Z_{BC}+Z_{AC}}$

$Z_{CT}=\frac{Z_{AC} . Z_{BC}}{Z_{AB}+Z_{BC}+Z_{AC}}$
$Y_{AT}=\frac{Y_{AB}.Y_{BC}+ Y_{CA}.Y_{AB}+Y_{BC}.Y_{CA}}{Y_{BC}}$

$Y_{BT}=\frac{Y_{AB}.Y_{BC}+ Y_{CA}.Y_{AB}+Y_{BC}.Y_{CA}}{Y_{CA}}$

$Y_{CT}=\frac{Y_{AB}.Y_{BC}+ Y_{CA}.Y_{AB}+Y_{BC}.Y_{CA}}{Y_{AB}}$

Voir aussi

Électricité

Électrocinétique

Quadripôle

Portail de la physique

Portail de l’électricité et de l’électronique

Catégories :
Théorie électrique
Théorème de physique

Tableau des formules de transformation ( étoile vers triangle )
Avec les impédances	Avec les admittances
La somme des produits des impédances divisée par l'impédance opposée.	Le produit des admittances adjacentes divisé par la somme totale des admittances.
$Z_{AB}=\frac{Z_{AT}.Z_{BT}+ Z_{BT}.Z_{CT}+Z_{CT}.Z_{AT}}{Z_{CT}}$ $Z_{BC}=\frac{Z_{AT}.Z_{BT}+ Z_{BT}.Z_{CT}+Z_{CT}.Z_{AT}}{Z_{AT}}$ $Z_{CA}=\frac{Z_{AT}.Z_{BT}+ Z_{BT}.Z_{CT}+Z_{CT}.Z_{AT}}{Z_{BT}}$	$Y_{AB}=\frac{Y_{AT} . Y_{BT}}{Y_{AT}+Y_{BT}+Y_{CT}}$ $Y_{BC}=\frac{Y_{BT} . Y_{CT}}{Y_{AT}+Y_{BT}+Y_{CT}}$ $Y_{CA}=\frac{Y_{CT} . Y_{AT}}{Y_{AT}+Y_{BT}+Y_{CT}}$

Tableau des formules de conversion ( triangle vers étoile )
Avec les impédances	Avec les admitances
Le produit des impédances adjacentes divisé par la somme totale des impédances.	La somme des produits des admittances divisée par l'admittance opposée.
$Z_{AT}=\frac{Z_{AB} . Z_{AC}}{Z_{AB}+Z_{BC}+Z_{AC}}$ $Z_{BT}=\frac{Z_{AB} . Z_{BC}}{Z_{AB}+Z_{BC}+Z_{AC}}$ $Z_{CT}=\frac{Z_{AC} . Z_{BC}}{Z_{AB}+Z_{BC}+Z_{AC}}$	$Y_{AT}=\frac{Y_{AB}.Y_{BC}+ Y_{CA}.Y_{AB}+Y_{BC}.Y_{CA}}{Y_{BC}}$ $Y_{BT}=\frac{Y_{AB}.Y_{BC}+ Y_{CA}.Y_{AB}+Y_{BC}.Y_{CA}}{Y_{CA}}$ $Y_{CT}=\frac{Y_{AB}.Y_{BC}+ Y_{CA}.Y_{AB}+Y_{BC}.Y_{CA}}{Y_{AB}}$

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de Kennelly de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

Theoreme de Kennelly — Théorème de Kennelly Présentation des montages sous forme de triangle (à gauche) et d étoile (à droite). Le théorème de Kennelly, ou transformation triangle étoile, ou transformation Y Δ, ou encore transformation T Π, est une technique… … Wikipédia en Français
Théorème de kennelly — Présentation des montages sous forme de triangle (à gauche) et d étoile (à droite). Le théorème de Kennelly, ou transformation triangle étoile, ou transformation Y Δ, ou encore transformation T Π, est une technique mathématique qui permet de… … Wikipédia en Français
Theoreme de Millman — Théorème de Millman Le théorème de Millman est une forme particulière de la loi des nœuds exprimée en termes de potentiel. Il est ainsi nommé en l honneur de l électronicien américain Jacob Millman. Sommaire 1 Énonciation 2 Exemple 3 Applications … Wikipédia en Français
Théorème de millman — Le théorème de Millman est une forme particulière de la loi des nœuds exprimée en termes de potentiel. Il est ainsi nommé en l honneur de l électronicien américain Jacob Millman. Sommaire 1 Énonciation 2 Exemple 3 Applications … Wikipédia en Français
Kennelly — Arthur Edwin Kennelly Arthur Edwin Kennelly, (17 décembre, 1861 18 juin, 1939), ingénieur en électricité américain, fils d un officier naval irlandais, né à Colaba près de Bombay, Inde, décédé à Boston, Massachusetts. Il est célèbre pour avoir… … Wikipédia en Français
Théorème de Robertson-Seymour — En mathématiques, et plus précisément en théorie des graphes, le théorème de Robertson–Seymour (parfois également appelé le théorème des mineurs, et connu, avant qu il soit démontré, sous le nom de conjecture de Wagner), est un théorème démontré… … Wikipédia en Français
Théorème de Millman — Le théorème de Millman est une forme particulière de la loi des nœuds exprimée en termes de potentiel. Il est ainsi nommé en l honneur de l électronicien américain Jacob Millman. Sommaire 1 Énoncé 2 Exemple 3 Applications … Wikipédia en Français
Arthur E. Kennelly — Arthur Edwin Kennelly Arthur Edwin Kennelly, (17 décembre, 1861 18 juin, 1939), ingénieur en électricité américain, fils d un officier naval irlandais, né à Colaba près de Bombay, Inde, décédé à Boston, Massachusetts. Il est célèbre pour avoir… … Wikipédia en Français
Arthur Kennelly — Arthur Edwin Kennelly Arthur Edwin Kennelly, (17 décembre, 1861 18 juin, 1939), ingénieur en électricité américain, fils d un officier naval irlandais, né à Colaba près de Bombay, Inde, décédé à Boston, Massachusetts. Il est célèbre pour avoir… … Wikipédia en Français
Arthur Edwin Kennelly — Arthur Edwin Kennelly, (17 décembre, 1861 18 juin, 1939), ingénieur en électricité américain, fils d un officier naval irlandais, né à Colaba près de Bombay, Inde, décédé à Boston, Massachusetts. Il est célèbre pour avoir découvert des propriétés … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Théorème de Kennelly

Transformation étoile vers triangle

Transformation triangle vers étoile

Voir aussi

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Théorème de Kennelly

Transformation étoile vers triangle

Transformation triangle vers étoile

Voir aussi

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link