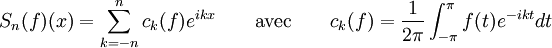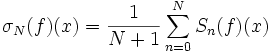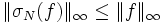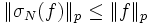Théorème de Fejér-Lebesgue
- Théorème de Fejér-Lebesgue
-
Théorème de Fejér
En mathématiques, le théorème de Fejér est un des principaux résultats de la théorie des séries de Fourier. Il donne des propriétés de convergence très générales pour la série de Fourier, dès lors qu'on utilise le procédé de sommation de Cesàro. Il a été démontré par le mathématicien Lipót Fejér en 1900[1].
Énoncé
Soit une fonction f 2π-périodique et localement intégrable. Alors on note
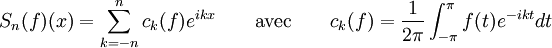
le terme d'ordre n de sa série de Fourier, et
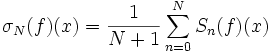
les moyennes de Cesàro successives des termes de la série de Fourier. On a alors les énoncés suivants :
- théorème de Fejér, version uniforme
- Si f est continue, la série de fonctions σN(f) converge uniformément vers la fonction f, avec en outre, pour tout N,
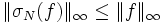
- théorème de Fejér, version Lp
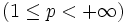 , aussi appelé théorème de Fejér-Lebesgue
, aussi appelé théorème de Fejér-Lebesgue
- Si f appartient à l'espace Lp, la série de fonctions σN(f) converge vers la fonction f au sens de la norme
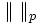 , avec en outre, pour tout N,
, avec en outre, pour tout N,
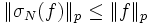
Applications
De très nombreux résultats concernant les séries de Fourier peuvent être obtenus comme conséquences du théorème de Fejér. dans les propositions suivantes, toutes les fonctions considérées sont 2π-périodiques.
- L'application qui à une fonction intégrable associe ses coefficients de Fourier est injective.
- L'injectivité est à comprendre dans l'espace L1, c'est-à-dire que deux fonctions ayant mêmes coefficients de Fourier sont égales presque partout. Dans le cas de deux fonctions continues, elles sont même égales.
De même le théorème de Fejér-Lebesgue apporte la preuve de la densité de l'espace des polynômes trigonométriques dans les différents espaces Lp.
- Si f est continue et si sa série de Fourier converge en un point x, alors elle converge nécessairement vers f(x).
- Ceci est à comparer au comportement de la série de Taylor d'une fonction, qui peut très bien, elle, converger vers une autre valeur que la valeur de la fonction.
- On peut utiliser le théorème de Fejér pour démontrer une version uniforme du théorème de Jordan-Dirichlet : si f est continue et à variation bornée, la série de Fourier de f converge uniformément vers f.
Notes et références
- ↑ Lipót Fejér, Sur les fonctions intégrables et bornées, C.R. Acad. Sci. Paris, 10 décembre 1900
 Portail des mathématiques
Portail des mathématiques
Catégories : Théorème de mathématiques | Série de Fourier
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de Fejér-Lebesgue de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Théorème de fejér — En mathématiques, le théorème de Fejér est un des principaux résultats de la théorie des séries de Fourier. Il donne des propriétés de convergence très générales pour la série de Fourier, dès lors qu on utilise le procédé de sommation de Cesàro.… … Wikipédia en Français
Théorème de Fejér — En mathématiques, le théorème de Fejér est un des principaux résultats de la théorie des séries de Fourier. Il donne des propriétés de convergence très générales pour la série de Fourier, dès lors qu on utilise le procédé de sommation de Cesàro.… … Wikipédia en Français
Théorème de Lebesgue — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. En mathématiques, plusieurs théorèmes portent, au moins en partie, le nom de Henri Léon Lebesgue : Théorèmes de convergence monotone et dominée de… … Wikipédia en Français
Théorèmes de Féjer — Théorème de Fejér En mathématiques, le théorème de Fejér est un des principaux résultats de la théorie des séries de Fourier. Il donne des propriétés de convergence très générales pour la série de Fourier, dès lors qu on utilise le procédé de… … Wikipédia en Français
LEBESGUE (H.) — Le mathématicien Henri Lebesgue est l’un des fondateurs de l’analyse moderne. Presque tous ses travaux se rattachent à la théorie des fonctions de variables réelles. Sa conception de l’intégration et de la mesure renouvelle l’étude des problèmes… … Encyclopédie Universelle
Coefficient de Fourier — Série de Fourier Le premier graphe donne l allure du graphe d une fonction périodique ; l histogramme donne les valeurs des modules des coefficients de Fourier correspondant aux différentes fréquences. En analyse, les séries de Fourier sont… … Wikipédia en Français
Coefficients de Fourier — Série de Fourier Le premier graphe donne l allure du graphe d une fonction périodique ; l histogramme donne les valeurs des modules des coefficients de Fourier correspondant aux différentes fréquences. En analyse, les séries de Fourier sont… … Wikipédia en Français
Décomposition d'un signal non sinusoïdal en séries de Fourier — Série de Fourier Le premier graphe donne l allure du graphe d une fonction périodique ; l histogramme donne les valeurs des modules des coefficients de Fourier correspondant aux différentes fréquences. En analyse, les séries de Fourier sont… … Wikipédia en Français
Définition et décomposition en série de Fourier d'un signal non sinusoidal — Série de Fourier Le premier graphe donne l allure du graphe d une fonction périodique ; l histogramme donne les valeurs des modules des coefficients de Fourier correspondant aux différentes fréquences. En analyse, les séries de Fourier sont… … Wikipédia en Français
Définition et décomposition en série de Fourier d'un signal non sinusoïdal — Série de Fourier Le premier graphe donne l allure du graphe d une fonction périodique ; l histogramme donne les valeurs des modules des coefficients de Fourier correspondant aux différentes fréquences. En analyse, les séries de Fourier sont… … Wikipédia en Français
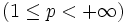 , aussi appelé théorème de Fejér-Lebesgue
, aussi appelé théorème de Fejér-Lebesgue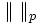 , avec en outre, pour tout N,
, avec en outre, pour tout N,