- Théorie mathématique sur le rubik's cube
-
Théorie mathématique sur le Rubik's Cube
Cet article présente le modèle mathématique relatif au Cube de Rubik.
Sommaire
Notations utilisées
 le groupe des mouvements légaux (sans démonter le cube !)
le groupe des mouvements légaux (sans démonter le cube !)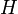 le groupe élargi (ici on peut faire sauter le cube)
le groupe élargi (ici on peut faire sauter le cube)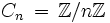
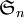 le groupe symétrique d'ordre n
le groupe symétrique d'ordre n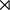 comme symbole pour le produit semi-direct
comme symbole pour le produit semi-direct pour la signature d'une permutation de
pour la signature d'une permutation de 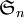
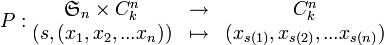
(où
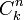 désigne
désigne 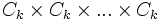 )
)- Les rotations d'un quart de tour dans le sens direct sont appelées
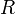 ,
, 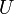 ,
, 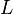 ,
,  ,
, 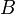 ,
,  pour les faces
pour les faces
droite (right), haut (up), gauche (left), avant (front), arrière (back) et bas (down).
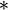 l'opérateur de composition (avec
l'opérateur de composition (avec ![(f*g)(x) = g[f(x)] \,](/pictures/frwiki/55/753e80a958f6378a519ffe022e656e38.png) ).
).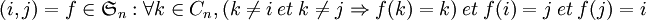
Décomposition des mouvements du cube
Isomorphisme
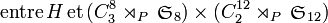
Permutation des arêtes et des sommets
On associe au Rubik's cube une numérotation des faces et une autre pour les sommets.
On définit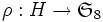 la permutation concernant les sommets et
la permutation concernant les sommets et 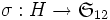 celle des arêtes.
celle des arêtes.
On a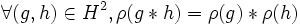 et de même
et de même 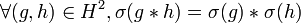 .
.
En utilisant la notation des cycles, on a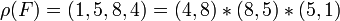 et
et 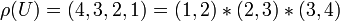 , d'où
, d'où 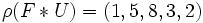 . (attention : la notation des cycles est davantage adaptée à la loi
. (attention : la notation des cycles est davantage adaptée à la loi  : si
: si 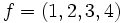 , on a
, on a 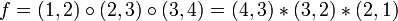 et
et 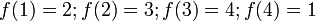 )
)Orientation des arêtes et des sommets
Pour chacun des sommets du cube, on place un marqueur noté
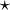 qui permet de déterminer son orientation .
qui permet de déterminer son orientation .- Emplacement des marqueurs :
Pour les sommets :
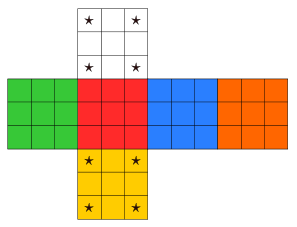
Pour les arêtes :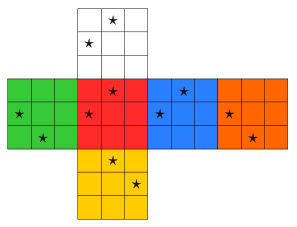
L'orientation sera alors le nombre de rotations de 120° à effectuer sur le cube pour rétablir la place du marqueur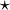 et on définit
et on définit 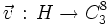 tel que
tel que 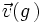 soit la réorientation des coins associée au mouvement
soit la réorientation des coins associée au mouvement 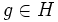 .
.
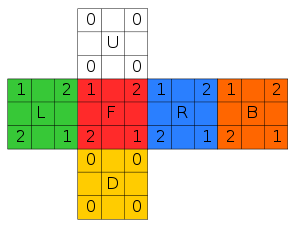
On définit de même l'orientation des arêtes par le nombre de rotations de 180° permettant de rétablir l'orientation initiale :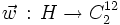 . On a :
. On a : 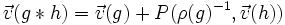
et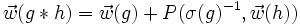
Exemple :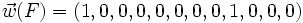 ,
, 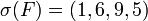 ,
, 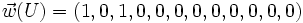 et
et 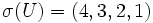
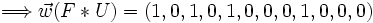 et
et 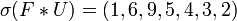
L'isomorphisme
Soit
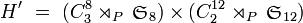 , on définit l'opération
, on définit l'opération 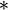 par :
par :
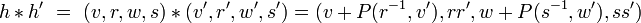 .
.
L'application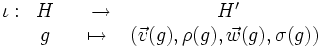 est un isomorphisme.
est un isomorphisme.
En effet, étant donné que
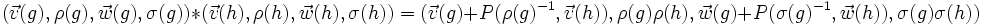 ,
,
l'application ι est un morphisme.
De plus, elle est injective car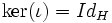 (en effet si aucun cube n'est déplacé ou réorienté, c'est que le cube est resté invariant !).
(en effet si aucun cube n'est déplacé ou réorienté, c'est que le cube est resté invariant !).
Elle est nécessairement surjective car en démontant le cube (on est ici dans le groupe élargi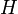 ), on peut parvenir à n'importe quelle configuration du Rubik's Cube.
), on peut parvenir à n'importe quelle configuration du Rubik's Cube.Théorème fondamental : caractérisation des mouvements légaux
Soit
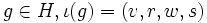 .
.
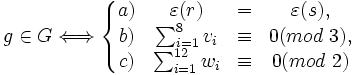 .
.Démonstration de la partie directe
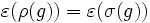
Soit
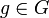 .
.On a
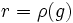 et
et 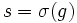 . On écrit
. On écrit 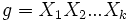 , où
, où 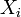 est un mouvement parmi
est un mouvement parmi 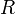 ,
, 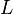 ,
, 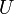 ,
,  ,
, 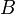 et
et 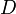 .On démontre que pour chacun de ces mouvements, que
.On démontre que pour chacun de ces mouvements, que 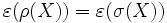 . Étant donné que
. Étant donné que  ,
, 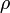 ,
, 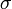 sont des morphismes, on a alors :
sont des morphismes, on a alors :
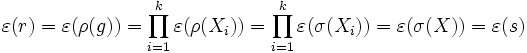 .
.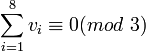
Vérifions que cette relation est valable pour les six rotations "de base" :
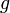
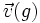

(2,0,0,1,1,0,0,2) 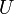
(0,0,0,0,0,0,0,0) 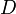
(0,0,0,0,0,0,0,0) 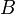
(0,1,2,0,0,2,1,0) 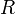
(1,2,0,0,2,1,0,0) 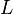
(0,0,1,2,0,0,2,1) Il est immédiat que
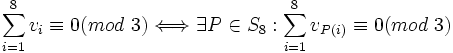 et que si deux familles
et que si deux familles 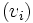 et
et 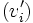 vérifient b), alors la famille
vérifient b), alors la famille 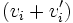 vérifie b) également.
vérifie b) également.On écrit le mouvement g de la même manière que précédemment (
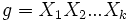 ), on suppose de plus qu'il s'agit d'une expression minimale du mouvement (ie on ne peut l'écrire avec moins de mouvements). L'entier k est appelé longueur de g (il s'agit de la distance entre g et l'identité dans le graphe de Cayley de G.)
), on suppose de plus qu'il s'agit d'une expression minimale du mouvement (ie on ne peut l'écrire avec moins de mouvements). L'entier k est appelé longueur de g (il s'agit de la distance entre g et l'identité dans le graphe de Cayley de G.)On peut donc prouver b) par induction sur la longueur du mouvement. La longueur k=1 a déjà été vérifiée (si k = 1, alors
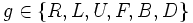 ).
).Supposons k>1. On a
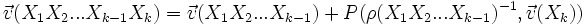 .
. 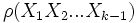 étant une permutation de
étant une permutation de 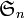 ,
, 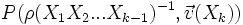 vérifie b), de plus d'après l'hypothèse d'induction,
vérifie b), de plus d'après l'hypothèse d'induction, 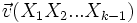 le vérifie également. Comme leur somme le vérifie, on obtient la relation.
le vérifie également. Comme leur somme le vérifie, on obtient la relation.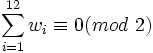
Idem que précédemment en remplaçant ρ par σ
Démonstration de la réciproque
Soit
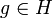 vérifiant les trois points présentés précédemment.
vérifiant les trois points présentés précédemment.On démontre d'abord la réciproque dans des cas particuliers, pour arriver ensuite au cas général.
v quelconque,
![r=id_{[[1,8]]} ; s=id_{[[1;12]]} ; (w_i)_{1\le i \le 12}=(0,0...,0)](/pictures/frwiki/52/481725d16f678f391c4d9893bb7f476b.png)
Il existe un mouvement qui tourne deux coins (sans les permuter) et qui préserve l'orientation et la position de chacun des autres cubes. En modifiant ce mouvement, on peut générer l'ensemble des 8-uplets vérifiant b) Certains de ces mouvements seront ajoutés par la suite
w quelconque,
![r=id_{[[1,8]]} ; s=id_{[[1;12]]} ; (v_i)_{1\le i \le 8}=(0,0...,0)](/pictures/frwiki/49/1309a0b1f93502e83f6058e2be45a049.png)
Il est possible de retourner deux arêtes et de laisser le reste invariant. On génère alors l'ensemble des 12-uplets vérifiant c).
v et w quelconques,
![r=id_{[[1,8]]} ; s=id_{[[1;12]]} \,](/pictures/frwiki/102/f80633dd65d76f4a6e04e09222b25d47.png)
Soit
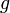 défini par
défini par ![(v,id_{[[1,8]]},w,id_{[[1,12]]}) \,](/pictures/frwiki/49/19162d8e37bf2dc7bd3c2bde99c37ff3.png) ,
, 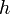 et
et 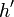 définis par
définis par ![(v,id_{[[1,8]]},0,id_{[[1,12]]}) \,](/pictures/frwiki/99/ce4ca9e4c1e94b0f0ea7fb1d080fb648.png) et
et ![(0,id_{[[1,8]]},w,id_{[[1,12]]}) \,](/pictures/frwiki/57/952f85b8d1e36ee87c042acdd487274e.png) .
.
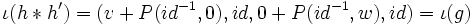 , alors comme
, alors comme  est bijective, on en déduit
est bijective, on en déduit 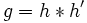 : c'est la composée de deux mouvements "légaux", donc
: c'est la composée de deux mouvements "légaux", donc 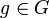 .
.r et s quelconques,
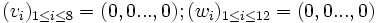
On montre en utilisant la relation a) que ce mouvement appartient à

(A approfondir)
v,r,w,s quelconques
Soit
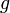 vérifiant a) b) et c). Alors
vérifiant a) b) et c). Alors 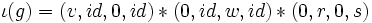 et chacun de ces trois mouvements est légal, donc
et chacun de ces trois mouvements est légal, donc 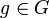 .
.Calcul du cardinal du groupe des mouvements du Rubik's Cube
- On élargit le groupe en supprimant la condition a) par
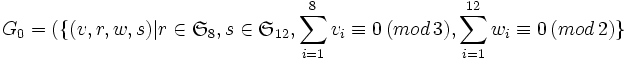 .
.
On définit sur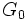 l'opération
l'opération 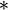 par
par 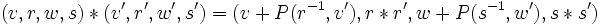 .
.
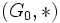 est un groupe :
est un groupe :-
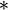 est interne
est interne- l'associativité de
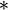 :
:
- est évidente pour
 et
et 
- découle (pour
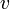 et
et 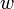 ) du fait que
) du fait que 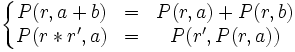 (attention à l'opération
(attention à l'opération 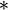 )
)
- est évidente pour
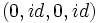 est élément neutre
est élément neutre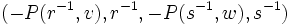 est l'inverse de
est l'inverse de 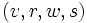
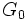 est isomorphe à
est isomorphe à 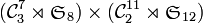
avec
![\mathcal{C}_n^k=\{(v_1,v_2,...,v_k,v_{k+1} | \forall i \in [[1,k+1]], v_i \in [[0,n-1]] \, \mbox{et} \, \sum_{i=1}^{k+1} v_i \equiv 0 \,(mod \, n) \}](/pictures/frwiki/102/fbe98fac132d26a08af8a841d1b20fa1.png) ,
,
ie![\mathcal{C}_n^k=\{(v_1,v_2,...,v_k,\overline{ \left(-\sum_{i=1}^{k} v_i \right) } \, | \, \forall i \in [[1,k]], v_i \in [[0,n-1]] \}](/pictures/frwiki/101/e1c221ee60c2821aa9182ddd4e1f506f.png) , où
, où 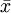 désigne la classe d'équivalence de x dans
désigne la classe d'équivalence de x dans 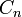 .
.
On obtient ainsi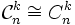 ,
,
et on en déduit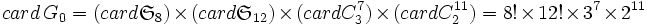
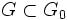 et
et 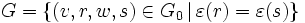
Soit
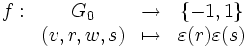 , on a
, on a 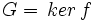 .
.- Montrons que
 est un sous-groupe normal de
est un sous-groupe normal de 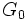 .
.
- D'après la caractérisation des sous-groupes,
 est un sous-groupe de
est un sous-groupe de 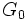 .
. 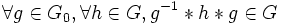 .
.
- on a
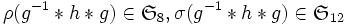 .
. - comme
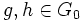 , alors les propriétés b) et c) sont vérifiées par
, alors les propriétés b) et c) sont vérifiées par 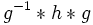 (structure de groupe).
(structure de groupe). 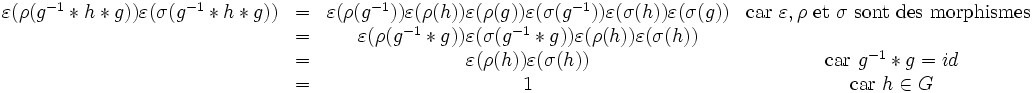
- on a
- D'après la caractérisation des sous-groupes,
Donc
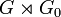 , et le groupe quotient
, et le groupe quotient 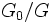 existe.
existe.- Calcul de l'indice de
 dans
dans 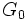 :
:
Soit
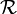 la relation définie par
la relation définie par 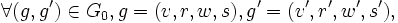
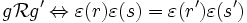
Soit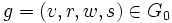 et
et 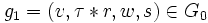 où
où 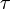 est une transposition.
est une transposition.
Soit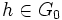 , on a
, on a 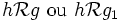 , d'où
, d'où 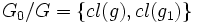 .
.
On en déduit que l'indice de dans
dans 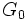 est
est ![[G_0:G] =|G_0/G|=2 \,](/pictures/frwiki/48/0cf84ddd1cb214a86c2aeaef6154c6fc.png) .
.
D'après le théorème de Lagrange,![|G|=|G_0| / [G_0:G] = \underline{8!12!2^{10}3^7} \,](/pictures/frwiki/50/275bf2c3edf7c8a7d8d7f847db7cc740.png)
Générateurs et relations
Bibliographie
- [pdf] Mathematics of the Rubik's Cube, W.D. Joyner
- Portail des mathématiques
- Portail des jeux
Catégories : Algorithme | Rubik's Cube | Théorie des groupes
Wikimedia Foundation. 2010.
