- Théorie d'Everett
-
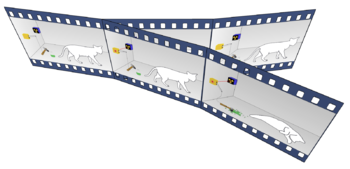Le paradoxe du chat de Schrödinger dans l'interprétation d'Everett des mondes multiples (many worlds). Ici, chaque événement est une bifurcation. Le chat est à la fois mort et vivant, avant même l'ouverture de la boîte, mais le chat mort et le chat vivant existent dans des bifurcations différentes de l'univers, qui sont tout aussi réelles l'une que l'autre.
La théorie d'Everett, appelée aussi théorie des états relatifs, ou encore théorie des mondes multiples, est une interprétation de la mécanique quantique visant à résoudre le problème de la mesure quantique.
Sommaire
Contexte
Hugh Everett, qui l'a développée, estimait invraisemblable qu'une fonction d'onde déterministe donne lieu à des observations qui ne le sont pas, conséquence pourtant d'un postulat de la mécanique quantique, celui de la réduction du paquet d'onde. Ce postulat pose également un problème de cohérence mathématique avec le problème de la mesure quantique dans cette même théorie.
Selon lui, la seule source d'anti-hasard possible était l'observateur lui-même, ou plus exactement : sa nature d'observateur qui lui était propre (le résultat qu'il observait le caractérisant lui-même en tant que cet observateur) et ne concernait pas l'univers qui restait parfaitement neutre et comportait toutes les possibilités prévues par la théorie quantique. Les possibilités par lui observées définissaient seules l'observateur, qui ne percevait donc que cet univers-là[1]
Cette interprétation inhabituelle rappelant le principe de l'action et de la réaction fut exposée dans sa thèse de doctorat en 1957 sous la direction de John Wheeler (voir la biographie). Celui-ci, réticent au départ, devint par la suite partisan enthousiaste de cette théorie - certes la seule à rendre compte sans paradoxe de la mécanique quantique - et nombre de physiciens au nombre desquels David Deutsch et Colin Bruce la considèrent la seule possible à ne pas nécessiter quelque deus ex machina introduisant en permanence de l'anti-hasard dans l'univers. Sans indiquer réellement son opinion sur cette théorie, Murray Gell-Mann montre pour elle, dans son livre le Quark et le Jaguar, une sympathie bienveillante.
On peut rapprocher cette théorie des calculs fondés sur l'ensemble des possibilités offertes au système, tels que l'intégrale de Feynman ou intégrale de chemin de Richard Feynman, ou le Principe des puissances virtuelles.
La principale interprétation concurrente est l'interprétation transactionnelle de la mécanique quantique, plus étrange encore puisqu'elle fait l'hypothèse de messages allant dans les deux sens du temps.
Humour éverettien
Le côté paradoxal du monde d'Everett a fait naître chez les physiciens de nombreuses plaisanteries estudiantines, comme par exemple la suivante :
« Deux physiciens prennent un avion. En route, les deux moteurs s'arrêtent et l'avion pique vers le sol. "Crois-tu que nous allons nous en sortir ?", demande le premier. "Sans aucun problème", répond l'autre "il y a une quantité d'univers où nous ne sommes même pas montés dans cet avion" ».
Citation de David Deutsch
« We know that no single-universe theory can explain even the Einstein–Podolsky–Rosen experiment », Many Worlds? Everett, Quantum Theory, and Reality, 2010, ISBN 978-0-19-956056-1, page 542.
Nous savons qu'aucune théorie à un seul univers ne permet d'expliquer ne serait-ce que l'expérience EPR (de 1982, voir Alain Aspect).Voir aussi
- Hugh Everett
- Multivers
- Effet Glapion
- Théorème de Gleason
- David Deutsch
Notes et références
- « Everett questions what happens to the observer of a quantum mechanical measurement: ‘Why doesn’t our observer see a smeared out needle? The answer is quite simple. He behaves just like the apparatus did. When he looks at the needle (interacts) he himself becomes smeared out, but at the same time correlated to the apparatus, and hence to the system (...) the observer himself has split into a number of observers, each of which sees a definite result of the measurement. As an analogy one can imagine an intelligent amoeba with a good memory. As time progresses the amoeba is constantly splitting », Many Worlds? Everett, Quantum Theory, and Reality, Oxford University Press, ISBN 978-0-19-956056-1
Liens externes
- (en) Many-Worlds Interpretation of Quantum Mechanics, une compilation d'articles réalisée par Norman Hugh Redington sur son site The Net Advance of Physics
- (en) Distinction entre "Many-worlds" et "Many-minds" [PDF]
- (en) The Everett FAQ
Catégorie :- Interprétation de la mécanique quantique
Wikimedia Foundation. 2010.
