Theoreme des livres ouverts

Theoreme des livres ouverts

Théorème des livres ouverts

Le théorème des livres ouverts de Giroux est un pont entre la géométrie de contact et la topologie différentielle. Il fait le lien entre les structures de contact et les décompositions en livre ouvert qui, en dimension trois, sont des objets purement topologiques. En dimension trois le théorème a une démonstration purement topologique et a eu de nombreuses conséquences en topologie en basse dimension. En grandes dimensions la preuve est analytique et les conséquences sont moins nombreuses, sans doute principalement à cause du peu de connaissances disponible sur les groupes de symplectomorphismes.

Sommaire

Définitions

Dans toute la suite, V désigne un variété différentielle de dimension impaire 2n + 1 close et orientée. Un livre ouvert de V est un couple (K,θ) où

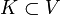  • K \subset V est une sous-variété close de codimension deux à fibré normal trivial ;
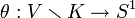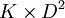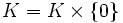  • \theta : V \smallsetminus K \to S^1 est une fibration qui, dans un voisinage K \times D^2 de K = K \times \{ 0 \}, coïncide avec la coordonnée angulaire sur le disque D2.

La sous-variété K est appelée reliure du livre ouvert et l'adhérence d'une fibre de θ est appelée page du livre ouvert. L'orientation de S1 fourni une coorientation des fibres (et donc des pages) qui est convertie en orientation par l'orientation de V. Cette orientation fourni à son tour une orientation de la reliure comme bord des pages.

Le lien avec les structures de contact est fourni par la définition suivante due à Giroux où les orientation définies plus haut servent de référence :

Une structure de contact est portée par le livre ouvert (K,θ) si elle peut être définie par une forme de contact α telle que :

  • α induit sur K une forme de contact positive ;
  • dα induit sur chaque fibre F de θ une forme symplectique positive.

Une telle forme α sera dite adaptée à (K,θ). En dimension trois, on peut exprimer cette relation en termes de champ de Reeb : la forme α est adaptée à (K,θ) si et seulement si son champ de Reeb R est positivement tangent à la reliure et positivement transverse aux fibres.

Pour établir un lien bijectif avec les structures de contact à isotopie près on doit introduire la notion de stabilisation dont on donne ici la définition en dimension trois seuleument : Soit F une surface compacte à bord plongée dans V et a un arc simple et propre de F. On dit qu'une surface compacte F' est obtenue à partir de F par le plombage positif d'un anneau le long de a si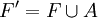 F' = F \cup A où A est un anneau plongé dans V tel que :

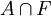  • A \cap F est un voisinage régulier de a dans F;
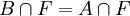
  • A est inclus dans une boule fermée B vérifiant B\cap F =A \cap F

et l'enlacement des deux composantes de bord de A dans B vaut 1. D'après un théorème de Stallings, si F est une page d'un livre ouvert (K,θ) et si F' est obtenue à partir de F par plombage d'un anneau, alors il existe un livre ouvert de V dont F' est une page. On appelle stabilisation une suite finie de plombages positifs.

Exemples

Dans 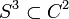S^3\subset C^2 muni des coordonnées polaires 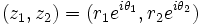(z_1,z_2)=(r_1e^{i\theta_1},r_2e^{i\theta_2}) le nœud trivial {r1 = 0} est la reliure du livre ouvert dont la fibration est simplement θ1 et dont les pages sont de disques. En projection stéréographique dans 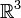\R^3 dont le pôle est sur la reliure, le livre ouvert devient le couple (Oz,θ) en coordonnées cylindriques (z,r,θ). On voit donc les pages d'un livre dont la reliure est infinie et qu'on a ouvert à 360°.

On peut appliquer à ce livre ouvert l'opération de plombage (positif ou négatif) et obtenir comme reliure l'entrelac de Hopf positif ou négatif qui sont définis comme

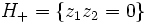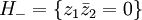
H_+=\{z_1z_2=0\}~ et H_-=\{z_1\bar z_2=0\}

avec comme fibration 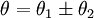\theta=\theta_1\pm\theta_2. Les pages de ces deux livres ouverts sont des anneaux.

Les deux premiers exemples portent la structure de contact canonique sur la sphère (voir les exemples de géométrie de contact) mais celui dont la reliure est H − porte une structure de contact vrillée.

Les énoncés

La définition de structure de contact portée par un livre ouvert permet de réinterpréter le théorème de Thurston-Winkelnkemper ainsi :

Théorème de Thurston-Winkelnkemper — Tout livre ouvert porte au moins une structure de contact.

Et maintenant le théorème de Giroux :

Théorème de Giroux — Soit V une variété close de dimension trois.

  • Toutes les structures de contact portées par un même livre ouvert de V sont isotopes.
  • Toute structure de contact de V est portée par un livre ouvert.
  • Deux livres ouverts de V portant des structures de contact isotopes ont des stabilisations isotopes.

On peut donc résumer la situation ainsi : la notion de structure de contact portée par un livre ouvert établit une bijection entre les structures de contact à isotopie près et les livres ouverts à isotopie et stabilisation près.

En grandes dimensions

En dimension plus grandes que 5, il existe aussi des théorèmes analogues dus à Giroux et Mohsen mais qui demandent un peu plus de définitions.

Références

  • Giroux, E. Géométrie de contact : de la dimension trois vers les dimensions supérieures, Proceedings of the ICM, Beijing 2002, vol. 2, 405-414
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Th%C3%A9or%C3%A8me des livres ouverts ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme des livres ouverts de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

  • Théorème des livres ouverts — Le théorème des livres ouverts de Giroux est un pont entre la géométrie de contact et la topologie différentielle. Il fait le lien entre les structures de contact et les décompositions en livre ouvert qui, en dimension trois, sont des objets… …   Wikipédia en Français

  • Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants  …   Wikipédia en Français

  • Theoreme de Cauchy-Lipschitz — Théorème de Cauchy Lipschitz Pour les articles homonymes, voir Cauchy. Cauchy développe une première version du théorème de l article. Le …   Wikipédia en Français

  • Théorème de Picard-Lindelöf — Théorème de Cauchy Lipschitz Pour les articles homonymes, voir Cauchy. Cauchy développe une première version du théorème de l article. Le …   Wikipédia en Français

  • Théorème de cauchy-lipschitz — Pour les articles homonymes, voir Cauchy. Cauchy développe une première version du théorème de l article. Le …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

  • Théorème de Cauchy-Lipschitz — Pour les articles homonymes, voir Cauchy. Cauchy développe une première version du théorème de l article. En mathématiques, et plus précisément en a …   Wikipédia en Français

  • Corps des réels — Nombre réel Les nombres réels (dont l ensemble est noté ℝ) peuvent très informellement être conçus en mathématiques comme tous les nombres associés à des longueurs ou des grandeurs physiques. Ce sont les nombres, qu ils soient positifs, négatifs… …   Wikipédia en Français

  • Forme de contact — Géométrie de contact Structure standard sur ℝ3 : champ de plans La géométrie de contact est la partie de la géométrie différentielle qui étudie les formes et structures de contact. Elle entretient d étroits liens avec la géométrie… …   Wikipédia en Français

  • Geometrie de contact — Géométrie de contact Structure standard sur ℝ3 : champ de plans La géométrie de contact est la partie de la géométrie différentielle qui étudie les formes et structures de contact. Elle entretient d étroits liens avec la géométrie… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”