Tableaux de Young

Les tableaux de Young sont des objets combinatoires qui jouent un rôle important en théorie des représentations des groupes et dans la théorie des fonctions symétriques. Ils permettent en particulier de construire les représentations irréductibles du groupe symétrique, ainsi que celles du groupe général linéaire sur le corps des complexes.

Sommaire 1 Définition 1.1 Diagramme de Young 1.2 Tableau de Young 2 Monoïde plaxique 2.1 Algorithme de Schensted 2.2 Relations de Knuth 3 Applications 3.1 Représentations du groupe symétrique 3.2 Représentation de GL(E) 3.3 Fonctions symétriques

Définition

Diagramme de Young

Un diagramme de Young, ou diagramme de Ferrer, est en quelque sorte une représentation graphique d'une partition d'un entier. Il est constitué d'un ensemble de cases justifiées à gauche et en bas, et le nombre de cases de chaque ligne correspond aux éléments de la partition associée. L'image à droite montre le diagramme associé à la partition (3,3,1).

Tableau de Young

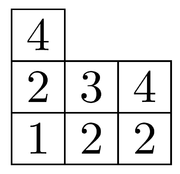
Un tableau de Young à valeurs dans [m] est un diagramme de Young dont les cases sont remplies par des entiers compris entre 1 et m, avec la contrainte que les lignes doivent être croissantes au sens large, et les colonnes croissantes au sens stricte. La partition associée au diagramme sous-jacent s'appelle la forme du tableau.

Monoïde plaxique

Algorithme de Schensted

L'algorithme de Schensted permet d'insérer une suite d'entiers dans un tableau, de manière à obtenir un nouveau tableau. Cet algorithme permet :

• de munir l'ensemble des tableaux d'une loi de composition interne, en insérant successivement les éléments d'un tableau dans un autre.
• d'induire une relation d'équivalence sur l'ensemble des suites finies d'entiers (cad des mots sur l'alphabet [m]). En effet, étant donnée une telle suite, il est possible de l'insérer dans le tableau vide : on obtient un tableau qui s'appelle le P-symbole de la suite. Deux suites seront équivalentes si elles sont le même P-symbole.

Relations de Knuth

À partir de l'étude de cette relation d'équivalence sur les mots de longueur 3, Donald Knuth a défini des règles de réécriture sur l'ensemble des mots sur [m]. Ces règles de réécriture induisent également une relation d'équivalence, et Knuth a démontré qu'elle coïncide avec la relation de Schensted. Une conséquence importante de ce théorème est que la loi de composition qui découle de l'algorithme de Schensted possède toutes les propriétés requises pour donner à l'ensemble des tableaux une structure de monoïde : le monoïde plaxique.

Applications

Représentations du groupe symétrique

Les tableaux de Young permettent de calculer simplement les symétriseurs de Young.

Représentation de GL(E)

Si E est un -espace vectoriel de dimension m, et λ une partition, on définit le module de Schur E^λ comme étant le -espace vectoriel dont une base est formée par l'ensemble des tableaux de Young de forme λ et à valeur dans [m]. Sachant qu'il est possible d'identifier un tableau de Young à valeurs dans [m] à un polynôme de , il existe une action naturelle de GL(E) sur les tableaux de Young par simple multiplication matricielle. Les modules de Schur sont donc des représentations de GL(E). On peut montrer que toute représentation polynomiale irréductible de GL(E) est isomorphe à un unique module de Schur.

Fonctions symétriques

Les caractères des modules de Schur (en tant que représentations de GL(E)) sont des polynômes symétriques appelés polynômes de Schur. Les tableaux de Young fournissent un moyen élégant pour exprimer ces polynômes. Par ailleurs, il existe une règle purement combinatoire qui fait appel aux tableaux de Young, et qui permet de décomposer le produit de deux polynômes de Schur. Ceci implique en particulier que les tableaux permettent de décomposer le produit tensoriel de deux représentations irréductibles de GL(E) en somme directe de représentation irréductibles.

• Portail des mathématiques