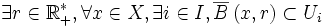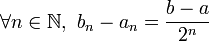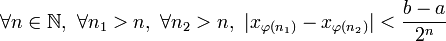TBW

TBW

Théorème de Bolzano-Weierstrass

En topologie des espaces métriques, le théorème de Bolzano-Weierstrass donne une caractérisation séquentielle des espaces compacts. Il tire son nom des mathématiciens Bernard Bolzano et Karl Weierstrass.

Sommaire

Énoncé du théorème

Un espace métrique (X,d) est compact (au sens de l'axiome de Borel-Lebesgue) si et seulement si toute suite à valeurs dans X admet une valeur d'adhérence dans X.

Démonstration

Sens direct

On suppose que de tout recouvrement ouvert on peut extraire un sous-recouvrement fini.

Soit 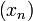\left(x_{n}\right) une suite d'éléments de X. Montrons que 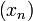\left(x_{n}\right) admet une valeur d'adhérence.

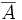Notons F_{n}=\overline{\left\{ x_{k},k\in\left[n,+\infty\right[\right\} } (où \overline{A} désigne l'adhérence de A).

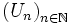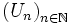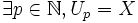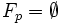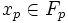Posons alors U_{n}=X\setminus F_{n}. Si la famille \left(U_{n}\right)_{n\in\mathbb{N}} était un recouvrement de X alors par hypothèse on pourrait en extraire un sous recouvrement fini; or \left(U_{n}\right)_{n\in\mathbb{N}} est une famille croissante d'ensembles donc \exists p\in\mathbb{N},U_{p}=X mais alors F_{p}=\emptyset ce qui est exclu car x_{p}\in F_{p}.

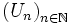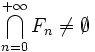
\left(U_{n}\right)_{n\in\mathbb{N}} n'est donc pas un recouvrement donc \bigcup_{n=0}^{+\infty}U_{n}\neq X, donc \bigcap_{n=0}^{+\infty}F_{n}\neq\emptyset

Ce qui montre par définition que 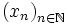\left(x_{n}\right)_{n\in\mathbb{N}} admet une valeur d'adhérence.

Sens réciproque

Dans cette démonstration, on qualifiera de séquentiellement compact un espace métrique dans lequel toute suite admet une valeur d'adhérence.

Premier lemme (nombres de Lebesgue d'un recouvrement)

Si 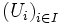\left(U_{i}\right)_{i\in I} est un recouvrement ouvert d'un espace séquentiellement compact X, alors

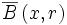\exists r\in\mathbb{R}_{+}^{*},\forall x\in X,\exists i\in I,\overline{B}\left(x,r\right)\subset U_{i}

(Où \overline{B}\left(x,r\right) désigne la boule fermée de centre x et de rayon r.)


Démonstration

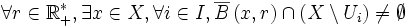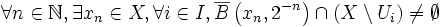Par l'absurde. on suppose \forall r\in\mathbb{R}_{+}^{*},\exists x\in X,\forall i\in I,\overline{B}\left(x,r\right)\cap(X\setminus U_{i})\neq\emptyset en particulier \forall n\in\mathbb{N},\exists x_{n}\in X,\forall i\in I,\overline{B}\left(x_{n},2^{-n}\right)\cap(X\setminus U_{i})\neq\emptyset .

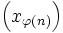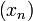X est séquentiellement compact donc il existe une suite extraite \left(x_{\varphi\left(n\right)}\right) de \left(x_{n}\right) convergeant vers x\in X.

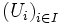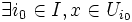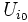Comme \left(U_{i}\right)_{i\in I} est un recouvrement de X on a \exists i_{0}\in I,x\in U_{i_{0}} or U_{i_{0}} est un ouvert donc 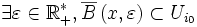\exists\varepsilon\in\mathbb{R}_{+}^{*},\overline{B}\left(x,\varepsilon\right)\subset U_{i_{0}} or on peut choisir 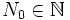N_{0}\in\mathbb{N} tel que 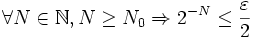\forall N\in\mathbb{N},N\geq N_{0}\Rightarrow2^{-N}\leq\frac{\varepsilon}{2}, comme 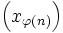\left(x_{\varphi\left(n\right)}\right) converge vers x il existe 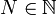N\in\mathbb{N} tel que 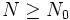N\geq N_{0} et 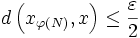d\left(x_{\varphi\left(N\right)},x\right)\leq\frac{\varepsilon}{2}.

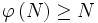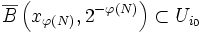Comme \varphi\left(N\right)\geq N on a \overline{B}\left(x_{\varphi\left(N\right)},2^{-\varphi\left(N\right)}\right)\subset U_{i_{0}} ce qui est absurde.

Deuxième lemme (précompacité)

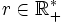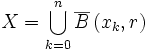Si X est un espace métrique séquentiellement compact, alors pour tout nombre r\in\mathbb{R}_{+}^{*} il existe une suite finie de points \displaystyle \left(x_{k}\right)_{k\in\left[\left[0,n\right]\right]} de X tel que:X=\bigcup_{k=0}^{n}\overline{B}\left(x_{k},r\right)


Démonstration

Par l'absurde. On nie le résultat, puis on construit une suite qui nous permettra de trouver une contradiction.

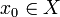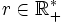Soit x_{0}\in X et r\in\mathbb{R}_{+}^{*}. On suppose construit les termes \displaystyle x_{0},x_{1}...x_{n} de la suite jusqu'au rang 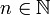n\in\mathbb{N} tel que \forall\left(i,j\right)\in\left[\left[0,n\right]\right]^{2},i\neq j\Rightarrow d\left(x_{i},x_{j}\right)\geq r. Par hypothèse on peut choisir 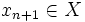x_{n+1}\in X tel que x_{n+1}\notin\bigcup_{k=0}^{n}\overline{B}\left(x_{k},r\right).

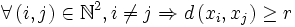On peut donc construire par récurrence une suite \left(x_{k}\right)_{k\in\mathbb{N}} tel que \forall\left(i,j\right)\in\mathbb{N}^{2},i\neq j\Rightarrow d\left(x_{i},x_{j}\right)\geq r donc \left(x_{k}\right)_{k\in\mathbb{N}} n'admet pas de sous-suite convergente ce qui est en contradiction avec l'hypothèse X est un espace métrique séquentiellement compact.

Fin de la démonstration du théorème

Supposons X séquentiellement compact. Soit 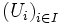\left(U_{i}\right)_{i\in I} un sous recouvrement ouvert de X.

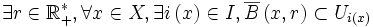D'après le premier lemme: \exists r\in\mathbb{R}_{+}^{*},\forall x\in X,\exists i\left(x\right)\in I,\overline{B}\left(x,r\right)\subset U_{i\left(x\right)}.

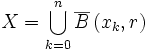D'après le lemme de précompacité, pour ce r donné il existe une suite finie de points \left(x_{k}\right)_{k\in\left[\left[0,n\right]\right]} de X tel que X=\bigcup_{k=0}^{n}\overline{B}\left(x_{k},r\right).

On en déduit donc que la sous-famille \left(U_{i\left(x_{k}\right)}\right)_{k\in\left[\left[0,n\right]\right]} recouvre X.

Énoncé dans le cas réel

De toute suite réelle bornée, on peut extraire une sous-suite convergente.

Pour montrer cette propriété, il suffit de remarquer que les intervalles fermés bornés de \R sont compacts (théorème de Borel-Lebesgue). La même propriété s'applique aux suites bornées complexes, ou plus généralement aux suites bornées de vecteurs dans un espace vectoriel normé de dimension finie.


Démonstration élémentaire

Soit 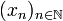(x_n)_{n \in \N} une suite à valeurs dans un segment [a,b] de \R. La démonstration procède en deux temps :

1) Construction de deux suites 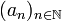(a_n)_{n\in \mathbb{N}} (resp. 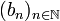(b_n)_{n\in \mathbb{N}}) croissante (resp. décroissante) telles que l'intervalle [a,b] contient une infinité de termes de la suite 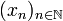(x_n)_{n\in \mathbb{N}} et que
\forall n\in\mathbb{N},\ b_n-a_n= \frac{b-a}{2^n}
2) Construction de la suite extraite.
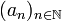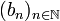1) Construction par dichotomie des suites (a_n)_{n\in \mathbb{N}} (resp. (b_n)_{n\in \mathbb{N}} )

On définit a0 par a0 = a et b0 par b0 = b.

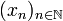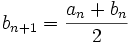Pour tout entier naturel n, si l'intervalle \left[ a_n , \frac{a_n+b_n}{2} \right] contient une infinité de termes de la suite (x_n)_{n\in \mathbb{N}}, on pose an + 1 = an et b_{n+1} = \frac{a_n+b_n}{2}.

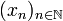Sinon, l'intervalle \left[ \frac{a_n+b_n}{2},b_n \right] contient une infinité de termes de la suite (x_n)_{n\in \mathbb{N}}, on pose alors 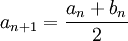a_{n+1} = \frac{a_n+b_n}{2} et bn + 1 = bn.

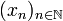On vérifie que ces deux suites ainsi construite sont adjacentes et que l'intervalle [a,b] contient une infinité de termes de la suite (x_n)_{n\in \mathbb{N}} .

2) Construction par récurrence de la suite extraite convergente

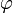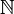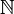Cela revient à dire que nous cherchons une fonction \varphi de \mathbb{N} dans \mathbb{N} strictement croissante, telle que la suite 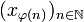(x_{\varphi (n)})_{n\in \mathbb{N}} soit convergente. Construisons alors la fonction 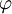\varphi\; par récurrence.

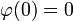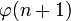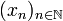Posons \varphi(0)=0. Pour tout entier n, prenons pour \varphi(n+1) le plus petit entier m strictement supérieur à \varphi(n) tel que x_m\in \left[ a_{n+1},b_{n+1} \right] (cet entier existe puisque \left[ a_{n+1}\ ,b_{n+1}\ \right] contient une infinité de termes de la suite (x_n)_{n\in \mathbb{N}} ). La fonction 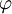\varphi\; est donc bien définie par récurrence et par construction cette fonction est strictement croissante et vérifie la propriété:

\forall n\in\mathbb{N},\ \forall n_1>n,\ \forall n_2>n,\ |x_{\varphi(n_1)}-x_{\varphi(n_2)}|<\frac{b-a}{2^n}\;

Cette propriété nous montre que la suite 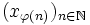(x_{\varphi (n)})_{n\in \mathbb{N}} \; vérifies le critère de Cauchy, elle est donc convergente vers un réel \ell appartenant à l'intervalle [a,b].

Voir aussi

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Th%C3%A9or%C3%A8me de Bolzano-Weierstrass ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article TBW de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • TBW — Abbreviation for total body water. * * * total body water; total body weight * * * total body water …   Medical dictionary

  • TBW — Total body weight (Medical » Physiology) * The Business Workshop (Business » General) * To Be Written (Community » Media) * T B Woods Corporation (Business » NYSE Symbols) * Threatened Birds of the World (Governmental » Environmental) * The… …   Abbreviations dictionary

  • TBW — Thermo Balanced Writing (Philips CD RW) …   Acronyms

  • tbw — ISO 639 3 Code of Language ISO 639 2/B Code : ISO 639 2/T Code : ISO 639 1 Code : Scope : Individual Language Type : Living Language Name : Tagbanwa …   Names of Languages ISO 639-3

  • TBW — Thermo Balanced Writing (Philips CD RW) …   Acronyms von A bis Z

  • TBW — abbr. Total Body Water …   Dictionary of abbreviations

  • TBW — • total body water; • total body weight …   Dictionary of medical acronyms & abbreviations

  • TBW — abbreviation to be withheld …   Useful english dictionary

  • total body water — (TBW) any of various estimates of the water content of the human body, taking into consideration the person s height, weight, and age; used in urea kinetic modeling calculations …   Medical dictionary

  • tə’xir — ə. TbW gecikdirmə, yubatma …   Klassik Azərbaycan ədəbiyyatında islənən ərəb və fars sözləri lüğəti

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”