- Série génératrice
-
Fonction génératrice
Sommaire
En mathématiques
En mathématiques, la fonction génératrice de la suite (an) est la série formelle définie par
On confond parfois la fonction génératrice et une fonction de la variable x. Cependant, il est utile de préciser qu'une fonction génératrice est avant tout une série formelle et que la fonction de la variable x correspondante risque de ne pas converger pour tout x.
- fonction génératrice de la suite constante 1 :
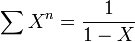
- fonction génératrice de la suite (n) :
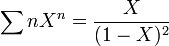
- fonction génératrice de la suite (n2) :
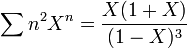
- fonction génératrice de la suite
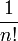 :
: 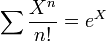
On parle aussi de fonction génératrice exponentielle de la suite (an) définie par la série formelle
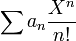 .
.Lorsque l'on travaille plutôt avec l'inverse de X, la variable z=1/X, on parle alors de la transformée en Z,
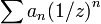 , qui est beaucoup utilisée en traitement du signal et en asservissements.
, qui est beaucoup utilisée en traitement du signal et en asservissements.On peut retrouver la suite initiale (an) à partir de la fonction génératrice F(X) (resp. la fonction génératrice exponentielle E(X)) selon les formules
En probabilité
Définition
Soit X une variable aléatoire entière et positive, la fonction génératrice de X est la série entière:
où P(X = k) est la probabilité que la variable aléatoire X prenne la valeur k.
Exemples pour les lois usuelles
- Pour la loi de Poisson de paramètre λ, on a
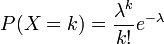 et il vient Gλ(t) = eλ(t − 1);
et il vient Gλ(t) = eλ(t − 1);
- Pour la loi binomiale de paramètres (n, p), on a
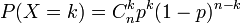 et on en déduit Gn,p(t) = (1 − p + pt)n.
et on en déduit Gn,p(t) = (1 − p + pt)n.
Propriétés
- Le rayon de convergence de cette série entière est toujours supérieur ou égal à 1.
- On peut remarquer que GX(t) = E[tX]
- Si X admet une espérance E[X] alors GX et sa dérivée sont définies en t=1 et on a:
- Si X admet une variance Var[X], et donc une espérance E[X], alors GX et ses dérivées première et seconde sont définies en t=1 et on a:
- Si deux variables aléatoires réelles discrètes à valeurs dans
 admettent la même fonction génératrice, alors elles ont la même loi de probabilité[1].
admettent la même fonction génératrice, alors elles ont la même loi de probabilité[1].
- Soient X et Y deux variables aléatoires réelles discrètes entières et positives. Si X et Y sont indépendantes alors on a:
-
- GX + Y = GX.GY
remarque:La réciproque est fausse.
Généralisation aux variables aléatoires non entières
Cette notion de fonction génératrice se généralise aux variables aléatoires continues par les fonctions caractéristiques. Une autre notion utile est la fonction génératrice des moments.
Voir aussi
Références
- ↑ Ce résultat est induit par le fait qu'il existe une relation bijective entre une loi de probabilité et sa fonction génératrice. La loi de probabilité définit la fonction génératrice F et, réciproquement, on retrouve la loi de probabilité à partir de F puisque pk = F(k)(0) / k!. Cette relation justifie l'appellation anglaise de Probability-generating function (en)
- Portail des mathématiques
- Portail des probabilités et des statistiques
Catégorie : Loi de probabilité
Wikimedia Foundation. 2010.

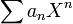
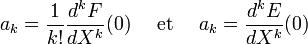
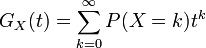
![E[X]= \frac{dG_X}{dt} (t=1)](/pictures/frwiki/57/9cba96d49c1b34c6b2659ea781f86110.png)
![Var[X]=\frac{d^2 G_X}{dt^2} (t=1) + \frac {dG_X} {dt} (t=1) - \left(\frac{dG_X}{dt} (t=1)\right)^2](/pictures/frwiki/101/e0ba8a85dfe22402d5992f9a987e0dc5.png)