- Symétrisable
-
Élément symétrique
En mathématiques, la notion d'élément symétrique généralise les concepts d'opposé en rapport avec l'addition, d'inverse en rapport avec la multiplication, d'application réciproque pour la composition d'applications. Intuitivement, un symétrique est un élément qui va défaire par composition, l'effet de la composition par un autre élément d'un élément donné.
Sommaire
Définition
Soit E un ensemble muni d'une loi de composition interne
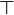 admettant un élément neutre
admettant un élément neutre 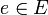 . Soit deux éléments a et b de E.
. Soit deux éléments a et b de E.- Si
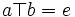 , a est dit élément symétrique à gauche (ou élément inverse à gauche) de b et b est dit élément symétrique à droite (ou élément inverse à droite) de a.
, a est dit élément symétrique à gauche (ou élément inverse à gauche) de b et b est dit élément symétrique à droite (ou élément inverse à droite) de a. - Si
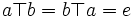 , a est dit 'élément symétrique (ou élément inverse) de b et réciproquement.
, a est dit 'élément symétrique (ou élément inverse) de b et réciproquement.
Un élément x de E qui admet au moins un symétrique à droite est dit symétrisable à droite (ou inversible à droite) ; s'il admet au moins un symétrique à gauche, il est dit symétrisable à gauche (ou inversible à gauche) ; s'il admet au moins un symétrique, il est dit symétrisable (ou inversible).
Propriétés
Dans le cas général, comme pour les éléments neutres à droite et à gauche, il est possible pour un élément donné y d'avoir plusieurs symétriques à droite, ou plusieurs symétriques à gauche. y peut même avoir plusieurs symétriques à droite et plusieurs symétriques à gauche.
Si la loi
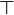 est associative, et si y possède à la fois un symétrique à droite et un symétrique à gauche, alors ils sont égaux et le symétrique est unique. Dans ce cas, l'ensemble des éléments symétrisables de E est un groupe appelé le groupe des unités de E et noté U(E) ou E * .
est associative, et si y possède à la fois un symétrique à droite et un symétrique à gauche, alors ils sont égaux et le symétrique est unique. Dans ce cas, l'ensemble des éléments symétrisables de E est un groupe appelé le groupe des unités de E et noté U(E) ou E * .Exemples
- Tout nombre réel x possède un symétrique du point de vue de l'addition, noté − x. Tout nombre réel non-nul possède un symétrique du point de vue de la multiplication, noté
 .
.
- Une matrice carrée M à coefficients dans un corps
 est inversible si et seulement si son déterminant est non nul. Si le déterminant de M est égal à zéro, elle ne possède aucun symétrique, à gauche comme à droite ; l'existence d'un symétrique à gauche ou à droite implique dans ce cas l'existence d'un symétrique.
est inversible si et seulement si son déterminant est non nul. Si le déterminant de M est égal à zéro, elle ne possède aucun symétrique, à gauche comme à droite ; l'existence d'un symétrique à gauche ou à droite implique dans ce cas l'existence d'un symétrique.
- De façon générale, une matrice carrée sur un anneau commutatif A est inversible si et seulement si son déterminant est inversible dans A.
- Une fonction g est l'inverse à gauche (respectivement à droite) d'une fonction f du point de vue de la composition de fonctions si et seulement si
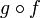 (respectivement
(respectivement 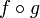 ) est l'application identité sur l'ensemble de définition (respectivement l'ensemble d'arrivée) de f.
) est l'application identité sur l'ensemble de définition (respectivement l'ensemble d'arrivée) de f.
Voir aussi
Catégorie : Algèbre générale - Si
Wikimedia Foundation. 2010.
