Symétrie de corinne

Symétrie de Corinne

Sommaire

1 Définition et exemple
2 Aspects historique
3 Utilisations
4 Notes et références de l'article
5 Voir aussi
- 5.1 Articles connexes

Définition et exemple

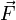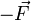En mécanique, changer le temps t réel en temps i.t imaginaire pur, revient à changer la force $\vec{F}$ en $-\vec{F}$ , dans la loi de Newton (principe fondamental de la dynamique)^[1] 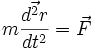$m\frac{\vec{d^{2}r}}{dt^{2}}=\vec{F}$ , passant ainsi par exemple d'une force attractive à une force répulsive et vice versa.

Démonstration: la transformation envisagée correspond au changement de variable t—> s=it dans la relation fondamentale de la dynamique. En utilisant la dérivée d'une fonction composée, il vient: 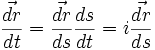$\frac{\vec{dr}}{dt}=\frac{\vec{dr}}{ds}\frac{ds}{dt}=i\frac{\vec{dr}}{ds}$ , par suite en répétant: 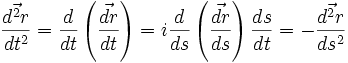$\frac{\vec{d^{2}r}}{dt^{2}}=\frac{d}{dt}\left (\frac{\vec{dr}}{dt}\right )=i\frac{d}{ds}\left (\frac{\vec{dr}}{ds}\right )\frac{ds}{dt}=-\frac{\vec{d^{2}r}}{ds^{2}}$ , d'où le résultat.

Aspects historique

Qui le premier a osé parler de temps imaginaire pur en gravité ?

Il existe des articles du début du XVIII^e, qui reprenant les expressions analytiques des trajectoires des planètes, et utilisant les travaux de de Moivre (1667-1754), reconnaissent le passage des cos(t) à des cosh(t),etc. et donc de l'ellipse attractive à l'hyperbole répulsive. Ces travaux sont sans doute antérieurs à ceux de Corinne (collaborateur de Clairaut ?). Cette symétrie est signalée par Appell (Traité de mécanique rationnelle) et par Whittaker (mechanics).

L'idée en tout cas est toute simple :

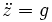si $\ddot{z} = g$ ,

en posant t' = i t et en changeant g en - g , on retrouve la même équation.

Et de fait, 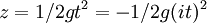$\ z = 1/2 g t^2 = -1/2 g (it)^2$ par symétrie de Corinne.

Utilisations

On la voit utilisée dans des situations diverses :

par Appell pour les fonctions de Jacobi et le pendule pesant,
plus généralement pour comparer le mouvement dans un puits de potentiel à son symétrique, la barrière de potentiel
en particulier en mécanique quantique, le passage à travers une barrière finie carrée utilise la formule de l'interféromètre de Fabry-Pérot par prolongation analytique : de la formule en 1/ [1+F.sin $φ$ ] on passe naturellement à 1/[1+ F.sh $φ$ ],
les calculs WKB et la fonction d'Airy ont aussi une symétrie de Corinne

bien sûr la formule approchée de la transmission tunnel: T = tt* = exp -[ 2 $π$ n(E)], où Wick utilise la symétrie de Corinne pour retrouver la formule de Gamow approchée.

En architecture, Antoni Gaudi, à Barcelone, va utiliser la symétrie de Corinne sans la connaître : la symétrique dans un miroir horizontal d'une chainette est évidemment la chainette renversée ; celle-ci réalise la voûte optimale qui ne nécessite aucun arc-boutant. D'où l'aspect fascinant de la Sagrada Família ou des combles de la Pedrera.

Notes et références de l'article

↑ Pour un point matériel soumis une seule force.

Voir aussi

Articles connexes

Chute avec résistance de l'air: temps de descente et temps de montée sont liés par cette symétrie
Puits de potentiel et barrière de potentiel: les mouvements s'y correspondent par cette symétrie
Pendule cycloïdal: les calculs se font jusqu'au bout pour un ovale formé de 2 cycloïdes opposées.
Pendule simple: Appell a fait remarquer que les relations entre sn(t) et sn( it) étaient des symétries de Corinne. Évidemment en aucun cas, cela ne démontre la double périodicité de sn(z), avec z variable complexe, car ici on se contente d'une transformation de fonction de variable réelle ( i.t est imaginaire pur).
Antoni Gaudi

Portail de la physique

Ce document provient de « Sym%C3%A9trie de Corinne ».

Catégories : Article à recycler (physique) | Mécanique classique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Symétrie de corinne de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

Symetrie de Corinne — Symétrie de Corinne Sommaire 1 Définition et exemple 2 Aspects historique 3 Utilisations 4 Notes et références de l article … Wikipédia en Français
Symétrie de Corinne — Sommaire 1 Définition et exemple 2 Aspects historique 3 Utilisations 4 Notes et références de l article … Wikipédia en Français
Transformation t-it — Sommaire 1 Définition et exemple 2 Aspects historiques 3 Utilisations 4 Notes et références de l article … Wikipédia en Français
Pendule cycloidal — Pendule cycloïdal Le pendule cycloïdal est le mouvement d un petit anneau de masse , soumis à la pesanteur d intensité , glissant sans frottement sur une cycloïde concave ayant pour base l axe horizontal Ox et suivant l équation : avec u… … Wikipédia en Français
Barriere de potentiel — Barrière de potentiel Le terme barrière de potentiel permet de désigner de façon intuitive les effets cinétiques que subit un objet mécanique de la part des forces auxquelles il est soumis. Notamment, dans le cas des forces répulsives son… … Wikipédia en Français
Barrière De Potentiel — Le terme barrière de potentiel permet de désigner de façon intuitive les effets cinétiques que subit un objet mécanique de la part des forces auxquelles il est soumis. Notamment, dans le cas des forces répulsives son mouvement peut être entravé,… … Wikipédia en Français
Barrière de potentiel — Le terme barrière de potentiel permet de désigner de façon intuitive les effets cinétiques que subit un objet mécanique de la part des forces auxquelles il est soumis. Notamment, dans le cas des forces répulsives son mouvement peut être entravé,… … Wikipédia en Français
Chute Avec Résistance De L'air — En physique, on désigne par chute avec résistance de l air la modélisation du problème de la chute d un corps, généralement sous atmosphère terrestre, dans laquelle on prend en compte l influence du déplacement d air sur la chute. Ce modèle est… … Wikipédia en Français
Chute avec resistance de l'air — Chute avec résistance de l air En physique, on désigne par chute avec résistance de l air la modélisation du problème de la chute d un corps, généralement sous atmosphère terrestre, dans laquelle on prend en compte l influence du déplacement d… … Wikipédia en Français
Constante des aires — Mouvement à force centrale En mécanique du point, un mouvement à force centrale est le mouvement d un point matériel soumis uniquement à une force centrale, c est à dire une force toujours dirigée vers le même point noté , appelé centre de force … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Symétrie de corinne