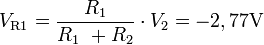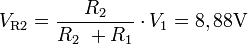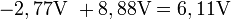Superposition linéaire

Superposition linéaire

Principe de superposition

On dit qu'un système est linéaire ou relève du principe de superposition si à la somme de deux excitations correspond la somme des deux réponses correspondantes.

Plus précisément, les excitations étant notées f (par référence aux forces de la mécanique) et les réponses x (par référence aux mouvements), le système est linéaire si :

  • la réponse 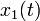x_1(t)\, étant associée à l'excitation 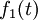f_1(t)\, et la réponse 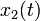x_2(t)\, associée à l'excitation f_2(t)\,,
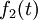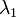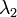  • \lambda_1\, et \lambda_2\, étant deux nombres quelconques,
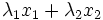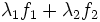  • la réponse \lambda_1 x_1 + \lambda_2 x_2\, est associée à l'excitation \lambda_1 f_1 + \lambda_2 f_2\,.

Ce résultat se généralise alors à un nombre quelconque d'excitations. En d'autres termes, si on sait décomposer une excitation en une somme de fonctions simples, il sera éventuellement possible de calculer la réponse correspondante en additionnant des réponses individuelles calculables explicitement.

En fait, les systèmes concrets possédant cette propriété sont rarissimes, pour ne pas dire inexistants. Fort heureusement, bon nombre de systèmes peuvent être raisonnablement linéarisés, soit en ignorant les petites non-linéarités dans l'hypothèse des petits mouvements (voir Systèmes oscillants à un degré de liberté), soit en procédant à une linéarisation optimisée dans le cas contraire.

En mécanique quantique, les particules atomiques peuvent exister dans plusieurs états superposés et simultanés, par exemple un électron qui peut se trouver en deux endroits à la fois, ou un photon qui passe par les deux fentes de Young en même temps.


Sommaire

Application aux circuits électriques

Dans le cas des circuits électriques composés exclusivement d'éléments linéaires (résistances, capacités, inductances, générateurs de tension ou de courant indépendants ou dépendants linéairement d'un courant, d'une tension, etc.), la réponse dans une branche est égale à la somme des réponses pour chaque générateur indépendant pris isolément, en désactivant tous les autres générateurs indépendants (générateurs de tension remplacés par des court-circuits et générateurs de courant par des circuits ouverts).

Exemple

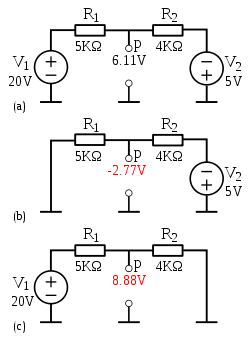
Illustration du principe de superposition.


  • En (a): La tension en P par rapport à la masse commune est de 6,11 volts. Cette valeur a été calculée en appliquant le principe de la superposition. Les étapes suivantes en font la démonstration.
  • En (b): Court-circuit de V1 pour trouver l'influence de V2. La tension entre P et la masse devient égale à la tension aux bornes de R1. On calcule cette tension avec la formule du diviseur de tension;
V_\mathrm{R1} = {R_\mathrm{1} \over R_\mathrm{1}\ + R_\mathrm{2}} \cdot V_\mathrm{2} = -2,77 \mathrm{V}
  • En (c): Court-circuit de V2 pour trouver l'influence de V1. La formule du diviseur de tension est de nouveau employée;
V_\mathrm{R2} = {R_\mathrm{2} \over R_\mathrm{2}\ + R_\mathrm{1}} \cdot V_\mathrm{1} = 8,88 \mathrm{V}

L'addition (superposition) des valeurs obtenues, nous donne bien la tension au point P de notre circuit;

-2,77 \mathrm{V}\ + 8,88 \mathrm{V} = 6,11 \mathrm{V}

On peut appliquer le même principe à des circuits utilisant plus de deux sources. Aussi, chaque diviseur de tension peut comprendre un nombre quelconque de résistances en série.

Voir aussi

Géologie

  • Portail de la physique Portail de la physique
  • Portail de l’électricité et de l’électronique Portail de l’électricité et de l’électronique
Ce document provient de « Principe de superposition ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Superposition linéaire de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Superposition — Principe de superposition quantique Cet article fait partie de la série Mécanique quantique Postulats de la mécanique quantique …   Wikipédia en Français

  • Superposition d'états — Principe de superposition quantique Cet article fait partie de la série Mécanique quantique Postulats de la mécanique quantique …   Wikipédia en Français

  • Equation lineaire — Équation linéaire Une équation à coefficients réels ou complexes est dite linéaire quand elle peut être présentée sous la forme a.x=b, où x est l inconnue, a et b sont deux nombres donnés. Si a est différent de zéro, la seule solution est le… …   Wikipédia en Français

  • Equation differentielle lineaire — Équation différentielle linéaire Une équation différentielle linéaire est un cas particulier d équation différentielle pour lequel on peut appliquer des procédés de superposition de solutions, et exploiter des résultats d algèbre linéaire. De… …   Wikipédia en Français

  • Équation différentielle linéaire — Une équation différentielle linéaire est un cas particulier d équation différentielle pour lequel on peut appliquer des procédés de superposition de solutions, et exploiter des résultats d algèbre linéaire. De nombreuses équations différentielles …   Wikipédia en Français

  • Équation linéaire — Une équation à coefficients réels ou complexes est dite linéaire quand elle peut être présentée sous la forme a.x=b, où x est l inconnue, a et b sont deux nombres donnés. Si a est différent de zéro, la seule solution est le nombre b/a. Plus… …   Wikipédia en Français

  • Systeme lineaire — Système linéaire Un système linéaire est un modèle de système qui applique un opérateur linéaire à un signal d entrée. Un système linéaire affiche typiquement des caractéristiques et des propriétés beaucoup plus simples que le cas général non… …   Wikipédia en Français

  • Système différentiel linéaire — Système linéaire Un système linéaire est un modèle de système qui applique un opérateur linéaire à un signal d entrée. Un système linéaire affiche typiquement des caractéristiques et des propriétés beaucoup plus simples que le cas général non… …   Wikipédia en Français

  • Principe de superposition — On dit qu un système est linéaire ou relève du principe de superposition si à la somme de deux excitations correspond la somme des deux réponses correspondantes. Plus précisément, si l on note les excitations ƒ (par référence aux forces de la… …   Wikipédia en Français

  • Système linéaire — Un système linéaire est un modèle de système qui applique un opérateur linéaire à un signal d entrée. Un système linéaire affiche typiquement des caractéristiques et des propriétés beaucoup plus simples que le cas général non linéaire. C est une… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”