Systeme mecanique lineaire

Dans les domaines les plus divers (mécanique, électricité,...) on rencontre des systèmes qui transforment un signal d'entrée ou excitation (une fonction d'une variable qui est généralement le temps) en un signal de sortie ou réponse. Cette transformation se fait à travers une équation différentielle ou un système différentiel contenant plusieurs équations. Si le système est régi par le principe de superposition, on parle de système linéaire. Quelle que soit la nature mathématique des équations, il peut être caractérisé par sa réponse impulsionnelle qui le décrit dans le domaine temporel. Si, ce qui est le cas général dans de nombreux domaines, ses caractéristiques restent constantes au cours du temps, on peut transformer celle-ci en fonction de transfert dans le domaine fréquentiel.

Sommaire 1 Principe de superposition 2 Réponse impulsionnelle 3 Fonction de transfert 3.1 Généralités 3.2 Cas d'une excitation sinusoïdale 3.3 Cas d'une excitation transitoire 3.4 Cas d'une excitation à variance finie 3.5 Autre expression de la fonction de transfert

Principe de superposition

On dit qu'un système est linéaire si à la somme de deux excitations correspond la somme des deux réponses correspondantes.

Plus précisément, les excitations étant notées f (par référence aux forces de la mécanique) et les réponses x (par référence aux mouvements), le système est linéaire si

• la réponse 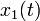étant associée à l'excitation 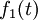et la réponse 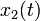associée à l'excitation ,
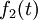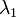• et 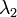étant deux nombres quelconques,
• la réponse 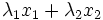est associée à l'excitation .

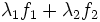Ce résultat se généralise alors à un nombre quelconque d'excitations. En d'autres termes, si on sait décomposer une excitation en une somme de fonctions simples, il sera éventuellement possible de calculer la réponse correspondante en additionnant des réponses individuelles calculables explicitement. On en verra deux exemples ci-dessous.

En fait, les systèmes concrets possédant cette propriété sont rarissimes, pour ne pas dire inexistants. Fort heureusement, bon nombre de systèmes peuvent être raisonnablement linéarisés, soit en ignorant les petites non-linéarités dans l'hypothèse des petits mouvements (voir Systèmes oscillants à un degré de liberté), soit en procédant à une linéarisation optimisée dans le cas contraire.

Réponse impulsionnelle

On peut décrire un système linéaire par sa réponse à une percussion ou impulsion, c'est-à-dire une excitation intense pendant une courte durée. Toute excitation peut être considérée comme une succession d'impulsions de faible intensité. Du fait de la linéarité, la réponse est alors une somme de réponses impulsionnelles de faible intensité décalées dans le temps. Ce raisonnement permet d'expliciter dans le domaine temporel la réponse d'un système linéaire à une excitation quelconque, au prix de calculs généralement laborieux.

L'outil mathématique correspondant est la fonction δ de Dirac ou fonction impulsion ou delta, caractérisée par l'équation suivante applicable à toute fonction f(t) suffisamment régulière :

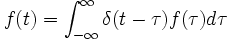
Cette somme étant utilisée pour décrire l'excitation f(t), le remplacement de l'impulsion par la réponse impulsionnelle h(t) du système linéaire permet de calculer la réponse x(t) selon la formule de Duhamel qui renvoie à la notion mathématique de convolution :

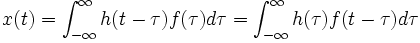
Fonction de transfert

Généralités

Au lieu de calculer explicitement la réponse du système dans le temps, il est souvent plus intéressant de déterminer son contenu en fréquences, le passage d'un domaine à l'autre se faisant à l'aide de la transformation de Fourier. On montre en mathématiques que la transformée d'une convolution est simplement le produit des transformées. En utilisant les lettres majuscules correspondantes pour ces dernières, on obtient l'équation suivante dans laquelle 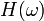s'appelle fonction de transfert du système :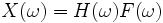

Cas d'une excitation sinusoïdale

L'énergie d'une sinusoïde est concentrée sur une seule fréquence. En termes de transformée de Fourier, elle est représentée par un delta positionné sur cette fréquence (une analyse plus rigoureuse conduit à considérer deux deltas complexes). La formule précédente transforme le delta d'entrée en un autre delta correspondant à une autre sinusoïde de même fréquence, ce qui donne la signification physique de la fonction de transfert.

D'après la linéarité, celle-ci fait donc correspondre à une somme de sinusoïdes une autre somme de sinusoïdes qui possèdent les mêmes fréquences (au contraire, un système non-linéaire crée de nouvelles fréquences). Dans le cas d'un signal périodique, il s'agit de sinusoïdes d'amplitudes finies. On considérera ci-dessous deux cas dans lesquels interviennent des sinusoïdes infiniment petites (voir à ce propos Analyse spectrale).

Cas d'une excitation transitoire

La formule précédente s'applique directement à une telle excitation, souvent dite à énergie totale finie, munie d'une transformée de Fourier.

Cas d'une excitation à variance finie

La notion de fonction de transfert s'applique aussi, au prix de quelques modifications, à une excitation par un signal à variance finie ou puissance moyenne finie, possédant une densité spectrale. La notion de processus stochastique permet alors de déterminer de manière plus ou moins précise les caractéristiques de la réponse. Si on peut supposer que l'excitation est gaussienne, la linéarité du système entraîne la même propriété pour la réponse, ce qui fournit des outils pour une description statistique précise.

Autre expression de la fonction de transfert

Dans certains domaines, on s'intéresse moins à la réponse à une excitation donnée qu'à la stabilité du système. Dans ce cas, on utilise une expression légèrement différente déduite de la transformation de Laplace.

• Portail de la physique