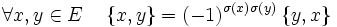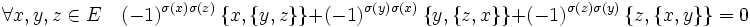Superalgèbre de lie
- Superalgèbre de lie
-
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Superalgèbre de lie de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Superalgebre de Lie — Superalgèbre de Lie Une superalgèbre de Lie est une extension de la notion d algèbre de Lie. C est la donnée d un espace vectoriel muni d une gradation σ (compatible avec la précédente décomposition), d un supercrochet de Lie vérifiant … Wikipédia en Français
Superalgèbre de Lie — Une superalgèbre de Lie est une extension de la notion d algèbre de Lie. C est la donnée d un espace vectoriel muni d une gradation σ (compatible avec la précédente décomposition), d un supercrochet de Lie vérifiant ainsi que la … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Invariance (physique) — Symétrie (physique) En physique la notion de symétrie, appelée aussi invariance, renvoie à la possibilité de considérer un même système physique selon plusieurs points de vues distincts en termes de description mais équivalents quant aux… … Wikipédia en Français
Symetrie (physique) — Symétrie (physique) En physique la notion de symétrie, appelée aussi invariance, renvoie à la possibilité de considérer un même système physique selon plusieurs points de vues distincts en termes de description mais équivalents quant aux… … Wikipédia en Français
Symétrie (physique) — En physique la notion de symétrie, appelée aussi invariance, renvoie à la possibilité de considérer un même système physique selon plusieurs points de vues distincts en termes de description mais équivalents quant aux prédictions effectuées sur… … Wikipédia en Français
Identité de Jacobi — Relation de Jacobi La relation de Jacobi est la condition nécessaire imposée sur un espace vectoriel muni d un crochet de Lie qui est une application bilinéaire antisymétrique pour en faire une algèbre de Lie. La relation de Jacobi s écrit de la… … Wikipédia en Français
Relation de Jacobi — La relation de Jacobi (ou identité de Jacobi), due à Charles Gustave Jacob Jacobi, est la condition nécessaire imposée sur un espace vectoriel muni d une application bilinéaire antisymétrique pour en faire une algèbre de Lie ; on dit alors… … Wikipédia en Français
Relation de jacobi — La relation de Jacobi est la condition nécessaire imposée sur un espace vectoriel muni d un crochet de Lie qui est une application bilinéaire antisymétrique pour en faire une algèbre de Lie. La relation de Jacobi s écrit de la façon… … Wikipédia en Français
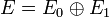 muni d'une gradation
muni d'une gradation 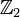 σ (compatible avec la précédente décomposition), d'un supercrochet de Lie
σ (compatible avec la précédente décomposition), d'un supercrochet de Lie 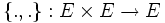 vérifiant
vérifiant