- Structure hexagonale
-
Système cristallin
Un système cristallin est un classement des cristaux sur la base de leurs caractéristiques de symétrie, sachant que la priorité donnée à certains critères plutôt qu'à d'autres aboutit à différents systèmes.
La symétrie de la maille conventionnelle permet de classer les cristaux en différentes familles cristallines : quatre dans l'espace bidimensionnel, six dans l'espace tridimensionnel.
Une classification plus fine regroupe les cristaux en différents systèmes. Il existe deux types de systèmes, selon que le critère de classification est la symétrie du réseau ou la symétrie morphologique. Historiquement, ces deux systèmes ont été indistinctement appelés système cristallin, ce qui a été à l'origine de la confusion dans la littérature surtout minéralogique.
Classification réticulaire : les systèmes réticulaires
Lorsqu'on classe les cristaux sur la base de la symétrie de leur réseau, on obtient un ensemble de quatre (espace bidimensionnel) ou sept (espace tridimensionnel) systèmes qui, dans l'ancienne littérature minéralogique francophone, (voir surtout les ouvrages de Georges Friedel) étaient appelés systèmes cristallins. Le terme officiel choisi par l'Union internationale de cristallographie est systèmes réticulaires (lattice systems en anglais)[1].
Un système réticulaire regroupe tout cristal ayant en commun le groupe ponctuel du réseau. Les tableaux suivants résument les systèmes réticulaires.
Les quatre systèmes réticulaires dans l'espace bidimensionnel symétrie du réseau système réticulaire 2 monoclinique 2mm orthorhombique 4mm tétragonal (quadratique)[2] 6mm hexagonal Les sept systèmes réticulaires dans l'espace tridimensionnel symétrie du réseau système réticulaire 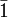
triclinique 2/m monoclinique mmm orthorhombique 4/mmm tétragonal (quadratique)[2] 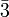 m
mrhomboédrique 6/mmm hexagonal m 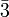 m
mcubique Trigonal versus rhomboédrique
Dans le milieu minéralogique francophone, les deux adjectifs, trigonal et rhomboédrique, sont souvent considérés comme équivalents. Pourtant le terme trigonal qualifie tout cristal ayant comme symétrie rotationnelle d'ordre maximal une rotation de ±120º autour d'un seul axe, indépendamment du type de réseau (hexagonal ou rhomboédrique) : il caractérise donc un système cristallin et non un réseau. En revanche, le terme rhomboédrique qualifie tout cristal ayant un réseau de symétrie
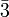 m : il caractérise cette fois un système réticulaire et non un système cristallin. La cause de cette confusion dans la littérature minéralogique est que primitivement les deux types de système étaient qualifiés de "cristallin".
m : il caractérise cette fois un système réticulaire et non un système cristallin. La cause de cette confusion dans la littérature minéralogique est que primitivement les deux types de système étaient qualifiés de "cristallin".Classification morphologique : les systèmes cristallins
La classification des cristaux sur la base de leur symétrie morphologique, ainsi que de la symétrie de leurs propriétés physiques, fut introduite par les cristallographes allemands sous le nom de système cristallin, qui a été retenu comme nom officiel par l'Union internationale de cristallographie.
Un système cristallin regroupe tout cristal caractérisé par la présence d'éléments de symétrie minimaux, auxquels peuvent éventuellement s'en ajouter d'autres jusqu'à obtenir la symétrie d'un réseau. Un cristal qui possède la pleine symétrie de son réseau est dit holoèdre ; un cristal dont la symétrie est inférieure à celle de son réseau est dit mérièdre. Les tableaux suivants résument les systèmes cristallins, où « An » signifie un point (en deux dimensions) ou un axe (en trois dimensions) de rotation de 2π/n et « m » indique une ligne (en deux dimensions) ou plan (en trois dimensions) de réflexion (miroir).
Les quatre systèmes cristallins dans l'espace bidimensionnel Élements de symétrie minimaux définissant le système cristallin système cristallin 1xA2 monoclinique 1xA2 et 2xm orthorhombique 1xA4 tétragonal (quadratique) 1xA6 hexagonal Les sept systèmes cristallins dans l'espace tridimensionnel Élements de symétrie minimaux définissant le système cristallin système cristallin 1xA1 triclinique (anortique) 1xA2 ou 1xm monoclinique 3xA2 ou 2xm + 1xA2 à leur intersection orthorhombique 1xA4 tétragonal (quadratique) 1xA3 trigonal 1xA6 hexagonal 4xA3 + 3xA2 cubique Correspondance entre systèmes et réseaux de Bravais dans l'espace tridimensionnel
Les 14 réseaux de Bravais sont définis à partir de la maille conventionnelle du réseau. Dans l'espace tridimensionnel, il existe 7 solides primitifs, qui portent les mêmes désignations que les 7 systèmes réticulaires : triclinique, monoclinique, orthorhombique, quadratique, rhomboédrique, hexagonal, cubique.
La correspondance est en revanche seulement partielle dans le cas des systèmes cristallins. Les cristaux du système trigonal peuvent avoir un réseau soit hexagonal soit rhomboédrique. Sur les 29 groupes d'espace que comptent les 5 classes trigonales, seuls 7 d'entre eux ont une maille élémentaire rhomboédrique (ce sont les groupes désignés par la lettre R ) ; les 22 autres groupes d'espace ont une maille élémentaire hexagonale (P ). Comme la maille conventionnelle du réseau rhomboédrique est hexagonale, on utilise souvent un référentiel hexagonal pour décrire les positions atomiques d'un cristal appartenant au système réticulaire rhomboédrique. Pour les 6 autres cas, la correspondance entre systèmes cristallins et systèmes réticulaires est complète.
Le tableau suivant montre les correspondances entre familles cristallines, réseaux de Bravais, systèmes réticulaires et systèmes cristallins dans l'espace tridimensionnel.
Relations entre familles cristallines, réseaux de Bravais, systèmes réticulaires et cristallins dans l'espace tridimensionnel Famille cristalline Réseaux de Bravais Système réticulaire Système cristallin Classification des groupes ponctuels Cubique cP, cF, cI Cubique Cubique 23 m3 432 -43m m-3m Hexagonale hP Hexagonal Hexagonal 6 622 6mm 6/m 6/mmm -6 -62m Hexagonale hP Hexagonal Trigonal 3 32 3m -3 -3m Hexagonale hR Rhomboédrique Trigonal 3 32 3m -3 -3m Tétragonale (quadratique) tP, tI Tétragonal (quadratique) Tétragonal (quadratique) 4 -4 422 4mm-42m 4/m 4/mmm Orthorhombique oP, oS[3], oF, oI Orthorhombique Orthorhombique 222 mm2 mmm Monoclinique mP, mS[3] Monoclinique Monoclinique 2 m 2/m Triclinique aP Triclinique Triclinique 1 -1 Les systèmes cristallins et leurs propriétés
Système
groupes d'espaceClasse de symétrie Formes cristallines Symétries Symboles
d'Hermann-
Mauguinaxes 2π/ pla
nscen
tre2 3 4 6 triclinique
1-2hémiédrie formes à une seule face - - - - - - 1 holoédrie pinacoïde - - - - - oui 
monoclinique
3-15hémiédrie axiale dôme, ou dièdre 1 - - - - - 2 antihémiédrie dôme - - - - 1 - m holoédrie prisme 1 - - - 1 oui 2/m ortho-
rhombique
16-74hémiédrie holoaxe tétraèdre orthorhombique 3 - - - - - 2 2 2 antihémiédrie pyramide orthorhombique 1 - - - 2 - m m 2 holoédrie octaèdre orthorhombique 3 - - - 3 oui 2/m 2/m 2/m quadratique ou
tétragonal
75-142tétartoèdrie énantiomorphe pyramide tétragonale - - 1 - - - 4 tétartoédrie sphénoédrique disphénoèdre tétragonal 1 - - - - - 
parahémiédrie dipyramide tétragonale - - 1 - 1 oui 4/m hémiédrie holoaxe trapézoèdre tétragonal 4 - 1 - - - 4 2 2 antihémiédrie pyramide ditétragonale - - 1 - 4 - 4 m m hémiédrie sphénoédrique scalénoèdre tétragonal 3 - - - 2 -  2 m
2 mholoédrie dipyramide ditétragonale 4 - 1 - 5 oui 4/m 2/m 2/m trigonal
143-167ogdoédrie hexagonale pyramide trigonale - 1 - - - - 3 tétartoédrie rhomboédrique paratétartoédrie (hexagonale) rhomboèdre - 1 - - - oui 
parahémiédrie (rhomboédrique) tétartoédrie (hexagonale) trapézoèdre trigonal 3 1 - - - - 3 2 hémiédrie holoaxe (rhomboédrique) antitétardoédrie (hexagonale) pyramide ditrigonale - 1 - - 3 - 3 m antihémiédrie (rhomboédrique) parahémiédrie trigonal
(réseau hexagonal)scalénoèdre - rhomboèdre 3 1 - - 3 oui  2/m
2/mholoédrie
(réseau rhomboédrique)hexagonal
168-194tétartoédrie énantiomorphe pyramide hexagonale - - - 1 - - 6 tétartoédrie triangulaire dipyramide triangulaire - 1 - - 1 - 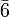 [4]
[4]parahémiédrie dipyramide hexagonale - - - 1 1 oui 6/m hémiédrie holoaxe trapézoèdre hexagonal 6 - - 1 - - 6 2 2 antihémiédrie pyramide dihexagonale
pyramide hexagonale- - - 1 6 - 6 m m hémiédrie triangulaire dipyramide/prisme ditrigonal 3 1 - - 4 - 6 m 2 holoédrie dipyramide dihexagonale 6 - - 1 7 oui 6/m 2/m 2/m cubique
ou
isométrique
195-230tétartoédrie pentagonotritétraèdre 3 4 - - - - 2 3 parahémiédrie diploèdre - dodécaèdre 3 4 - - 3 oui 2/m 
hémiédrie holoaxe pentagonotrioctaèdre 6 4 3 - - - 4 3 2 antihémiédrie de l'hexatétraèdre au tétraèdre 3 4 - - 6 -  3 m
3 mholoédrie de l'hexooctaèdre au cube 6 4 3 - 9 oui 4/m 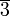 2/m
2/mLes 230 types de groupes d'espace
Note. Le plan de type e est un plan avec double glissement, le long de deux directions différentes, qui existe dans cinq types de groupes d'espace à réseau centré. L'utilisation du symbole e est devenue officielle à compter de la cinquième édition du volume A des Tables internationales de cristallographie (2002).
Classe # système triclinique 1 1 P1 
2 P 
système monoclinique 2 3-5 P2 P21 C2 m 6-9 Pm Pc Cm Cc 2/m 10-15 P2/m P21/m C2/m P2/c P21/c C2/c système orthorhombique 222 16-24 P222 P2221 P21212 P212121 C2221 C222 F222 I222 I212121 mm2 25-46 Pmm2 Pmc21 Pcc2 Pma2 Pca21 Pnc2 Pmn21 Pba2 Pna21 Pnn2 Cmm2 Cmc21 Ccc2 Amm2 Aem2 Ama2 Aea2 Fmm2 Fdd2 Imm2 Iba2 Ima2 mmm 47-74 Pmmm Pnnn Pccm Pban Pmma Pnna Pmna Pcca Pbam Pccn Pbcm Pnnm Pmmn Pbcn Pbca Pnma Cmcm Cmce Cmmm Cccm Cmme Ccce Fmmm Fddd Immm Ibam Ibca Imma système quadratique ou tétragonal 4 75-80 P4 P41 P42 P43 I4 I41 
81-82 P 
I 
4/m 83-88 P4/m P42/m P4/n P42/n I4/m I41/a 422 89-98 P422 P4212 P4122 P41212 P4222 P42212 P4322 P43212 I422 I4122 4mm 99-110 P4mm P4bm P42cm P42nm P4cc P4nc P42mc P42bc I4mm I4cm I41md I41cd  2m
2m111-122 P  2m
2mP  2c
2cP  21m
21mP  21c
21cP  m2
m2P  c2
c2P  b2
b2P  n2
n2I  m2
m2I  c2
c2I  2m
2mI  2d
2d4/mmm 123-142 P4/mmm P4/mmc P4/nbm P4/nnc P4/mbm P4/nnc P4/nmm P4/ncc P42/mmc P42/mcm P42/nbc P42/nnm P42/mbc P42/mnm P42/nmc P42/ncm I4/mmm I4/mcm I41/amd I41/acd système trigonal 3 143-146 P3 P31 P32 R3 
147-148 P 
R 
32 149-155 P312 P321 P3112 P3121 P3212 P3221 R32 3m 156-161 P3m1 P31m P3c1 P31c R3m R3c  m
m162-167 P  1m
1mP  1c
1cP  m1
m1P  c1
c1R  m
mR  c
csystème hexagonal 6 168-173 P6 P61 P65 P62 P64 P63 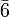
174 P 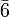
6/m 175-176 P6/m P63/m 622 177-182 P622 P6122 P6522 P6222 P6422 P6322 6mm 183-186 P6mm P6cc P63cm P63mc 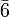 m2
m2187-190 P 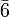 m2
m2P 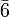 c2
c2P 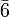 2m
2mP 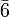 2c
2c6/mmm 191-194 P6/mmm P6/mcc P63/mcm P63/mmc système cubique 23 195-199 P23 F23 I23 P213 I213 m 
200-206 Pm 
Pn 
Fm 
Fd 
I 
Pa 
Ia 
432 207-214 P432 P4232 F432 F4132 I432 P4332 P4132 I4132  3m
3m215-220 P  3m
3mF  3m
3mI  3m
3mP  3n
3nF  3c
3cI  3d
3dm  m
m221-230 Pm  m
mPn  n
nPm  n
nPn  m
mFm  m
mFm  c
cFd  m
mFd  c
cIm  m
mIa  d
dTermes utilisés en cristallographie
- un diploèdre est une combinaison de deux rhomboèdres.
- ditétragonale qualifie une forme construite sur une base à 8 côtés.
- ditrigonale qualifie une forme construite sur une base à 6 côtés.
- un dodécaèdre est un cristal à douze faces ; les faces sont des pentagones dans le cas d'un dodécaèdre régulier.
- énantiomorphe qualifie un cristal qui comporte des éléments appariés de même forme, mais symétriquement inversés.
- l'holoédrie est la propriété d'un cristal dont la symétrie est exactement celle du réseau périodique qui lui correspond.
- la mériédrie est la propriété d'un cristal dont la symétrie est inférieure à celle du réseau périodique qui lui correspond. Elle est divisée en:
- hémiédrie, ou mériédrie d'ordre 2
- tétartoédrie, ou mériédrie d'ordre 4
- ogdoédrie, ou mériédrie d'ordre 8
- holoaxe qualifie un cristal qui possède tous ses axes de symétrie.
- une pinacoïde est une forme « ouverte » délimitée par 2 faces parallèles.
- un rhomboèdre est un parallélépipède dont les faces sont des losanges.
- un scalénoèdre est un polyèdre irrégulier à faces scalènes, c'est-à-dire qui forment des triangles dont les trois côtés sont inégaux.
- un sphénoèdre est un polyèdre à faces aiguës se croisant deux à deux en coins.
- tétragonale qualifie une forme construite sur une base à 4 côtés.
- Un trapézoèdre est un solide dont les faces sont des trapèzes.
- trigonale qualifie une forme construite sur une base à 3 côtés.
Voir aussi l'article forme cristalline
Notes
- ↑ Dans les Tables internationales de cristallographie publiées avant 2002 les systèmes réticulaires étaient appelés « systèmes de Bravais ».
- ↑ a et b L’adjectif d'origine latine quadratique est plus utilisé en français que l'adjectif d'origine grecque tétragonal. Toutefois, ce dernier est l'adjectif standard utilisé dans les Tables internationales de cristallographie. Par ailleurs, les symboles des réseaux de Bravais dans cette famille utilisent la première lettre t de l'adjectif tétragonal.
- ↑ a et b «S » signifie une seule paire de faces centrées.
- ↑ L'opération
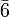 est équivalente à 3/m ; toutefois, la notation 3/m reviendrait à placer le groupe correspondant dans le système cristallin trigonal, avec deux réseaux possibles, alors que ce groupe n'est compatible qu'avec le réseau hexagonal.. Pour cette raison, seule la notation
est équivalente à 3/m ; toutefois, la notation 3/m reviendrait à placer le groupe correspondant dans le système cristallin trigonal, avec deux réseaux possibles, alors que ce groupe n'est compatible qu'avec le réseau hexagonal.. Pour cette raison, seule la notation 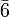 est acceptée.
est acceptée.
Voir aussi
Articles connexes
Liens externes
- (en) Les groupes d'espace
- Portail de la chimie
- Portail de la physique
- Portail des minéraux et roches
Catégorie : Cristallographie
Wikimedia Foundation. 2010.
