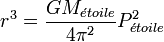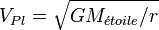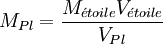Spectroscopie Doppler

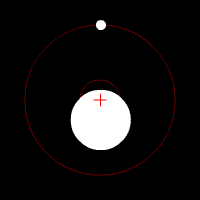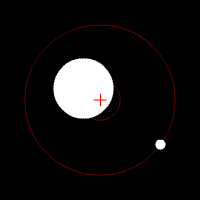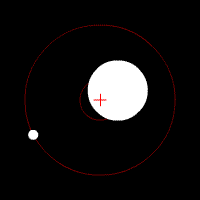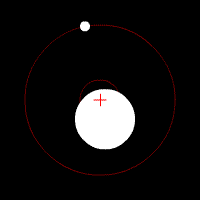Diagramme montrant l'influence d'un petit objet (comme une planète) orbitant autour d'un autre, beaucoup plus massif (comme une étoile). Le petit corps produit en effet des changement de vélocité sur le plus grand, de telle sorte que les deux objet semblent graviter autour d'un barycentre commun (croix rouge).

La méthode des vitesses radiales (également appelée la spectroscopie Doppler) est une méthode spectroscopique utilisée dans la recherche d'exoplanètes. Elle implique l'observation de l'effet Doppler-Fizeau dans le spectre de l'étoile autour de laquelle une planète orbite.

Il est extrêmement difficile d'observer une planète extra solaire directement. Le rayonnement indirect de la planète est très faible, comparé au rayonnement direct de son étoile, avec les distances interstellaires, nos télescopes sont ébloui par le rayonnement de l'étoile. D'ailleurs, les premières observations directes remontent seulement à 2004 et 2005. Par conséquent, la majorité des exoplanètes sont détectées en utilisant des méthodes indirectes, telle la spectroscopie Doppler. Presque toutes les planètes extra solaires connues à ce jour ont été découvertes grâce à cette méthode.

Historique

Otto Struve proposa en 1952 d'utiliser de puissant spectromètres pour détecter des planètes lointaines. Il décrivit comment une planète géante, comme Jupiter pouvait provoquer de légères oscillations auprès de son étoile, comme deux objets célestes gravitant autour d'un barycentre commun^[1]. Il prédit que la lumière émise par l'étoile subirait de petits changements dus à l'effet Doppler, eux-mêmes causés par des variations périodiques de la vitesse radiale de l'étoile. Ces variations seraient détectable par un spectromètre très sensible, et se traduiraient comme une alternance de redshifts et de blueshifts très légers sur la lumière de l'étoile. Cependant, les instruments de l'époque ne pouvaient mesurer la vitesse radiale d'un objet qu'avec une marge d'erreur de 1000 m/s ou plus, ce qui les rendaient inutiles dans la détection de nouvelles planètes^[2]. Les changements de vitesse radiale attendus sont en très petit - Jupiter cause au Soleil un changement de 13 m/s sur une période de 12 ans, et la Terre une changement de 0,1 m/s sur une période de 1 an - ce qui implique des observations à long terme avec des instruments de très haute résolution^[2].

Les progrès des technologies de spectromètrie et d'observation effectués durant les années 80 et 90 ont abouti à des instruments capable de tels recherches. La première exoplanète jamais découverte, 51 Pegasi b, fut détectée en Octobre 1995 en utilisant la spectroscopie Doppler^[3]. Depuis, plus de 200 planètes extrasolaires ont été identifiées, et la plupart grâce des programmes de recherches basés au Keck, au Lick et à d'autres observatoires Anglo-Australiens, ainsi que des équipes basées au Geneva Extrasolar Planet Search, en utilisant la méthodes des vitesses radiales^[3].

Méthode

Une série d'observations sont effectuées sur le spectre de la lumière émise par l'étoile. Des variations dans ce spectre peuvent être détectée, lorsque la longueur d'onde de certaines raies d'absorption spectrales augmente et diminue de façon régulière sur un intervalle de temps donné. Ces variations peuvent être révélatrices de changements dans la vitesse radiale, celle-ci pouvant être altérée par la présence d'une planète en orbite autour de l'étoile, causant l'effet Doppler-Fizeau sur la lumière émise par l'étoile.

Si une planète extrasolaire est détectée, sa masse peut être déterminée à partir des changements de vitesse radiale de son étoile. Un graphique de la vitesse radiale, mesurée par rapport au temps donnera une courbe caractéristique (courbe sinusoïdale dans le cas d'une orbite circulaire), et l'amplitude de la courbe permettra de calculer la masse de la planète.

Exemple

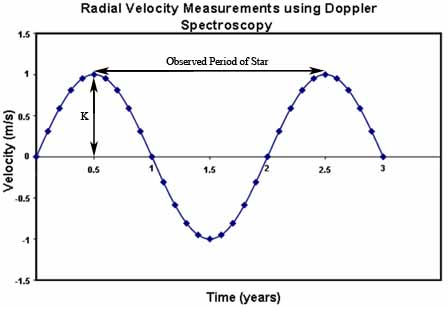
Le graphique à droite illustre la courbe sinusoïdale créée en utilisant la spectroscopie Doppler pour observer une étoile imaginaire autour de laquelle graviterait une planète sur une orbite circulaire. Des observations sur une étoile réelle engendrerait une graphe similaire, bien que l'excentricité orbitale déformerait la courbe et compliquerait les calculs ci-dessous.

La vitesse de l'étoile théorique montre une variation périodique de ± 1 m/s, suggérant une masse qui est en orbite autour d'elle.E n utilisant la troisième loi de Kepler, la période observée de l'orbite de la planète autour de l'étoile (correspondant à la période à laquelle le spectre de l'étoile se modifie) peut être utilisée afin de déterminer la distance séparant la planète de l'étoile. Ceci peut se faire grâce à l'équation suivante :

où

• r est la distance séparant la planète de l'étoile,
• G est la constante gravitationnelle,
• M_etoile est la masse de l'étoile,
• P_etoile est la période citée plus haute.

Ayant à présent déterminé r, la vélocité de la planète autour de l'étoile peut être calculée en utilisant la loi de Newton sur la gravitation :

où V_Pl est la vélocité de la planète.

La masse de la planète peut alors être calculée à partir de sa vélocité :

où V_etoile est la vélocité observée de l'étoile principale. La vélocité Doppler observée, K = V_etoilesin(i), où i est l'inclinaison de l'orbite de la planète par rapport à la ligne de visée.

Ainsi, en supposant qu'on ait une valeur pour l'inclinaison de la planète et pour la masse de l'étoile, les changements dans la vitesse radiale de l'étoile peuvent être utilisée pour calculer la masse d'une exoplanète.

Problèmes

Le problème majeur inhérent à la méthode est qu'il mesure uniquement le mouvement de l'étoile sur la ligne de mire, et dépend donc de l'inclinaison de l'orbite de la planète ; dans le cas ou celle-ci est inconnue, il devient plus difficile de déterminer exactement la masse de la planète. Si le plan orbital de la planète se situe bel et bien alignée avec la ligne de mire de l'observateur, les variations de la vitesse radiale mesurées correspondent alors à la vraie valeur. Dans le cas contraire, lorsque le plan orbital et la ligne de mire ne sont pas alignés, l'effet que la planète a sur l'étoile sera en réalité plus grand que ce qui a été mesuré à travers les changements de vitesse radiale de l'étoile. Par conséquent, la vraie masse de la planète sera plus grande que prévue.

Afin de corriger cet inconvénient, et déterminer par la même occasion la vrai masse de l'exoplanète, les mesures de vitesse radiale doivent être combinées avec des mesures astrométriques. Celle-ci suivront le mouvement propre de la planète dans le plan du ciel, qui est perpendiculaire à la ligne de visée. Ces mesures astrométriques permettent aux chercheurs de vérifier si des objets qui semblent être des planètes de masse élevée ne sont pas plutôt des naines brunes^[2].

Un autre problème est que l'enveloppe de gaz peut se dilater et se contracter (de manière périodique dans certains cas), et certaines étoiles sont variables. La spectroscopie Doppler ne convient pas pour trouver des planètes autour de ce type d'étoile, parce que de tels changements dans le spectre de l'étoile peuvent masquer le petit effet causé par la planète.

Cette méthode est la meilleure pour détecter des objets très massifs orbitant près de leur étoile, appelés Jupiters chauds, qui ont un fort effet gravitationnel sur l'étoile et causent donc de grand changements dans sa vitesse radiale. L'observation de nombreuses raies spectrales et de nombreuses périodes orbitale permet d'augmenter le rapport signal sur bruit des observations, ce qui amplifie les changements causés par une planète plus petite ou plus lointaine ; mais la détection de planètes telluriques similaires à la Terre reste impossible avec les instruments actuels.

Notes et références

• (en) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en anglais intitulé « Doppler spectroscopy »..

Voir aussi

Articles connexes

• Effet Doppler-Fizeau
• Vitesse radiale
• Exoplanète

Liens externes

• Informations supplémentaires

• Portail de l’astronomie