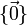Sous-groupes triviaux
- Sous-groupes triviaux
-
Sous-groupes triviaux
Soit G un groupe, on appelle sous-groupes triviaux de G :
- Le groupe constitué de l'élément neutre
- Le groupe G lui-même
Sous groupe vectoriel triviaux
Soit E un espace vectoriel.
Les deux sous-espaces vectoriels :
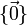
- E
sont qualifiés de triviaux.
Ce sont aussi les sous-groupes triviaux de E pour l'addition
Voir aussi
Catégorie : Groupe remarquable
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Sous-groupes triviaux de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Sous-espaces vectoriels triviaux — Sous groupes triviaux Soit G un groupe, on appelle sous groupes triviaux de G : Le groupe constitué de l élément neutre Le groupe G lui même Sous groupe vectoriel triviaux Soit E un espace vectoriel. Les deux sous espaces vectoriels : E … Wikipédia en Français
Sous-groupe — Un sous groupe est un objet mathématique décrit par la théorie des groupes. Dans cet article, désigne un groupe d élément neutre . Sommaire 1 Définitions 1.1 Sous groupe propre … Wikipédia en Français
GROUPES (mathématiques) - Groupes finis — Née de l’étude des groupes de permutations des racines d’équations, la théorie des groupes finis s’est développée indépendamment depuis le Traité des substitutions et des équations algébriques (1870) de Camille Jordan. Après les travaux… … Encyclopédie Universelle
GROUPES (mathématiques) - Généralités — On se propose de présenter ici les notions fondamentales de théorie des groupes qui interviendront constamment dans la suite des articles qui traitent des groupes. Ces articles contiennent un très grand nombre d’exemples, c’est pourquoi cet… … Encyclopédie Universelle
Groupes finis simples — Liste des groupes finis simples En mathématiques, la classification des groupes finis simples établit que chacun de ces groupes est soit un cyclique, soit alterné, soit membre d une des seize familles de groupes de type de Lie (incluant le groupe … Wikipédia en Français
Ideaux triviaux — Idéaux triviaux Soit A un anneau de neutre 0, les idéaux triviaux de A sont : {0} A Ce sont aussi les sous groupes triviaux de A vu comme groupe additif. Un anneau commutatif dont les seuls idéaux sont triviaux est un corps. Un anneau dont… … Wikipédia en Français
Idéaux Triviaux — Soit A un anneau de neutre 0, les idéaux triviaux de A sont : {0} A Ce sont aussi les sous groupes triviaux de A vu comme groupe additif. Un anneau commutatif dont les seuls idéaux sont triviaux est un corps. Un anneau dont les seuls idéaux… … Wikipédia en Français
Idéaux triviaux — Soit A un anneau de neutre 0, les idéaux triviaux de A sont : {0} A Ce sont aussi les sous groupes triviaux de A vu comme groupe additif. Un anneau commutatif dont les seuls idéaux sont triviaux est un corps commutatif. Un anneau non… … Wikipédia en Français
Liste Des Groupes Finis Simples — En mathématiques, la classification des groupes finis simples établit que chacun de ces groupes est soit un cyclique, soit alterné, soit membre d une des seize familles de groupes de type de Lie (incluant le groupe de Tits), soit l un des 26… … Wikipédia en Français
Liste des groupes finis simples — En mathématiques, la classification des groupes finis simples établit que chacun de ces groupes est soit un cyclique, soit alterné, soit membre d une des seize familles de groupes de type de Lie (incluant le groupe de Tits), soit l un des 26… … Wikipédia en Français