Semianneau

En mathématiques, un semi-anneau, ou un demi-anneau, est une structure algébrique 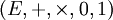telle que

• (E, + ,0) constitue un monoïde commutatif;
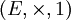• forme un monoïde;
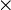• est distributif par rapport à +;
• 0 est absorbant pour le produit, autrement dit: pour tout .

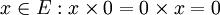Un demi-anneau est commutatif quand son produit est commutatif.

Remarque: un anneau se construit de façon similaire à partir d'un groupe additif et d'un monoïde multiplicatif mais il n'a pas besoin du dernier axiome car l'absorption du zéro se déduit de l'inversibilité de la somme.

Domaines de prédilection

Les demi-anneaux se retrouvent souvent en:

• recherche opérationnelle: les graphes ont des poids dans un demi-anneau; le produit est associé à l'accumulation de valeur le long d'un chemin et la somme correspond à la façon de composer plusieurs chemins;
• théorie des langages et des automates: la concaténation des (ensembles de) chaînes pour en fabriquer d'autres est le produit et l'union des (ensembles de) chaînes est la somme.

Exemples

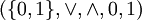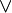• Le demi-anneau le plus simple est celui des booléens: où et sont OU et ET respectivement.
• Le plus naturel est peut-être celui des entiers positifs avec l'addition et la multiplication: .
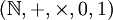• L'ensemble des entiers naturels étendu à 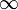de façon habituelle (toute somme avec 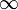donne 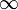; tout produit avec 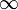donne 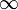, sauf pour 0 qui reste absorbant) muni de l'opérateur min et de la somme est un demi-anneau: 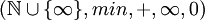est connu sous le nom de demi-anneau tropical; il est au cœur des algorithmes de calcul de plus court chemin dans un graphe: les poids sont additionnés le long des chemins et devant plusieurs chemins, on prend le coût minimal.
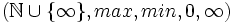• est le demi-anneau sous-jacent au calcul du flux maximum d'un graphe: dans une séquence d'arcs, celui de poids minimal impose son flux et devant plusieurs séquences, on prend le flux maximal.
• L'ensemble des parties d'un ensemble E muni de l'union et de l'intersection est un semi-anneau. Les deux lois sont distributives l'une par rapport à l'autre, l'élément neutre de l'union est l'ensemble vide, celui de l'intersection est l'ensemble E. Les deux lois sont commutatives et forment avec E les deux monoïdes requis. C'est une algèbre de Boole et donc un treillis.
• Tout treillis distributif est un semi-anneau.

• Portail des mathématiques