Seconde vitesse cosmique

Seconde vitesse cosmique

Vitesse cosmique

En 1883, l'écrivain russe Konstantin Tsiolkovsky présentait dans son ouvrage L’Espace libre les concepts fondamentaux pour la construction de fusées à réaction comme unique moyen de quitter la gravité terrestre.

Tsiolkovsky introduisait trois vitesses minimales théoriques appelées respectivement première, deuxième et troisième vitesse cosmique.

Ces notions peuvent se généraliser à toute planète d'un système solaire.

Sommaire

Cas de la Terre

Première vitesse cosmique

La première vitesse cosmique représente la vitesse de satellisation minimale autour de la Terre. Vitesse minimale qu’il faut théoriquement communiquer à un corps, au départ de la Terre, pour le satelliser autour d’elle en orbite basse. Elle est déterminée par la relation

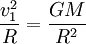\frac{v_1^2}{R} = \frac{G M}{R^2},

où :

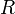  • {R} \ est le rayon de l'orbite, assimilé au rayon terrestre (6370 km, bien qu'en en réalité une orbite n'échappe à l'usure de l'atmosphère terrestre que si elle est à une altitude supérieure à 200 kilomètres),
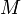  • {M} \ est la masse de la Terre (environ 6×1024 kg),
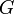  • {G} \ est la constante de gravitation.

Cette relation signifie que la force de gravitation exercée par la Terre (GMm / R2, m étant la masse de la fusée) est exactement compensée par la force centrifuge (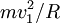m v_1^2 / R) de la fusée quand celle-ci est en orbite circulaire.

La première vitesse cosmique vaut ainsi

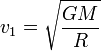
v_1 = \sqrt{\frac{G M}{R}}

soit environ

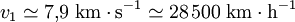v_1 \simeq 7,\!9\;{\rm km}\cdot{\rm s}^{-1} \simeq 28\,500\;{\rm km}\cdot{\rm h}^{-1} .

Deuxième vitesse cosmique

La deuxième vitesse cosmique correspond à la vitesse de libération d’un corps quittant la Terre. C’est la vitesse minimale au-delà de laquelle un corps peut s’éloigner définitivement de la Terre, en tout cas tant que l'on néglige la présence du Soleil et de notre Galaxie. Elle est déterminée, avec les mêmes notations que précédemment, par la relation

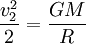\frac{v_2^2}{2} = \frac{G M}{R},

équation qui décrit que la somme de l'énergie cinétique et de l'énergie potentielle de gravitation se compensent, conférant une énergie totale nulle à la fusée, condition nécessaire à ce qu'elle puisse s'échapper de l'attraction terrestre.

La deuxième vitesse cosmique vaut ainsi :

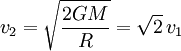
v_2 = \sqrt{\frac{2 G M}{R}} = \sqrt{2}\, v_1

soit environ

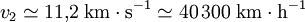v_2 \simeq 11,\!2\;{\rm km}\cdot{\rm s}^{-1} \simeq 40\,300\;{\rm km}\cdot{\rm h}^{-1} .

À noter qu'ici, il n'y a pas d'ambiguité sur la quantité R qui correspond au rayon terrestre, puisque c'est de là qu'est lancée la fusée, contrairement à la première vitesse cosmique où la quantité R était censée représenter le rayon d'une orbite basse, légèrement supérieur (d'environ 3%) au rayon terrestre. La vitesse de libération augmente avec la compacité de l'objet, c'est-à-dire son rapport M/R. Par exemple, celle de Jupiter est de 59,5 km/s.

Troisième vitesse cosmique

La troisième vitesse cosmique est définie comme étant la vitesse de libération d’un corps quittant le système solaire depuis l'orbite terrestre. Elle est déterminée de la même façon que la seconde vitesse cosmique, si ce n'est qu'il faut tenir compte de l'énergie potentielle de gravitation de la Terre et du Soleil, et du fait que la Terre est elle-même animée d'une certaine vitesse vT sur son orbite. Ainsi,

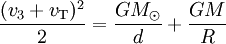\frac{(v_3 + v_{\rm T})^2}{2} = \frac{G M_\odot}{d} + \frac{G M}{R},

où :

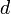  • {d} \ correspondant à la distance Terre-Soleil, soit une unité astronomique (environ 150 millions de kilomètres) et,
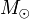  • {M_\odot} correspond à la masse du Soleil.

Or la vitesse de la Terre sur son orbite correspond à la première vitesse cosmique du Soleil pour une distance d'une unité astronomique, soit

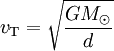v_{\rm T} = \sqrt{\frac{G M_\odot}{d}}.

Par conséquent :

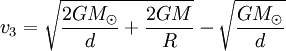
v_3 = \sqrt{\frac{2 G M_\odot}{d} + \frac{2 G M}{R}} - \sqrt{\frac{G M_\odot}{d}}

L'application numérique donne alors

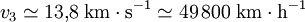v_3 \simeq 13,\!8\;{\rm km}\cdot{\rm s}^{-1} \simeq 49\,800\;{\rm km}\cdot{\rm h}^{-1} .

Cas général

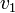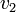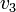Les formules littérales ci-dessus, donnant {v_1} \ , {v_2} \ , et {v_3} \ sont applicables dans le contexte plus général d'une planète située dans un système solaire.

Dans ce cas :

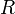  • {R} \ est le rayon de l'orbite, au moins égal au rayon de la planète, augmenté éventuellement de l'épaisseur de son atmosphère si on veut échapper au frottement.
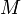  • {M} \ est la masse de la planète d'où est lancé le projectile.
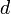  • {d} \ correspondant à la distance entre la planète et son soleil.
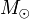  • {M_\odot} est la masse du soleil autour duquel tourne la planète d'où est lancé le projectile.
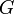  • {G} \ est la constante de gravitation, qui est réputée garder la même valeur dans tout notre univers.

Voir aussi

  • Portail de l’astronautique Portail de l’astronautique
  • Portail de l’astronomie Portail de l’astronomie
Ce document provient de « Vitesse cosmique ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Seconde vitesse cosmique de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Vitesse cosmique — En 1883, l écrivain russe Konstantin Tsiolkovsky présentait dans son ouvrage L’Espace libre les concepts fondamentaux pour la construction de fusées à réaction comme unique moyen de quitter la gravité terrestre. Tsiolkovsky introduisait trois… …   Wikipédia en Français

  • Deuxième vitesse cosmique — Vitesse cosmique En 1883, l écrivain russe Konstantin Tsiolkovsky présentait dans son ouvrage L’Espace libre les concepts fondamentaux pour la construction de fusées à réaction comme unique moyen de quitter la gravité terrestre. Tsiolkovsky… …   Wikipédia en Français

  • Première vitesse cosmique — Vitesse cosmique En 1883, l écrivain russe Konstantin Tsiolkovsky présentait dans son ouvrage L’Espace libre les concepts fondamentaux pour la construction de fusées à réaction comme unique moyen de quitter la gravité terrestre. Tsiolkovsky… …   Wikipédia en Français

  • Troisième vitesse cosmique — Vitesse cosmique En 1883, l écrivain russe Konstantin Tsiolkovsky présentait dans son ouvrage L’Espace libre les concepts fondamentaux pour la construction de fusées à réaction comme unique moyen de quitter la gravité terrestre. Tsiolkovsky… …   Wikipédia en Français

  • Vitesse d'evasion — Vitesse de libération Illustration du raisonnement d Isaac Newton. Depuis le sommet d une montagne, un canon envoie des projectiles avec chaque fois plus de puissance. Les projectiles A et B retombent sur terre. Le projectile C entre en orbite… …   Wikipédia en Français

  • Vitesse d'échappement — Vitesse de libération Illustration du raisonnement d Isaac Newton. Depuis le sommet d une montagne, un canon envoie des projectiles avec chaque fois plus de puissance. Les projectiles A et B retombent sur terre. Le projectile C entre en orbite… …   Wikipédia en Français

  • Vitesse d'évasion — Vitesse de libération Illustration du raisonnement d Isaac Newton. Depuis le sommet d une montagne, un canon envoie des projectiles avec chaque fois plus de puissance. Les projectiles A et B retombent sur terre. Le projectile C entre en orbite… …   Wikipédia en Français

  • Vitesse de fuite — Vitesse de libération Illustration du raisonnement d Isaac Newton. Depuis le sommet d une montagne, un canon envoie des projectiles avec chaque fois plus de puissance. Les projectiles A et B retombent sur terre. Le projectile C entre en orbite… …   Wikipédia en Français

  • Vitesse de liberation — Vitesse de libération Illustration du raisonnement d Isaac Newton. Depuis le sommet d une montagne, un canon envoie des projectiles avec chaque fois plus de puissance. Les projectiles A et B retombent sur terre. Le projectile C entre en orbite… …   Wikipédia en Français

  • Vitesse parabolique — Vitesse de libération Illustration du raisonnement d Isaac Newton. Depuis le sommet d une montagne, un canon envoie des projectiles avec chaque fois plus de puissance. Les projectiles A et B retombent sur terre. Le projectile C entre en orbite… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”