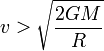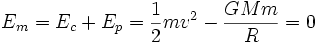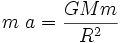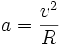Vitesse d'évasion

Illustration du raisonnement d'Isaac Newton. Depuis le sommet d'une montagne, un canon envoie des projectiles avec chaque fois plus de puissance. Les projectiles A et B retombent sur terre. Le projectile C entre en orbite circulaire, D en orbite elliptique. Le projectile E se libère de l'attraction terrestre.

La vitesse de libération (aussi appelée vitesse d'évasion, vitesse parabolique, vitesse de fuite, ou vitesse d'échappement, en anglais escape velocity) d'une planète est la vitesse qui, si elle est impartie à un objet à la surface de cette planète, conduira à ce qu'il échappe définitivement à l'attraction gravitationnelle de cette planète (ceci en supposant négligeable la résistance de l'atmosphère). Formulé autrement , c'est la vitesse minimale que doit atteindre théoriquement un corps pour s'éloigner indéfiniment d'un astre malgré l'attraction gravitationnelle de ce dernier. La vitesse de libération d'une planète est aussi la vitesse qu'un corps, initialement au repos et à distance infinie, acquiert en tombant jusqu'à la surface de la planète.

La vitesse de libération se calcule d'après la formule suivante :

Où G est la constante gravitationnelle universelle (6,6742×10^-11 m³·kg^-1·s^-2), M est la masse de la planète, et R son rayon. La vitesse de libération augmente ainsi lorsque la masse de la planète augmente et aussi lorsque son rayon diminue.

Démonstration de la relation

On part du principe selon lequel l'énergie mécanique d'un corps est constante au cours du temps. À la distance R, la vitesse du corps est la vitesse de libération. À une distance infinie, sa vitesse et son énergie potentielle de gravitation sont nulles. Son énergie mécanique est donc nulle.

Les masses se simplifient et on obtient la formule indiquée.

Comme par définition, la vitesse de libération est la vitesse nécessaire pour se soustraire complètement à la gravité d'une planète ou plus généralement d'un corps quelconque à partir de sa surface, celle-ci est plus élevée que la vitesse de mise en orbite puisque un corps en orbite subit encore la gravité du corps en question. La vitesse de mise en orbite est:

Pour le montrer, appliquer le principe fondamental de la dynamique au satellite à mettre en orbite :

Dans le Repère de Frenet lié au satellite en orbite, l'accélération normale s'écrit:

Les masses se simplifient à nouveau et on obtient bien la formule annoncée.

A noter qu'un corps en altitude requiert une vitesse inférieure à celle de libération pour se soustraire à la gravité. La vitesse requise est dans ce cas obtenue par la formule :

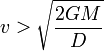où D est la distance au centre de la planète ou du corps dont l'on souhaite se libérer.

Valeurs remarquables de vitesse de libération

La vitesse de libération d'un corps quittant la surface de la Terre, dite aussi deuxième vitesse cosmique, est de l'ordre de 11,2 kilomètres par seconde (soit environ 40 000 km/h) par rapport à un repère inertiel géocentrique. Par comparaison, celle de Jupiter est de 59,5 km/s. La sonde Luna 1 fut, en 1959, le premier objet construit par l'homme à atteindre la vitesse de libération terrestre lors de son trajet en direction de la Lune.

La vitesse de libération d'un corps quittant le système solaire, dite aussi troisième vitesse cosmique, est de l'ordre de 16,6 kilomètres par seconde par rapport à un repère inertiel géocentrique.

Remarques

Contrairement à une croyance répandue, il n'y a aucun besoin que cette vitesse soit verticale : la vitesse de libération est une quantité scalaire et non pas vectorielle. Il s'agit en fait d'une énergie cinétique de libération, mais comme celle-ci est proportionnelle à la masse de l'objet, il est commode de la caractériser par la vitesse qui lui est associée. Peu importe la direction vers laquelle le corps se dirige, sous réserve tout de même que ce ne soit pas directement vers la planète !

On peut aussi parler de vitesse parabolique : c'est la valeur, exprimée en fonction d'une planète, de la vitesse qu'il faut donner à un objet pour que la trajectoire de cet objet soumis exclusivement à l'attraction de cette planète soit une parabole (qui pourrait être dégénérée).

Au-dessus de cette vitesse, l'objet va quitter l'orbite de la planète et s'éloigner. En dessous, l'objet reste lié à la planète; il se mettra donc en orbite elliptique, et reviendra ou non s'écraser sur la planète en fonction des caractéristiques de cette orbite : dans ce cas, la direction joue un rôle aussi bien que le point de départ et la vitesse.

Notes et références de l'article

Voir aussi

Article connexe

• les Vitesses cosmiques, dont la Vitesse de satellisation minimale
• Delta v

• Portail de l’astronautique
• Portail de l’astronomie