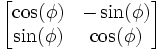SO(3)

SO(3)

Groupe orthogonal

Généralités

Soit E un espace vectoriel de dimension finie n sur un corps 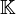\mathbb K, muni d'une forme quadratique q. Un automorphisme orthogonal pour cette forme quadratique est un automorphisme linéaire f du 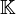\mathbb K-espace vectoriel E laissant invariant q. Autrement dit, pour tout vecteur x de E, on a : q(f(x)) = q(x).

Le groupe orthogonal est compact, en effet on est en dimension finie et il est borné car tous les endomorphismes orthogonaux sont unitaires et fermé car c'est l'image réciproque du singleton identité par l'application M \mapsto {}^tMM continue.

L'identité est un automorphisme orthogonal. L'ensemble des automorphismes orthogonaux est stable par composition et inversion. C'est donc un sous-groupe du groupe des automorphismes de E ; on l'appelle le groupe orthogonal associé à la forme quadratique q. Il est noté O(E,q).

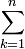Pour E={\mathbb K}^n, lorsque la forme quadratique q s'écrit : q(x) = \sum_{k=1}^n xk2, on appelle matrices orthogonales les matrices des automorphismes orthogonaux. Une matrice M est donc orthogonale si et seulement si tMM = In, où tM est la matrice transposée de M. Par définition, le groupe orthogonal de degré n du corps 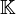\mathbb K est le groupe des matrices orthogonales n × n à coefficients dans 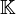\mathbb K, muni de la multiplication matricielle. 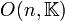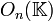Il est habituellement noté O(n,\mathbb K) ou O_n(\mathbb K). 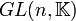C'est un sous-groupe du groupe général linéaire GL(n,\mathbb K).

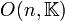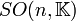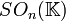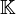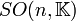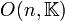Toute matrice orthogonale a un déterminant égal à 1 ou -1. Les matrices orthogonales n × n de déterminant 1 forment un sous-groupe invariant de O(n,\mathbb K) appelé le groupe spécial orthogonal et noté SO(n,\mathbb K) ou SO_n(\mathbb K). Si la caractéristique de \mathbb K est 2, alors les groupes orthogonal et spécial orthogonal coïncident. 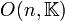Dans le cas contraire, l’indice de SO(n,\mathbb K) dans O(n,\mathbb K) est 2.

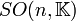O(n,\mathbb K) et SO(n,\mathbb K) sont des groupes algébriques, car la condition que leurs matrices soient orthogonales, c’est-à-dire que leur transposée soit leur inverse, peut s’exprimer comme un ensemble d’équations polynomiales dans les éléments de ces matrices.

Nombres réels

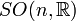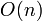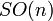Sur le corps \R des nombres réels, O(n,\R) et SO(n,\R) sont généralement simplement notés O(n)\,\! et SO(n)\,\! quand aucune confusion n’est possible. Ils forment deux groupes de Lie compacts de dimension 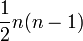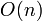{1\over 2}n(n-1). O(n)\,\! possède deux composantes connexes, 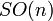SO(n)\,\! étant celle contenant la matrice identité.

Géométriquement, 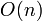O(n)\,\! est isomorphe au groupe des isométries de 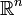\R^n laissant invariant l’origine. 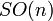SO(n)\,\! est isomorphe au groupe des isométries directes, ou rotations de 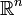\R^n laissant l’origine invariante.

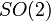SO(2)\,\! est isomorphe (en tant que groupe de Lie) au cercle S1, formé des nombres complexes de module 1, muni de la multiplication. Cet isomorphisme lie le nombre complexe 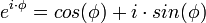e^{i\cdot \phi} = cos(\phi) + i\cdot sin(\phi) à la matrice orthogonale

\begin{bmatrix}\cos(\phi)&-\sin(\phi)\\ \sin(\phi)&\cos(\phi)\end{bmatrix}

Le groupe SO(3)\,\!, compris comme l’ensemble des rotations dans l’espace tridimensionnel, est appelé groupe des rotations.

En termes de topologie algébrique, pour n > 2, le groupe fondamental de 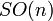SO(n)\,\! est le groupe cyclique d’ordre 2 et le groupe Spin Spin(n) est son revêtement universel. Pour n=2, le groupe fondamental est le groupe cyclique infini et son revêtement universel correspond à la droite des réels.

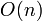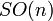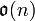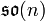L’algèbre de Lie associée aux groupes de Lie O(n)\,\! et SO(n)\,\! est formée des matrices n×n antisymétriques. Elle est généralement notée \mathfrak o(n)\,\! ou \mathfrak{so}(n)\,\!.

Nombres complexes

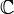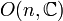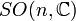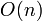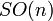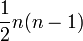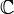Sur le corps \mathbb C des nombres complexes, O(n,\mathbb C) et SO(n,\mathbb C) (là aussi notés O(n)\,\! et SO(n)\,\! quand aucune confusion n’est possible) sont des groupes de Lie complexes de dimension {1\over 2}n(n-1) sur \mathbb C (le double sur 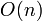\R). O(n)\,\! possède deux composantes connexes, 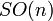SO(n)\,\! étant celle contenant la matrice identité. Pour 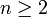n\ge 2, ces groupes ne sont pas compacts.

Pour n > 2, le groupe fondamental de 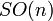SO(n)\,\! est le groupe cyclique d’ordre 2, tandis que le groupe fondamental de 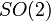SO(2)\,\! est le groupe cyclique infini.

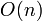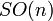L’algèbre de Lie associée aux groupes de Lie O(n)\,\! et SO(n)\,\! est formée des matrices complexes n×n antisymétriques.

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Groupe orthogonal ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article SO(3) de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”