Résonance paramagnétique électronique

Pour les articles homonymes, voir ESR.

Spectromètre à résonance paramagnétique électronique.

La résonance paramagnétique électronique (RPE) est une technique de mesure physique locale permettant d'obtenir des informations concernant la nature des espèces magnétiques en présence, ainsi que des informations sur leurs concentrations et les interactions magnétiques entre elles.

Son principe est analogue à celui de la résonance magnétique nucléaire (RMN), à la différence près qu'en RPE, ce sont les spins des électrons qui sont excités plutôt que les spins des noyaux atomiques.

Il est préférable de désigner cette technique par l'expression résonance de spin électronique (RSE) (ESR en anglais pour electron spin resonance), car les interactions entre les spins en présence ne se limitent pas nécessairement à des interactions paramagnétiques, mais peuvent être, surtout dans des composés magnétiquement concentrés, ferromagnétiques, ferrimagnétiques ou antiferromagnétiques. Cela dit, la plupart des applications utilisant cette technique concerne des espèces paramagnétiques, d'où l'usage de « RPE » plus fréquent que celui de « RSE ».

Historique

Cette technique a été découverte en 1944 par le physicien soviétique Yevgeny Zavoisky de l'université d'État de Kazan. La technique de la RSE en onde continue a longtemps été la méthode la plus utilisée. Dans celle-ci, le système est irradié en continue par un rayonnement micro-onde à une fréquence donnée. La RSE impulsionnelle est de plus en plus utilisée, notamment en biologie structurale où elle permet de connaître les distances entre radicaux, en matériaux pour connaître la structure locale autour de défaut paramagnétiques.

Principe

Séparation des niveaux d'énergie (pour le cas d'un spin S = 1/2) en présence d'un champ magnétique externe.

La résonance de spin électronique (RSE) est une méthode de spectroscopie sous champ magnétique. Grâce à sa spécificité et sa grande sensibilité, elle permet une détection directe des espèces paramagnétiques (radicaux, éléments de transition, défauts de structure…) caractérisées par la présence d'un ou plusieurs électron non apparié(s) (appelé aussi « électron célibataire ») sur la couche de valence. Le cas usuel où plusieurs électrons non appariés (S > 1/2) interviennent est celui des éléments de transitions.

Le principe de la RSE repose sur l'effet Zeeman : soumis à l'action d'un champ magnétique extérieur intense H, les niveaux d'énergie d'un spin S se séparent en (2S + 1) états, chacun affecté d'un nombre quantique m_S (m_S = -S, -S+1, -S+2, ..., S).

Ainsi, pour le cas d'un ion paramagnétique ne présentant qu'un seul électron célibataire (donc pour lequel S = 1/2), la présence du champ magnétique extérieur donne lieu à (2S + 1) = 2 états, correspondant à m_S = -1/2 et m_S = +1/2. L'énergie magnétique associée à chacun de ces états est donnée par m_Sgμ_BH, où g est le facteur de Landé lorsqu'il s'agit d'un électron libre, et vaut g_e = 2. Dans le cas général, le facteur g est différent de 2, et μ_B (qui est parfois noté β) est le magnéton de Bohr. Puis, sous l'action d'un second champ magnétique (champ hyperfréquence ou micro-onde) perpendiculaire au premier et d'amplitude beaucoup plus faible, ayant une fréquence ν, un photon d'énergie hν peut être absorbé (ou émis) si la séparation énergétique entre les 2 niveaux concernés, c'est-à-dire gμ_BH, se trouve égale à hν. C'est à cette valeur particulière de H que le phénomène de résonance se produit. Ainsi, la condition de résonance se résume par :

avec

• g = facteur de Landé (dans le cas d'un électron libre) ou facteur g en général ;
• μ_B (ou β) = magnéton de Bohr (μ_B = 9.2741 x 10^-24 J.T^-1) ;
• H = valeur du champ magnétique à la condition de résonance ;
• h = constante de Planck (h = 6.6261 x 10^-34 J.s) ;
• ν = fréquence du champ micro-onde ;
• E _f = énergie de l'état final ;
• E _i = énergie de l'état initial.

D'une façon plus générale, lorsqu'il y a plus que 2 états, les transitions permises sont celles pour lesquelles les états (initial et final) satisfont aux conditions ΔS = 0 et Δm_S = ± 1. Les autres transitions sont généralement interdites, sauf s'il y a un mélange entre les états quantiques.

La condition de résonance exprimée ci-dessus (Éq. 1) peut également s'écrire :

où γ désigne le rapport gyromagnétique.

Spectres typiques d'absorption (courbe du haut) et de la dérivée première de l'absorption (courbe du bas) obtenus à fréquence fixe et en faisant varier le champ magnétique statique externe.

L'équation (Éq. 2) montre qu'il existe une multitude de combinaisons possibles des valeurs de ν et H pour que la résonance ait lieu. En fait, un spectre de résonance de spin électronique peut théoriquement s'obtenir, soit en fixant le champ magnétique statique H et en faisant varier la fréquence ν du champ micro-onde, soit en faisant l'inverse. Cependant, en pratique, la plupart des spectromètres fonctionnent en permettant la variation du champ magnétique H alors que la fréquence ν est fixée.

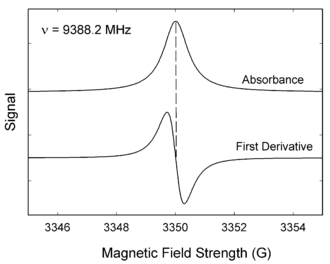
La figure ci-contre montre, dans sa partie supérieure, la variation de l'absorption, A, en fonction du champ magnétique statique H, lorsque la fréquence fixe utilisée est de 9388,2 MHz. La courbe inférieure représente la dérivée première de l'absorption par rapport au champ magnétique, dA/dH. La plupart des spectromètres de RSE utilisent un détection synchrone, c'est-à-dire que le champ magnétique est modulé autour d'une valeur centrale telle que

Le signal d'absorption peut s'écrire à l'ordre 1 sous la forme :

En filtrant la fréquence correspondant à ω on obtient dA/dH, la courbe dérivée.

Chaque signal ainsi enregistré est caractéristique de l'élément magnétique en présence et des interactions que cet élément ressent. Ces informations s'obtiennent à partir de (i) la valeur du champ de résonance (qui informe sur le facteur g de l'ion magnétique en question), (ii) l'aire en dessous de la courbe d'absorption (qui informe, entre autres, sur le nombre de spins présents) et (iii) la mi-largeur à mi-hauteur de la courbe d'absorption (qui informe sur les interactions ressenties par les spins). Le nombre de signaux indique parfois le nombre de site ou bien des interactions avec un (ou plusieurs) spins nucléaires. Si tel est le cas, on peut réaliser alors un spectre de résonance magnétique nucléaire détectée par RSE, l'ENDOR.

Théorie plus avancée

L'hamiltonien d'un électron de spin couplé à un champ magnétique , entouré de noyaux à spin non nuls , dans le cas général est donné par ^[1]:

Cette formule définit la représentation mathématique d'un électron dans un champ magnétique qui est couplé avec n noyaux. Ces mêmes noyaux subissent le champs magnétique mais également un terme dit quadrupolaire, un terme dipolaire. Les matrices d'interaction sont notées avec un chapeau. Souvent, elles sont appelées tenseurs à tort car elles n'en n'ont pas les propriétés.

1. , ce terme est l'effet de Zeeman. Dans le facteur , est contenue toute l'information sur la composition de l'orbitale dans laquelle se situe l'électron ;
2. , le terme de Zero field Splitting (ZFS), terme n'existant que pour S > 1 / 2, il représente les effets de couplage d'un spin sur lui-même, en général pénible à traiter... Mais plrésent par exemple pour le Cr3+, où le Fe3+ dans certaines matrices.
3. , ce terme est appelé couplage hyperfin, il représente le couplage de l'électron avec les noyaux à spin non nuls qui l'entourent : d'où la somme sur k ;
4. , terme dit de couplage quadrupolaire. Ce n'est qu'un effet ressentit par les noyaux, et il n'existe que si le noyaux est à spin I>1/2. Dans ce terme est contenu le gradient de champ électrique reseentit pas le noyaux. Ainsi si le gradient de champ se modifie sous l'effet d'un dopant plus qu'un autre, cela peut être en accord avec la modification de la fonction d'onde localement.
5. , couplage dipolaire entre deux noyaux i et k, toujours présent.
6. , terme Zeeman nucléaire, c'est l'effet du couplage entre un noyau et un champ magnétique.

Bien sûr l'effet de ces termes n'est pas résolu, c'est-à-dire n'est pas visible, sur la plupart des spectres RPE. Souvent, on a recours à des approximations, comme la théorie des perturbations au premier et deuxième ordre. Souvent cette analyse suffit, sinon il faut diagonaliser l'hamiltonien, c'est-à-dire trouver ces valeurs propres, qui donneront les fréquences de transition entre les états. Néanmoins, l'effet de chacun de ces termes peut être étudié avec l'ENDOR, la RPE impulsionnelle et l'ENDOR impulsionnelle. Pour l'étude de systèmes complexes, la combinaison de ces techniques est souvent nécessaire pour déterminer toutes les matrices.

Appliqué à l'exemple précédent, l'hamiltonien d'un spin électronique S = 1 / 2 serait simplement

après diagonalisation, en supposant le champ magnétique orienté suivant z, on aurait

.

Si le spin est de 1/2, m_s ne prends que deux valeurs 1/2 et -1/2, et la transtion à lieu entre ces deux états.

Applications

Analyse des matériaux

La RSE est utile pour l'étude de la structure locale de l'ensemble des matériaux pouvant présenter en leur sein un élément paramagnétique, utile pour pouvoir décrire l'environnement local. Elle peut servir à l'étude, par exemple, de défauts créés par le passage d'un rayonnement (α, β, γ, particules chargées...), donnant ainsi une mesure absolue de leur concentration dans la structure (à condition d'avoir un étalon). On peut étudier des ions paramagnétiques dans les structures de complexes dans les composés organiques ou de minéraux. De nombreux objets peuvent ainsi être étudiés grâce à cette technique, allant des matériaux désordonnés (verres) à des structures cristallines (minéraux) en passant par des matériaux organiques.

L'exploitation des spectres RSE passe parfois par une étape de simulation afin de pouvoir en déduire les différentes informations concernant l'environnement des éléments paramagnétiques présents et de suivre l'évolution du système en fonction des conditions expérimentales et de mesure.

Datation archéologique

La RSE est également utilisée dans le cadre de datations en archéologie préhistorique. Elle s'applique en particulier à l'émail dentaire de grands mammifères fossiles, à des grains de quartz extraits de sédiments archéologiques ou à des carbonates (stalagmites, coraux, etc.). Son champ d'application est très étendu, d'environ 20 000 ans à un million d'années.

Autres

La RSE s'applique aussi aux modèles biologiques.

La RPE s'est avérée une technique de choix pour déterminer les paramètres associés à la fluidité membranaire.

La RPE a été utilisée pour mesurer la quantité d'énergie appliquée à l'échelle moléculaire lors de réactions mécanochimiques (M. Baron & al.).

Notes et références

Articles connexes

• Paramagnétisme
• Électron
• Résonance
• Spin
• Physique des particules
• Atome
• interaction rayonnement-matière
• Biophysique

Bibliographie

• A. Abragam et B. Bleaney, Electron Paramagnetic Resonance of Transition Ions, Oxford University Press, 1970, ISBN 0-486-65106-1
• A. Schweiger et G. Jeschke, Principles of pulse electron paramagnetic resonance. Oxford University Press, 2001, USA.
• M. Baron, A. Chamayou, L. Marchioro, J. Raffi. (2005). "Radicalar probes to measure the action of energy on granular materials". Adv. Powder Technol 16 (3): 199–212. doi:10.1163/1568552053750242.

Liens et documents externes

• Spectrométrie de résonance paramagnétique électronique - RPE [PDF]

• Portail de l’archéologie
• Portail de la physique
• Portail de la chimie