Relation de Varignon

Relation de Varignon

Théorème de Varignon

Il existe deux théorèmes démontrés par Pierre Varignon.

Théorème mathématique

Soit ABCD un quadrilatère quelconque et I, J, K et L les milieux de ses côtés. IJKL est un parallélogramme.

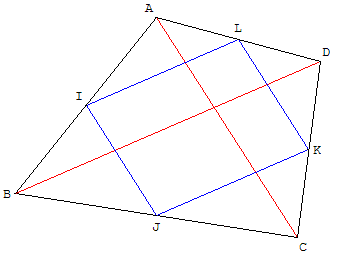
Varignon.gif

D'autre part, si ABCD est plan et convexe, son aire est le double de celle de IJKL.

En corollaire les médianes d'un quadrilatère ont même milieu (étant les diagonales du parallélogramme),

le périmètre du parallélogramme de Varignon est égal à la somme des longueurs des diagonales du quadrilatère.

Démonstration

Par application du théorème des milieux, on montre que les côtés opposés de IJKL sont chacun parallèle à une diagonale de ABCD, donc parallèles entre eux.

D'après le théorème de Thalès, la base b de IJKL est égale à la moitié de la diagonale d de ABCD, et la hauteur h est égale à la moitié de la hauteur h’ prise d'un sommet à l'autre de ABCD (perpendiculairement à la diagonale).

Donc Aire(ABCD) = \frac 12 × d × h’ = \frac 12 × 2b × 2h = 2 × Aire(IJKL).

Théorème mécanique

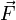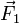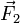Une force \vec{F} se décompose en deux forces \vec{F}_1 et \vec{F}_2 :

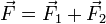\vec{F} = \vec{F}_1 + \vec{F}_2.

Le théorème de Varignon énonce que

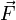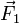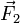le moment de la force \vec{F} par rapport à un point est égal à la somme des moments de forces \vec{F}_1 et \vec{F}_2 par rapport à ce même point,

si l'on considère un point A quelconque :

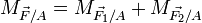M_{\vec{F}/A} = M_{\vec{F_1}/A} + M_{\vec{F_2}/A} (en valeur algébrique),

ou bien

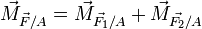\vec{M}_{\vec{F}/A} = \vec{M}_{\vec{F_1}/A} + \vec{M}_{\vec{F_2}/A} (en vectoriel)


  • Portail de la géométrie Portail de la géométrie
Ce document provient de « Th%C3%A9or%C3%A8me de Varignon#Th.C3.A9or.C3.A8me m.C3.A9canique ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Relation de Varignon de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Mecanique du solide — Mécanique du solide Illustration de la complexité du solide par rapport au point matériel La mécanique du solide est la partie de la mécanique qui s intéresse aux objets que l on ne peut réduire en un point matériel. Cela permet notamment de… …   Wikipédia en Français

  • Mécanique Du Solide — Illustration de la complexité du solide par rapport au point matériel La mécanique du solide est la partie de la mécanique qui s intéresse aux objets que l on ne peut réduire en un point matériel. Cela permet notamment de décrire et modéliser les …   Wikipédia en Français

  • Mécanique des solides — Mécanique du solide Illustration de la complexité du solide par rapport au point matériel La mécanique du solide est la partie de la mécanique qui s intéresse aux objets que l on ne peut réduire en un point matériel. Cela permet notamment de… …   Wikipédia en Français

  • Mécanique du solide — Illustration de la complexité du solide par rapport au point matériel La mécanique du solide est la partie de la mécanique qui s intéresse aux objets que l on ne peut réduire en un point matériel. Cela permet notamment de décrire et modéliser les …   Wikipédia en Français

  • Statique du solide — Pour les articles homonymes, voir Statique. La statique du solide est la branche de la statique étudiant l équilibre des pièces dans un mécanisme. C est un maillon essentiel dans le dimensionnement des systèmes mécaniques réels. Sommaire 1… …   Wikipédia en Français

  • Vitesse angulaire — Pour les articles homonymes, voir pulsation (homonymie). En physique, et plus spécifiquement en mécanique, la vitesse angulaire ω, aussi appelée fréquence angulaire ou pulsation, est une mesure de la vitesse de rotation. Elle s exprime dans le… …   Wikipédia en Français

  • Torseur — Un torseur est un outil mathématique utilisé principalement en mécanique du solide indéformable, pour décrire les mouvements des solides et les actions mécaniques qu ils subissent de la part d un environnement extérieur. Sommaire 1 Définition 2… …   Wikipédia en Français

  • Produit vectoriel — En mathématiques, et plus précisément en géométrie, le produit vectoriel est une opération vectorielle effectuée dans les espaces euclidiens orientés de dimension trois[1],[2]. Le formalisme utilisé actuellement est apparu en 1881 dans un manuel… …   Wikipédia en Français

  • Double produit vectoriel — Produit vectoriel Le produit vectoriel est une opération vectorielle effectuée dans les espaces euclidiens orientés de dimension trois[1]. Le formalisme utilisé actuellement est apparu en 1881 dans un manuel d analyse vectorielle écrit par Josiah …   Wikipédia en Français

  • Produit vectoriel et algèbre — Produit vectoriel Le produit vectoriel est une opération vectorielle effectuée dans les espaces euclidiens orientés de dimension trois[1]. Le formalisme utilisé actuellement est apparu en 1881 dans un manuel d analyse vectorielle écrit par Josiah …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”