Rapport Homothétique

Une homothétie est une transformation géométrique d'un espace affine dans lui-même, fixant un point O appelé centre de l'homothétie. Une homothétie se définit par son centre (un point de l'espace affine) et son rapport (un scalaire non nul). La composée de deux homothéties est soit une translation si le produit des rapports vaut 1, soit une nouvelle homothétie. L'ensemble des homothéties et des translations est stable par composition. Les symétries centrales sont des exemples d'homothéties, dont le rapport vaut -1. (homothétie: du grec homos = semblable et thetis = action de poser)

Les homothéties préservent l'alignement des points et les rapports algébriques. Elles transforment une droite en une droite qui lui est parallèle. En géométrie euclidienne, elles apparaissent comme des cas particulier des similitudes ; les homothéties préservent les angles et dilatent les distances.

La transformation d'une droite en une droite parallèle est liée au théorème de Thalès. Dans une approche axiomatique de la géométrie, les homothéties ne peuvent pas se définir en l'absence de l'axiome de Désargues.

Sommaire 1 Définition en géométrie affine 1.1 Propriétés affines 1.2 Théorème de Thalès 1.3 Composition 2 Propriété en géométrie euclidienne 3 Historique 4 Approche axiomatique 5 Géométrie vectorielle

Définition en géométrie affine

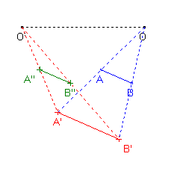
Dans un espace affine P, pour un point donné O de P et un scalaire non nul k, l'homothétie de centre O et de rapport k est une transformation f du plan P qui laisse le point O invariant et telle que, pour tout point M distinct de O :

• Les points O, M et f(M) sont alignés ;
• Le rapport algébrique vaut k :

.

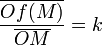Deux cas particuliers (distincts en caractéristique différente de 2) doivent être mentionnés :

• Si k = 1, chaque point étant invariant, l'homothétie est la transformation identique.
• Si k = − 1, l'homothétie de rapport -1 est la symétrie centrale de centre O.

Propriétés affines

• Toute homothétie transforme une droite en une droite qui lui est parallèle.

Sans utiliser le théorème de Thalès, si h est une homothétie de centre O envoyant les points M et N sur f(M) et f(N), alors la relation de Chasles donne :

f(M)f(N) = Of(N) − Of(M) = k.(ON − OM) = k.MN.

En particulier, les droites (f(M)f(N)) et (MN) ont même droite vectorielle directrice ; elles sont donc parallèles.

• Toute homothétie préserve le parallélisme : deux droites parallèles sont envoyées sur deux droites parallèles.

En effet, si deux droites d et d' sont parallèles, et que h est une homothétie, alors par la propriété précédente, h(d) et d sont parallèles, et h(d') et d' sont aussi parallèles. Par transitivité, les droites h(d) et h(d') sont donc parallèles.

• Toute homothétie préserve les rapports algébriques.

Si M, N, P et Q sont quatre points alignés, et que h est une homothétie de rapport k, il a été obtenu :

h(M)h(N) = k.MN et h(P)h(Q) = k.PQ.

Si PQ = u.MN, alors, comme k est non nul, h(P)h(Q) = u.h(M)h(N). Donc, h préserve les rapports algébriques.

Théorème de Thalès

Les propriétés citées ci-dessus sont une reformulation du théorème de Thalès :

Théorème de Thalès :^{[réf. nécessaire]} Soient un triangle OMB et deux points N et A respectivement sur les droites (OM) et (0B). Alors les droites (BM) et (AN) sont parallèles ssi les rapports algébriques suivants sont égaux :

.

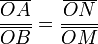En reprenant les notations du théorème cité, si les points A et N sont les images respectives des points B et M par la même homothétie de centre O, l'égalité des rapports algébriques est vérifiée. Le sens réciproque implique que les droites (AN) et (BM) sont parallèles. Le théorème de Thalès montre que toute homothétie transforme une droite en une droite qui lui est parallèle.

Par ailleurs, le théorème de Thalès montre qu'il existe exactement une unique homothétie de centre O envoyant M sur N. Cette homothétie envoie tout point B non aligné avec O, M et N sur le point d'intersection de la droite (0B) avec la parallèle à (BM) passant par N. La construction de l'image d'un point de la droite (0M) nécessite de construire au préalable l'image d'un point non aligné avec O, M et N.

Composition

La composée de deux homothéties de centre O et de rapports k et k' est une homothétie de centre O et de rapport kk'. L'ensemble des homothéties de centre O est donc stable par composition : il forme un sous-groupe commutatif du groupe des transformations de l'espace.

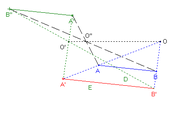
La composée de deux homothéties de centres différents O et O' et de rapports k et k' est :

• une translation de vecteur 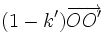si le produit kk' =1 ;
• une homothétie de rapport kk' et de centre O" barycentre des points (O, kk'- k') et (O', k'-1) si kk' est différent de 1.

La composée t o h d'une homothétie de centre O et de rapport k et d'une translation de vecteur est aussi une homothétie de rapport k et de centre O" barycentre des points (O, k) et (O', -1) où O' est le point tel que 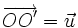. Enfin la composée h o t est une homothétie de rapport k et de centre O" barycentre de (O', k) et (O, -1) où O' est le point tel que .

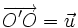Ces propriétés montrent que l'ensemble des homothéties et des translations est stable par composition ; il forme un sous-groupe non commutatif du groupe des transformations de l'espace.

Propriété en géométrie euclidienne

En géométrie euclidienne, la composée d'une rotation de centre O et d'une homothétie de centre O s'appelle une similitude de centre O. Comme toutes les similitudes, les homothéties vérifient les propriétés suivantes :

• Toute homothétie préserve les angles, et donc en particulier l'orthogonalité. Une homothétie est donc une transformation conforme.
• Une homothétie transforme un cercle en un cercle.
• Une homothétie de rapport k modifie les distances par un facteur | k | et modifie les volumes par un facteur | k | ⁿ où n est la dimension de l'espace.

Historique

Le terme, dû au mathématicien français Michel Chasles, est composé des deux éléments d'origine grecque, le préfixe homo- pour « semblable » et thesis pour « position ». Il traduit la correspondance entre deux figures de même forme et de même orientation. Ainsi, deux poupées russes regardant dans la même direction peuvent être vues comme homothétiques.

Dans la suite nous traitons des homothéties du plan, mais les propriétés énoncées restent vraies dans l'espace.

Approche axiomatique

Si ABCD est un trapèze tel que 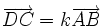avec k différent de 1, il existe deux homothéties transformant [AB] en [CD]. Une de centre O' intersection des diagonales et de rapport -k et l'autre, de centre O intersection des droites (AD) et (BC) et de rapport k.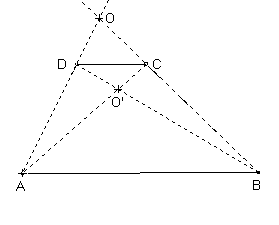

Géométrie vectorielle

Dans un espace vectoriel V sur un corps K, on appelle homothétie de rapport k (k non nul), l'application qui, à tout vecteur , associe le vecteur k.

C'est un cas particulier d'application linéaire. Dans une homothétie, il n'existe qu'une seule valeur propre : k et tous les vecteurs sont des vecteurs propres. La matrice d'une homothétie dans un espace vectoriel de dimension n est k*I_n où I_n est la matrice Identité.

• Portail de la géométrie