Homothetie (mathematiques elementaires)

Homothetie (mathematiques elementaires)

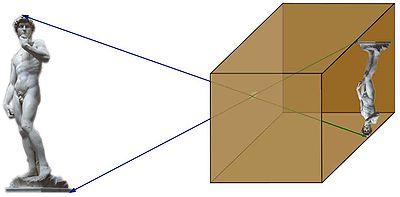
Homothétie (mathématiques élémentaires)

Fig. 1. L'image par une chambre noire correspond à une homothétie de centre la lentille et de rapport négatif.

Dans la « vie courante », l'homothétie correspond aux agrandissements et aux réductions.

Définition

Soit un point M,un point O et un nombre k.

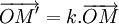
On dit que le point M' est l' homothétie de M par l' homothétie de centre O et de rapport k(ou h(o,k)) si, et seulement si, \overrightarrow{OM'}=k.\overrightarrow{OM}\,

Construction de l'homothétique d'un point

  • Tracer la droite (OM).
  • Si k est positif, placer sur (OM) le point M' tel que le sens de O vers M soit le même que celui de O vers M' .
  • Si k est négatif, placer sur (OM) le point M' tel que le sens de M vers O soit le même que celui de O vers M' .
  • Alors M' est l'homothétique de M.

Propriétés

Propriété 1 : L'homothétique d'une droite d est une droite d' qui est parallèle à d.Celui d'un segment [AB] est un segment [ A'B' ] tel que AB = |k| A'B' .

Propriété 2 : L'homothétique d'un cercle C de centre A et de rayon r est un cercle C' de centre A' , l'homothétique de O, et de rayon r' =|k|r.

Propriété 3 dite "de conservation" : L'homothétie conserve :

  • les angles(l'homothétique d'un angle est un angle de même mesure);
  • les parallèles (les homothétiques de deux droites parallèles sont parallèles);
  • les rapports de longueurs (cf.le Théorème de Thalès).

Propriété 4: Une homothétie de rapport :

  • k>1 est un agrandissement de rapport k;
  • k<1 est une réduction de rapport {1\over k}.
  • Portail de la géométrie Portail de la géométrie
Ce document provient de « Homoth%C3%A9tie (math%C3%A9matiques %C3%A9l%C3%A9mentaires) ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Homothetie (mathematiques elementaires) de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

  • Homothétie (mathématiques élémentaires) — Dans la « vie courante », l homothétie correspond aux agrandissements et aux réductions. Article détaillé : homothétie. Définition Soit un point M,un point O et un nombre k. On dit que le point M est l image du point M par l… …   Wikipédia en Français

  • Mathématiques élémentaires — Les mathématiques élémentaires[1] regroupent des notions et techniques mathématiques abordées dans l enseignement scolaire primaire et secondaire. Elles se démarquent ainsi des mathématiques de l enseignement supérieur et notamment, en France,… …   Wikipédia en Français

  • Probabilités (mathématiques élémentaires) — Pour les articles homonymes, voir Interconnexions entre la théorie des probabilités et les statistiques. Les probabilités sont nées du désir de prévoir l imprévisible ou de quantifier l incertain. Mais il faut avant tout préciser ce qu elles ne… …   Wikipédia en Français

  • Fonction (mathématiques élémentaires) — Pour les articles homonymes, voir Fonction. En mathématiques élémentaires, la plupart des fonctions rencontrées sont des fonctions numériques, mais la notion de fonction ne se limite pas à celle ci. L article qui suit présente quelques règles à… …   Wikipédia en Français

  • Statistiques (mathématiques élémentaires) — Une enquête statistique consiste à observer une certaine population (élèves d’une classe, personnes âgées de 20 à 60 ans dans une région donnée, familles dans une région donnée, exploitations agricoles, appartements, travailleurs…) et à… …   Wikipédia en Français

  • Limite (mathématiques élémentaires) — Pour les articles homonymes, voir Limite. La notion de limite est très intuitive malgré sa formulation abstraite. Pour les mathématiques élémentaires, il convient de distinguer une limite en un point réel fini (pour une fonction numérique) et une …   Wikipédia en Français

  • Logique (mathématiques élémentaires) — La logique est le lieu où le langage puis les axiomes (logiques ou propres à certaines théories) des mathématiques sont définis ce qui est à la base des démonstrations en mathématique. Bien qu elle apparaisse de manière cachée dans toute l… …   Wikipédia en Français

  • Suite (mathématiques élémentaires) — Intuitivement une suite réelle est une règle qui associe à chaque entier naturel n un certain nombre réel ; on dit alors que ce nombre réel est indexé par l’entier. En fait une suite est un moyen d’indexer des nombres réels par des entiers… …   Wikipédia en Français

  • Distributivité (mathématiques élémentaires) — La distributivité est une propriété de la multiplication qui permet d effectuer de deux manières différentes le produit d un nombre par une somme : Ici on a distribué a à chaque terme de la somme Ici on a distribué c à chaque terme de la… …   Wikipédia en Français

  • Démonstration (mathématiques élémentaires) — Démontrer une propriété c est utiliser des théorèmes, des définitions ou des axiomes que l on sait être vrais et quelques règles de logique élémentaire. Elle expose une justification d’une propriété nouvelle algébrique, géométrique, numérique…… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”