Cercle de Tucker

Définition des cercles de Tücker

Sommaire 1 Définition 1 : homothétie 2 Définition 2 : Construction d'une antiparallèle 3 Triangle tangentiel à UVW 4 Définition 3 : Construction de trois antiparallèles de longueur égale 5 Milieu des cordes, construction à partir d'un centre donné 6 Deux cercles de Tücker

Définition 1 : homothétie

Dans une homothétie de centre L, le point de Lemoine, de rapport k (k ≠ 1 et k ≠ 0), le triangle ABC a pour image A’B’C’. Les côtés du triangle A’B’C’ rencontrent ceux de ABC en six points. Ces points sont cocycliques et sont situés sur un cercle (T) dit de Tücker du triangle ABC.

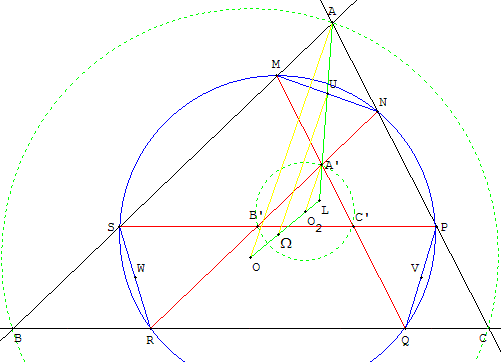
Propriétés
Les milieux U, V, W des segments [MN], [PQ], [RS] sont situés sur les symédianes et forment un triangle UVW homothétique de ABC dans une homothétie de centre L.

Les droites (MN), (PQ) et (RS) sont antiparallèles aux côtés du triangle et les segments qu'elles déterminent sont de même longueur.

Le centre Ω du cercle (T) est le milieu du segment [OO2] formé par les centres des cercles circonscrits aux triangles ABC et A’B’C’.

Indications
Les milieux U, V, W des segments [MN], [PQ], [RS] sont situés sur les symédianes, les segments sont antiparallèles aux cotés opposés.

Voir : milieu d'une antiparallèle

Les droites (MN, CB) sont antiparallèles aux droites (AB, CA) : (AB, MN) = (CB, CA).
Les droites (SR, CA) sont aussi antiparallèles aux droites (BC, BA) : (BA, SR) = (CA, CB).

On en déduit que (BA, SR) = - (AB, MN).
Comme (AB) //(NR) on a : (BA, SR) = - (NR, MN).
Avec les points de l'hexagone (SM, SR) = (NM, NR).
Les points S, M, N, R n'étant pas alignés, cette égalité d'angles montre qu'ils sont cocycliques, situés sur un cercle (T).

De (BC)//(PS) et (MN) antiparallèle à (BC) on en déduit que (PS) est antiparallèle à (MN) par rapport à (MS) et (PN). (PS, PN) = (MS, MN). P, S, M, N sont cocycliques, P appartient au cercle contenant S, M, N : le cercle (T). On montre de même que (T) contient (Q).

Démonstrations : Sortais Yvonne et René - La géométrie du triangle - Hermann 1997

Définition 2 : Construction d'une antiparallèle

ABC est un triangle de cercle circonscrit (Γ) de centre O.

À partir d'un point M de (AB) distinct de A mener la droite antiparallèle de (BC) par rapport à (AB, AC). C'est la parallèle à la tangente en A à (Γ), donc perpendiculaire à (AO). Elle coupe (AC) en N. La parallèle à (AB) passant par N coupe (BC) en R. Le cercle circonscrit au triangle MNR recoupe les côtés du triangle ABC en P, Q et S.

Nous obtenons une configuration de six points situés sur un cercle de Tücker.

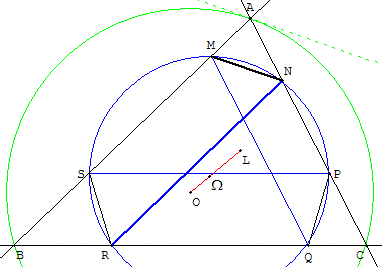
Propriétés
Les droites parallèles (AB) et (NR) coupent le cercle suivant deux cordes égales, d'où MN = SR.

(RS) antiparallèle à (AC) par rapport à (BA, BC) :

(RS, BA) = (RS, RN) car (BA)//(RN)
(RS, RN) = (MS, MN) = (AB, MN), angles inscrits de droites
(AB, MN) = (BC, AC) car les droites (MN), (BC) sont antiparallèles aux droites (AB), (AC).

On a donc (RS, BA) = (BC, AC) : les droites (RS), (AC) sont antiparallèles aux droites (BA), (BC).

(MQ) parallèle à (AC) :

(MQ, AC) = (MQ, MN) + (MN, AC)
(MQ, MN) = (RQ, RN) = (RQ, AB), angles inscrits de droites
(MN, AC) = (AB, BC) car les droites (MN), (BC) sont antiparallèles aux droites (AB), (AC)
(MQ, AC) = (RQ, AB) + (AB, BC) = (RQ, BC) = 0.

(MQ) // (AC). Ces parallèles coupent le cercle suivant deux cordes égales, d'où MN = PQ et MN = PQ = SR.

De l'égalité PQ = SR il résulte le parallélisme de (BC) et (SP).

Un calcul d'angles analogue au premier calcul permet de déduire que (PQ) est antiparallèle à (AC) par rapport à (BA, BC).

Conclusions

Les six points jouent des rôles analogues. Par chaque point on mène deux droites : l'une parallèle à la tangente à (Γ) en l'un des sommets du côté qui le porte, et l'autre parallèle à l'autre côté issu de ce sommet.

Par tout point d'un côté distinct des sommets passe deux cercles de Tücker obtenus en considérant les deux tangentes à (Γ) aux deux sommets des côtés qui le porte.

Voir : Quadrature n°63 Janvier-Mars 2007

Triangle tangentiel à UVW

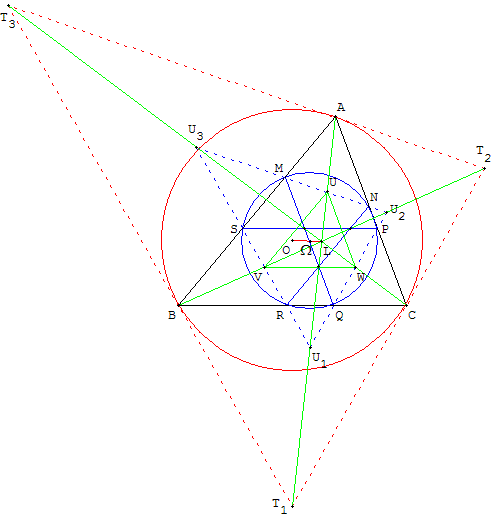
Les points U₁, U₂ et U₃, intersections des droites (PQ), (RS) et (MN), sont situés sur les symédianes.

Le triangle U₁U₂U₃ est le triangle tangentiel de UVW, Il est homothétique du triangle tangentiel T₁T₂T₃ de ABC dans l'homothétie de centre L.

Autre construction du cercle à partir de M et N

A partir d'un point M de (AB) distinct de A mener la parallèle à la tangente en A à (Γ). Elle coupe (AC) en N. Construire les points U₂ et U₃, intersection de (MN) avec les symédianes (CL) et (BL). Tracer les droites (RS) et (PQ) parallèles aux tangentes à (Γ) en B et C et trouver les quatre autres points du cercle.

Définition 3 : Construction de trois antiparallèles de longueur égale

Les droites (MN), (PQ) et (RS) sont antiparallèles aux côtés du triangle et les segments qu'elles déterminent sont de même longueur.

Cette propriété peut être prise comme définition en déterminant trois segments [MN], [PQ], [RS] de longueur égale et parallèles aux tangentes en A, B, C au cercle circonscrit.

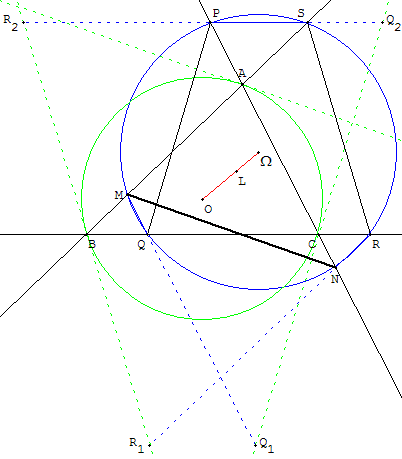
Construction

A partir d'un point M de (AB) distinct de A mener la parallèle à la tangente en A à (Γ), donc perpendiculaire à (AO). Elle coupe (AC) en N. Reporter la longueur MN sur la tangente en B à (Γ) en R₁ et R₂, sur la tangente en C en Q₁ et Q₂. La parallèle à (AB) passant par R1 coupe (BC) en R, la parallèle à (BC) passant par R2 coupe (AB) en S. La parallèle à (AC) passant par Q1 coupe (BC) en Q et la parallèle à (BC) passant par Q₂ coupe (AC) en P.

Nous obtenons une configuration de six points, ces points sont cocycliques et situés sur un cercle de Tücker.

Justification

La parallèle à (AB) passant par N coupe la tangente en B à (Γ) en R₁ et (BC) en R. Par parallélisme, le cercle circonscrit au triangle MNR recoupe les côtés du triangle ABC en P, Q et S. Comme on l'a vu dans la définition 2, c'est un cercle de Tücker.

[MN] étant construit, il peut être délicat de choisir, à partir de B, la direction vers R₁ ou R₂ pour placer R.

Milieu des cordes, construction à partir d'un centre donné

Les milieux forment un triangle UVW se déduisant de ABC dans une homothétie de centre L de rapport t avec |t| = LU/LA. Dans cette homothétie, le point O a pour image Ω avec LΩ/LO = |t|. Ce point Ω est le centre du cercle circonscrit à UVW. La droite (UΩ) parallèle à (OA) est perpendiculaire à (MN), c'est la médiatrice de [MN]. De même (VΩ) est la médiatrice de [PQ]. Ω est bien le centre du cercle (T).

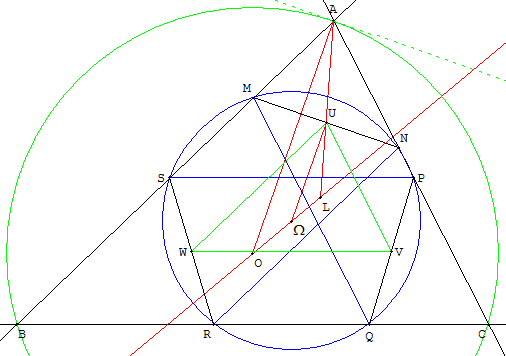
Un cercle de Tücker est caractérisé par son centre Ω situé sur (OL), distinct de O et de L.

Construction

La parallèle à (OA) passant par Ω coupe (LA) en U.

M et N sont situés sur la perpendiculaire en U à (OA) et on complète R par parallélisme pour construire le cercle circonscrit à MNR.

Deux cercles de Tücker

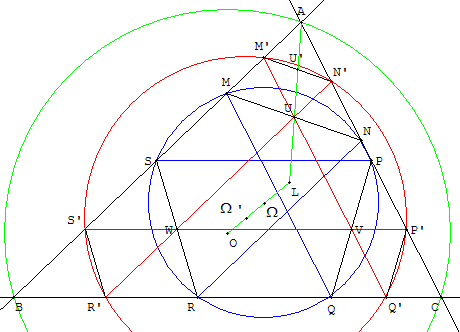
|t| = LU/LA.

En prolongeant les côtés du triangle U’V’W’ jusqu'à ceux du triangle ABC, nous obtenons un deuxième cercle de Tücker passant par M’N’P’Q’R’S’.

En prenant les milieux des cordes [M’N’], [P’Q’], [R’S’] , le triangle U’V’W’ est homothétique de ABC dans une homothétie de centre L de rapport t’ : |t’| = LU’/LA = |(t+1)/2| (en effet U’ est le milieu de [UA]).

• Portail de la géométrie