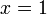- Quantificateur existentiel
-
Notation (mathématiques)
 Pour les articles homonymes, voir Notation.
Pour les articles homonymes, voir Notation.On utilise en mathématiques un ensemble de notations pour condenser et formaliser les énoncés et les démonstrations.
Quand deux traductions d'une notation sont données, l'une est la traduction mot-à-mot et l'autre est la traduction naturelle.
Sommaire
Introduction
Comme tous les autres langages formels, ces notations ont pour but de retirer l'ambiguïté d'une proposition en la décomposant en un ensemble limité de symboles dont l'agencement ne peut avoir qu'un unique sens.
Par exemple, pour dire que x vaut un, on utilisera :
Ce langage permet aussi dans une moindre mesure de faciliter la communication entre des mathématiciens ne parlant pas la même langue. S'il ne remplace pas complètement le langage naturel, il permet d'exprimer les concepts mathématiques les plus complexes sous une forme qui est identique suivant les langues et les cultures, évitant ainsi les quiproquos sur les concepts mathématiques, par des gens ne maîtrisant pas toutes les subtilités grammaticales et syntaxiques de la langue de communication employée.
Malheureusement, certains concepts du langage formel mathématique restent spécifiques à une culture donnée. Ainsi, dans la littérature mathématique francophone, l'assertion
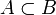 signifie « l'ensemble A est un sous-ensemble ou est égal à B » alors que dans la littérature mathématique anglophone, il signifiera plutôt « l'ensemble A est un sous-ensemble strict de B ».
signifie « l'ensemble A est un sous-ensemble ou est égal à B » alors que dans la littérature mathématique anglophone, il signifiera plutôt « l'ensemble A est un sous-ensemble strict de B ».La liste de symboles qui suit n'est pas exhaustive. Cependant, l'ensemble des symboles présentés ici sont utilisés de façon universelle dans la littérature mathématique francophone.
Opérateurs logiques
Voir algèbre de Boole pour plus de détails.
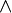 , et.
, et.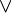 , ou.
, ou.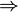 , implique.
, implique.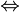 , équivaut à.
, équivaut à.
Ensembles
Ensembles usuels
 , ensemble des entiers naturels.
, ensemble des entiers naturels. , ensemble des entiers relatifs.
, ensemble des entiers relatifs.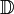 , ensemble des nombres décimaux.
, ensemble des nombres décimaux. , ensemble des rationnels.
, ensemble des rationnels. , ensemble des nombres réels.
, ensemble des nombres réels.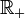 , ensemble des nombres réels positifs ou nuls.
, ensemble des nombres réels positifs ou nuls.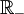 , ensemble des nombres réels négatifs ou nuls.
, ensemble des nombres réels négatifs ou nuls. , ensemble des nombres complexes.
, ensemble des nombres complexes.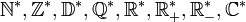 , les mêmes ensembles privés de zéro.
, les mêmes ensembles privés de zéro.
Relations sur les ensembles
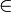 , appartenance.
, appartenance.
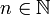
- n appartient à l'ensemble des entiers naturels.
- n est un entier naturel.
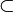 , inclusion.
, inclusion.
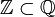
 est inclus dans
est inclus dans  .
.- Les entiers relatifs sont des rationnels.
Quantificateurs
Voir calcul des prédicats pour un point de vue plus théorique sur ces notations.
Pour tout
Notation
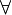 , pour tout, quel que soit.
, pour tout, quel que soit.Exemples
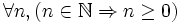
-
- Quel que soit n entier naturel, n est supérieur ou égal à zéro.
 est minoré par zéro.
est minoré par zéro.
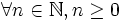
-
- Forme condensée.
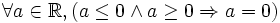
-
- Pour tout réel a, si a est inférieur ou égal à zéro, et si a est supérieur ou égal à zéro, alors a est nul.
- Tout réel, à la fois supérieur ou égal à zéro et inférieur ou égal à zéro, est nul.
Il existe
Notation
 , il existe (au moins un).
, il existe (au moins un).Exemples
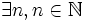
-
- Il existe un élément dans
 .
.  est non vide.
est non vide.
- Il existe un élément dans
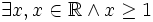
-
- Il existe un réel x tel que x soit plus grand ou égal à un.
 n'est pas majoré par 1.
n'est pas majoré par 1.
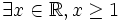
-
- Forme condensée.
Exemples généraux
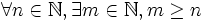
-
- Pour tout entier naturel n, il existe un autre entier naturel m tel que m soit supérieur ou égal à n.
- Tout entier naturel est inférieur ou égal à au moins un autre entier naturel.
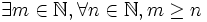
-
- Il existe un entier naturel m tel que quel que soit l'entier naturel n, m soit plus grand que n.
 est majoré.
est majoré.
- On notera donc que l'ordre des quantificateurs est important : la première proposition est vraie, l'autre est fausse.
![\forall (a,l)\in\mathbb{R}^2, \exists f : \mathbb{R} \rightarrow \mathbb{R}, \forall \epsilon \in \mathbb{R_+^*}, \exists \alpha\in\mathbb{R_+^*}, \forall x\in[a-\alpha,a+\alpha], |f(x)-l|\le\epsilon](/pictures/frwiki/98/bdc4ee9d572b4ded9f3a0d54c65a2882.png)
-
- Pour tout réels a et l, il existe une application f de
 dans
dans  telle que f tend vers l en a.
telle que f tend vers l en a.
- Pour tout réels a et l, il existe une application f de
- Les quantificateurs permettent de définir les notions mathématiques.
Il existe un unique
La notation
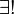 qui signifie il existe un unique.... Ce quantificateur se définit à partir des quantificateurs précédents et de l'égalité. Pour P(x) une propriété de x :
qui signifie il existe un unique.... Ce quantificateur se définit à partir des quantificateurs précédents et de l'égalité. Pour P(x) une propriété de x :- ∃! x P(x) équivaut par définition à ∃ x [P(x) ∧ ∀ y (P(y) ⇒ y = x)]
ou de façon équivalente :
- ∃! x P(x) équivaut à ∃ x P(x) ∧ ∀ x ∀ y [(P(x) ∧ P(y)) ⇒ y = x] .
Exemple.
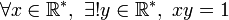 : pour tout x réel non nul, il existe un unique réel y non nul tel que le produit xy soit égal à 1. En d'autres termes, x admet un unique inverse pour la multiplication.
: pour tout x réel non nul, il existe un unique réel y non nul tel que le produit xy soit égal à 1. En d'autres termes, x admet un unique inverse pour la multiplication.Symboles arithmétiques
Ces symboles sont utilisés pour simplifier l'écriture de longues séries (par exemple en évitant d'utiliser des pointillés). On utilise dans chacun de ces cas une variable dite variable muette qui va prendre des valeurs dans un ensemble précis. Cette variable muette va alors permettre la description d'un terme générique placé après le symbole.
Somme
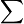 (Lettre grecque : Sigma majuscule)
(Lettre grecque : Sigma majuscule)
- Exemple
- Si n est un entier strictement positif :
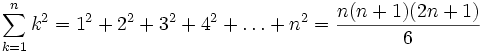
- Ici k est la variable muette, elle prend ses valeurs dans l'ensemble [1,n] (ensemble d'entiers). Le terme général de cette somme est k2.
- Autre exemple
- Ω étant l'ensemble des entiers pairs positifs
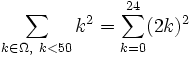
- Ici k appartient à un ensemble défini par deux conditions : ses éléments sont des entiers positifs pairs et ils sont strictement plus petits que 50
- Exemple de somme infinie
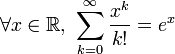
- On aurait pu écrire de manière moins condensée :
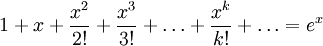
Produit
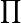 (Lettre grecque : Pi majuscule)
(Lettre grecque : Pi majuscule)Ce symbole s'utilise de manière analogue au symbole somme.
- Exemple
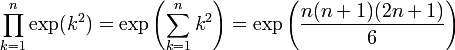
- On aurait pu écrire de manière moins condensée :
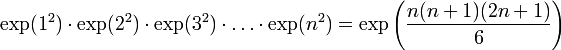
Voir aussi
- Table des symboles mathématiques
- Liste des abréviations en mathématiques
- Algèbre de Boole
- Logique mathématique
- Calcul des propositions
- Calcul des prédicats
- Portail des mathématiques
Catégories : Vocabulaire des mathématiques | Logique mathématique | Algèbre générale | Langage formel
Wikimedia Foundation. 2010.