- Style de Fitch pour la deduction naturelle
-
Style de Fitch pour la déduction naturelle
Le logicien Fitch a proposé une variante de la déduction naturelle où les démonstrations sont présentées de façon linéaire, renonçant à la structure arborescente proposée par Gentzen.
Sommaire
Introduction
Les règles exposées dans ce paragraphe sont celles du calcul des propositions. Elles permettent d’enchaîner logiquement les phrases, c’est-à-dire d'introduire de nouvelles phrases comme conséquences logiques de ce qui a été dit auparavant. À chacun des opérateurs logiques fondamentaux sont associées deux règles de déduction. L'une des règles est une règle d'introduction : elle explique comment prouver une proposition possédant l'opérateur. L'autre règle est une règle d'élimination : elle explique comment utiliser une proposition possédant l'opérateur pour poursuivre le raisonnement.
Introduction et élimination sont nécessaires pour pouvoir démonter et remonter des formules. La recherche d’une déduction logique consiste justement à analyser les prémisses, c’est-à-dire à les démonter, et à réassembler les morceaux pour faire des formules que l’on peut enchainer logiquement jusqu’à la conclusion. On croit parfois qu’il est très difficile de faire des preuves mathématiques, mais dans son principe, ce n’est pas très différent d’un jeu de construction avec des cubes.
Les règles relatives à l'implication
La règle d'introduction de l'implication ou règle de l'abandon d'une hypothèse provisoire énonce que, pour prouver une implication « si P alors Q », il suffit de procéder de la façon suivante : on pose P comme hypothèse provisoire, on fait alors des déductions à partir de toutes les phrases antérieures plus P en vue d’atteindre Q. Une fois Q atteint, on peut alors en déduire « si P alors Q ». Insistons sur un point : Q est démontrée sous l’hypothèse P mais « si P alors Q », elle, ne dépend que des prémisses antérieures. Si on utilise la méthode de Fitch, on peut introduire n’importe quand dans une déduction une hypothèse provisoire. Il suffit de la décaler vers la droite par rapport aux autres prémisses. Tout ce qui est déduit sous une hypothèse provisoire doit être sous elle ou sur sa droite mais jamais sur sa gauche. La règle d'introduction permet de conclure qu'on a prouvé « si P alors Q » sans l'hypothèse P. On peut décaler « si P alors Q » sur la gauche par rapport à P, mais pas par rapport aux autres prémisses utilisées dans la démonstration de Q. On notera :
-
 (hypothèse provisoire)
(hypothèse provisoire) (propriété déduite de 1)
(propriété déduite de 1)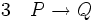 (introduction de l'implication entre les deux lignes 1 et 2)
(introduction de l'implication entre les deux lignes 1 et 2)
La règle d'élimination de l'implication, ou règle du détachement ou du modus ponens énonce que, des deux phrases « P » et « si P alors Q » on peut déduire « Q ». Elle permet de passer de conditions déjà connues, P, à des conditions nouvelles, Q, pourvu qu’il y ait une loi qui l’autorise, « si P alors Q », ce qui sera noté :
-
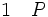
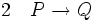
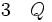 (élimination de l'implication entre les lignes 1 et 2)
(élimination de l'implication entre les lignes 1 et 2)
Montrons par exemple qu’avec ces deux règles on peut déduire « si P alors R » à partir des deux phrases « si P alors Q » et « si Q alors R » :
-
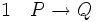 (hypothèse)
(hypothèse)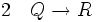 (hypothèse)
(hypothèse) (hypothèse provisoire)
(hypothèse provisoire) (modus ponens sur 3 et 1)
(modus ponens sur 3 et 1) (modus ponens sur 4 et 2)
(modus ponens sur 4 et 2)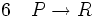 (règle d'introduction de l'implication entre 3 et 5, abandon de l’hypothèse provisoire P).
(règle d'introduction de l'implication entre 3 et 5, abandon de l’hypothèse provisoire P).
Les règles relatives à la conjonction
Pour la conjonction, les règles sont très simples.
La règle d'introduction de la conjonction énonce que, à partir des deux phrases A et B on peut déduire la phrase (A et B).
-
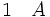
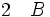
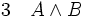 (introduction de la conjonction entre 1 et 2)
(introduction de la conjonction entre 1 et 2)
La règle d'élimination de la conjonction énonce que, à partir de la phrase (A et B), on peut déduire les deux phrases A et B prises séparément.
-
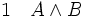
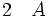 (élimination de la conjonction 1)
(élimination de la conjonction 1)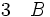 (élimination de la conjonction 1)
(élimination de la conjonction 1)
Ces règles permettent d'assembler ou au contraire de séparer des assertions qui sont toutes considérées comme vraies. C’est la forme logique de la capacité de la raison à analyser le monde, c’est-à-dire à étudier ses parties séparément, et à le synthétiser, c’est-à-dire à rassembler les éléments d’une étude en un tout. C’est pourquoi ces règles sont également appelées les règles de l'analyse et de la synthèse.
Les règles relatives à la disjonction
Les deux règles de déduction pour la disjonction sont les suivantes.
La règle d'introduction de la disjonction ou règle de l'affaiblissement d'une thèse énonce que, à partir de la phrase P on peut déduire la phrase (P ou Q) aussi bien que la phrase (Q ou P), quelle que soit la phrase Q. Cette règle peut sembler peu intéressante mais elle est en vérité très importante. Parfois il est avantageux de déduire (P ou Q) après avoir prouvé P, car on peut savoir par ailleurs que (P ou Q) a d'autres conséquences.
-
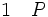
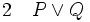 (introduction de la disjonction à partir de 1)
(introduction de la disjonction à partir de 1)
et de même
-
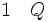
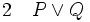 (introduction de la disjonction à partir de 1)
(introduction de la disjonction à partir de 1)
La règle d'élimination de la disjonction ou règle de la disjonction des hypothèses ou règle de la distinction des cas, stipule que, si on a prouvé (P ou Q) et qu'on a également prouvé (si P alors R) ainsi que (si Q alors R), alors on a prouvé R. Cette règle sert quand on examine plusieurs cas possibles qui conduisent à la même conclusion.
-
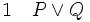
 (hypothèse provisoire)
(hypothèse provisoire) (propriété déduite de 2)
(propriété déduite de 2)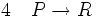 (introduction de l'implication entre 2 et 3)
(introduction de l'implication entre 2 et 3) (hypothèse provisoire)
(hypothèse provisoire) (propriété déduite de 5)
(propriété déduite de 5)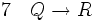 (introduction de l'implication entre 5 et 6)
(introduction de l'implication entre 5 et 6)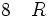 (élimination de la disjonction entre 1, 4, 7)
(élimination de la disjonction entre 1, 4, 7)
Les règles relatives à la négation
La règle d'introduction de la négation énonce que, si on démontre une contradiction à partir d’une hypothèse P alors celle-ci est nécessairement fausse et donc sa négation est vraie. Ainsi, si dans une déduction sous l’hypothèse provisoire P, on a trouvé une contradiction (Q et non Q), notée également
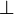 , alors on peut déduire nonP à partir de toutes les prémisses antérieures sauf P. Avec la méthode de Fitch, on décale donc (non P) sur la gauche par rapport à P, ce qui se représente comme suit :
, alors on peut déduire nonP à partir de toutes les prémisses antérieures sauf P. Avec la méthode de Fitch, on décale donc (non P) sur la gauche par rapport à P, ce qui se représente comme suit :-


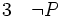 (introduction de la négation entre 1 et 2)
(introduction de la négation entre 1 et 2)
La règle d'élimination de la négation ou règle de la suppression de la double-négation ou raisonnement par absurde énonce que, de (non nonP) on peut déduire P. Il s'agit bien du raisonnement par l'absurde car dans, un tel raisonnement, pour prouver P, on suppose (non P) et l'on cherche à obtenir une contradiction. Si tel est le cas, on a prouvé (non non P) d'après la règle d'introduction de la négation, et c'est bien la règle de suppression de la double-négation qui permet de conclure à P :-
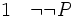
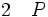 (élimination de la double négation 1)
(élimination de la double négation 1)
ou bien
-
 (hypothèse provisoire [raisonnement par l'absurde])
(hypothèse provisoire [raisonnement par l'absurde])
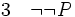 (introduction de la négation entre 1 et 2)
(introduction de la négation entre 1 et 2)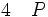 (élimination de la double négation 3)
(élimination de la double négation 3)
Quand on considère que toute phrase est nécessairement ou bien vraie ou bien fausse, la validité de cette dernière règle est évidente. Elle est caractéristique de la logique classique, qui est présentée ici et est utilisée par la grande majorité des scientifiques. Elle est parfois contestée à cause d’un problème important, celui des preuves d’existence par l’absurde. Il arrive que l’on puisse prouver qu’un problème a une solution sans être capable de la trouver. Pour cela il suffit de prouver que l’absence de solution conduit à une contradiction. Le raisonnement par l’absurde permet alors de conclure qu’il n’est pas vrai que le problème n’a pas de solution : non non (le problème a une solution). En logique classique, on supprime la double négation pour en conclure que le problème a une solution. Cependant, la démarche ainsi suivie ne fournit aucun procédé constructif de la solution cherchée. Cette objection fut soulevée par certains mathématiciens et logiciens, dont Brouwer, qui contestèrent cette méthode et s'opposèrent à Hilbert qui la défendait. Les mathématiciens constructivistes ou intuitionnistes estiment qu’une preuve d’existence n’a pas de sens si elle ne fournit pas également un procédé constructif de l'objet en question. Aussi ces derniers rejettent-ils la règle de suppression de la double négation pour lui substituer la règle suivante : de P et (non P), on peut déduire une contradiction, et de cette contradiction n'importe quelle proposition Q.
-
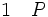
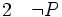
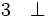
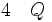 (élimination de la négation 2 en logique intuitionniste)
(élimination de la négation 2 en logique intuitionniste)
Dans les exemples, nous utiliserons cette deuxième règle d'élimination lorsqu'il est possible de se passer de la règle d'élimination de la double négation
On peut introduire d’autres règles pour les autres opérateurs booléens, notamment l’opérateur d’équivalence, mais ce n’est pas nécessaire, parce que ces opérateurs peuvent être définis à partir des précédents et que leurs règles de déduction peuvent être alors déduites à partir des règles précédentes. (P équivaut à Q) est défini par ( (si P alors Q) et (si Q alors P) ) .
Exemples
Nous donnons ci-dessous quelques exemples d'utilisation de la déduction naturelle. Dans la première partie, nous n'utiliserons pas la règle d'élimination de la double négation. Dans la deuxième partie, nous utiliserons cette règle. Les formules déduites dans cette deuxième partie ne sont pas reconnues valides par les mathématiciens intuitionnistes. Nous utiliserons les symboles suivants :
 pour si ... alors ...,
pour si ... alors ..., 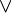 pour ou,
pour ou, 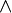 pour et,
pour et,  pour non. Le symbole
pour non. Le symbole 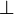 désigne une contradiction, c'est-à-dire une proposition fausse.
désigne une contradiction, c'est-à-dire une proposition fausse.Exemples n'utilisant pas l'élimination de la double négation
Exemple 1 :
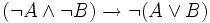
-
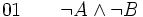 (hypothèse provisoire)
(hypothèse provisoire) (élimination de la conjonction 01)
(élimination de la conjonction 01) (élimination de la conjonction 01)
(élimination de la conjonction 01) (hypothèse provisoire)
(hypothèse provisoire) (hypothèse provisoire)
(hypothèse provisoire) contradiction entre 02 et 05
contradiction entre 02 et 05 (introduction de l'implication entre 05 et 06)
(introduction de l'implication entre 05 et 06) (hypothèse provisoire)
(hypothèse provisoire) contradiction entre 03 et 08
contradiction entre 03 et 08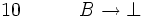 (introduction de l'implication entre 08 et 09)
(introduction de l'implication entre 08 et 09) (élimination de la disjonction entre 04, 07, 10)
(élimination de la disjonction entre 04, 07, 10)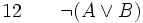 (introduction de la négation entre 04 et 11)
(introduction de la négation entre 04 et 11)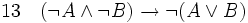 (introduction de l'implication entre 01 et 12 et fin de la déduction)
(introduction de l'implication entre 01 et 12 et fin de la déduction)
On montre que la réciproque
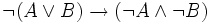 est également valide. On montre également que
est également valide. On montre également que 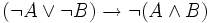 , mais pour la réciproque de cette dernière propriété, on utilise l'élimination de la double négation.
, mais pour la réciproque de cette dernière propriété, on utilise l'élimination de la double négation.
Exemple 2 :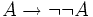
-
 (hypothèse provisoire)
(hypothèse provisoire) (hypothèse provisoire)
(hypothèse provisoire) (élimination de la négation entre 01 et 02)
(élimination de la négation entre 01 et 02)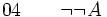 (introduction de la négation entre 02 et 03)
(introduction de la négation entre 02 et 03)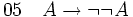 (introduction de l'implication entre 01 et 04, fin de la déduction)
(introduction de l'implication entre 01 et 04, fin de la déduction)
La réciproque
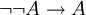 découle directement de l'élimination de la double négation et est rejetée par les intuitionnistes. Mais curieusement, il n'en est pas de même de
découle directement de l'élimination de la double négation et est rejetée par les intuitionnistes. Mais curieusement, il n'en est pas de même de 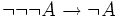 qui se prouve sans cette hypothèse, et qui, elle, est acceptée par les intuitionnistes.
qui se prouve sans cette hypothèse, et qui, elle, est acceptée par les intuitionnistes.
Exemple 3 :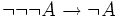
-
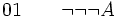 (hypothèse provisoire)
(hypothèse provisoire) (hypothèse provisoire)
(hypothèse provisoire)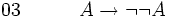 (théorème de l'exemple 2)
(théorème de l'exemple 2) (élimination de l'implication ou modus ponens entre 02 et 03)
(élimination de l'implication ou modus ponens entre 02 et 03) (élimination de la négation entre 01 et 04)
(élimination de la négation entre 01 et 04) (introduction de la négation entre 02 et 05)
(introduction de la négation entre 02 et 05)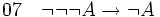 (introduction de l'implication entre 01 et 06, fin de la déduction)
(introduction de l'implication entre 01 et 06, fin de la déduction)
Exemples utilisant l'élimination de la double négation
Les exemples qui suivent utilisent l'élimination de la double négation. On peut montrer que cette utilisation est nécessaire. Ils ne sont donc pas acceptés en logique intuitionniste.
Exemple 4 :
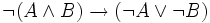
-
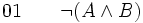 (hypothèse provisoire [raisonnement par l'absurde])
(hypothèse provisoire [raisonnement par l'absurde])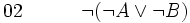 (hypothèse provisoire)
(hypothèse provisoire)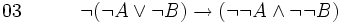 (théorème, réciproque de l'exemple 1)
(théorème, réciproque de l'exemple 1)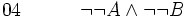 (élimination de l'implication ou modus ponens entre 02 et 03)
(élimination de l'implication ou modus ponens entre 02 et 03) (élimination de la double négation dans 04)
(élimination de la double négation dans 04) (élimination de la négation entre 01 et 05)
(élimination de la négation entre 01 et 05)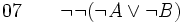 (introduction de la négation entre 02 et 06)
(introduction de la négation entre 02 et 06)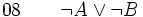 (élimination de la double négation dans 07)
(élimination de la double négation dans 07)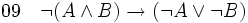 (introduction de l'implication entre 01 et 08)
(introduction de l'implication entre 01 et 08)
Exemple 5 : si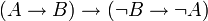 ne nécessite pas l'élimination de la double négation, celle-ci est nécessaire pour prouver la réciproque
ne nécessite pas l'élimination de la double négation, celle-ci est nécessaire pour prouver la réciproque 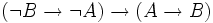 .
.Exemple 6: On peut démontrer que
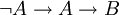 . En effet si on
. En effet si on 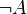 et A, on a
et A, on a 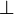 (faux) et donc on a B.
(faux) et donc on a B.Exemple 7 : de même la démonstration de la validité du tiers exclu
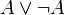 utilise l'élimination de la double négation. En supposant que
utilise l'élimination de la double négation. En supposant que 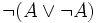 , on en déduit
, on en déduit 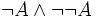 (réciproque de l'exemple 1), d'où une contradiction et la validité de
(réciproque de l'exemple 1), d'où une contradiction et la validité de 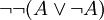 .
.Si les intuitionnistes rejettent le tiers exclu, ils acceptent bien sûr le principe de non contradiction :
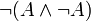 . En effet, la supposition
. En effet, la supposition 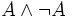 est une contradiction. On a donc
est une contradiction. On a donc 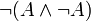 par introduction de la négation.
par introduction de la négation.
Exemple 7 connu sous le nom de loi de Peirce :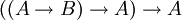 . Curieusement, bien que ne contenant pas de négation, la déduction de cette loi nécessite l'élimination de la double négation, par exemple par l'intermédiaire de l'utilisation du tiers exclu. On suppose que l'on a
. Curieusement, bien que ne contenant pas de négation, la déduction de cette loi nécessite l'élimination de la double négation, par exemple par l'intermédiaire de l'utilisation du tiers exclu. On suppose que l'on a 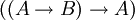 . D'après le tiers exclu:
. D'après le tiers exclu:.ou bien on a A,
.ou bien on a
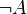 et donc on a
et donc on a 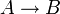 (exemple 6) et puisqu'on a
(exemple 6) et puisqu'on a 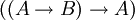 avec le modus ponens, on a A.
avec le modus ponens, on a A.Les règles de déduction pour les quantificateurs
L’usage des noms de variable dans les théories du premier ordre
Les règles de déduction pour les opérateurs universels et existentiels gouvernent l’usage des noms de variable. Cet usage donne à une théorie la puissance de la généralité, c’est-à-dire la possibilité de connaître non chaque invividu pris isolément mais tous les individus d’un même genre, en une seule phrase.
Les règles d’usage des variables précisent à quelles conditions on peut introduire des noms de variable et ce qu’on peut alors dire à leur sujet. Ces règles sont naturelles mais il y a quelques difficultés techniques à propos des notions de terme, d’occurrence libre ou liée d’une variable, de substitution d’un terme aux occurrences d’une variable et de substitution d’une variable aux occurrences d’un terme.
Pour qu’une théorie puisse utiliser la logique du premier ordre il faut avoir défini un domaine d’objets et il faut que les prédicats attribués par la théorie à ses objets ne soient pas eux-mêmes des objets de la théorie.
La signification d’un nom de variable d’objet, c’est de représenter un objet quelconque de la théorie : soit x un nombre. Souvent on introduit un nom de variable dans des prémisses qui déterminent des conditions générales sur cet objet. x est un objet quelconque de la théorie pourvu seulement qu’il satisfasse à ces conditions : soit x un nombre premier ... Une théorie contient en général des noms pour ses objets. La théorie des nombres entiers contient par exemple des noms pour tous les nombres : 0, 1, 2, ..., -1, -2, ...
Les termes peuvent être simples ou composés. Ce sont les noms d’objet, les noms de variable d’objet, et toutes les expressions composées que l’on peut former à partir d’eux en appliquant les opérateurs d’objets de la théorie. Par exemple, 1, x, x+1et (x+x)+1 sont des termes de la théorie des nombres.
Rappelons d’abord la très importante distinction entre les variables liées par un opérateur et les autres, les variables libres. Les occurrences d’un nom de variable dans une phrase sont tous les endroits où ce nom apparait. Une occurrence peut être libre ou liée. Quand un opérateur existentiel ou universel en x est appliqué à une phrase complexe, toutes les occurrences de x deviennent liées par cet opérateur. Toutes les occurrences qui ne sont pas ainsi liées sont libres.
Si une phrase contient plusieurs opérateurs existentiels et universels, il est souhaitable que ces opérateurs portent tous sur des noms de variable différents. Cette règle n’est pas indispensable. Elle n’est pas respectée lorsque l’on met le calcul des prédicats sous la forme d’une algèbre cylindrique (une algèbre cylindrique est une algèbre de Boole complétée par des lois particulières aux opérateurs universels et existentiels). Mais elle est toujours respectée en pratique parce qu’elle permet d’éviter des confusions.
Une phrase est obtenue à partir d’une autre par substitution d’un terme t aux occurrences d’une variable x lorsque toutes les occurrences libres de x ont été remplacées par t. Par exemple, (le père de x est humain et le père de x est honnête) est obtenu par substitution du terme le père de x à la variable y dans la formule (y est humain et y est honnête).
Ces préliminaires permettent de formuler les règles de déduction pour les opérateurs universels et existentiels.
Les règles relatives au quantificateur universel
La règle d'introduction du quantificateur universel ou règle de généralisation énonce que, de P(x) on peut déduire (pour tout x, P(x)) pourvu que le nom de variable x n’apparaisse jamais dans les hypothèses dont P(x) dépend.
-
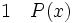
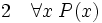 (introduction de quel que soit, où x n'est pas libre dans les prémisses de P)
(introduction de quel que soit, où x n'est pas libre dans les prémisses de P)
Très souvent on introduit des variables dans des hypothèses provisoires. On raisonne ensuite sur elles comme si elles étaient des objets. On peut alors en déduire des lois générales, parce que ce qu’on a déduit est vrai pour tous les objets qui vérifient les mêmes hypothèses. Ce sont les règles d’abandon d’une hypothèse provisoire et de généralisation qui permettent de conclure.
La règle d'élimination du quantificateur universel ou règle de singularisation énonce que, à partir d’une phrase de la forme (pour tout x) P(x), on peut déduire P(t), pour n’importe quel terme t dont les variables ne sont pas liées dans P(x). P(x) désigne une phrase quelconque qui contient x comme variable libre, P(t) désigne la phrase obtenue à partir de P(x) en y substituant t à toutes les occurrences libres de x. La règle de singularisation consiste simplement à appliquer une loi universelle à un cas singulier.
-
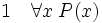
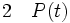 (élimination de quel que soit)
(élimination de quel que soit)
Les règles relatives au quantificateur existentiel
La règle d’introduction du quantificateur existentiel, ou règle des preuves directes de l’existence, énonce que, à partir de la phrase P(t), on peut déduire il existe un x tel que P(x) pour toute variable x qui n’apparait pas dans P(t) et pour tout terme t dont les noms de variables ne sont pas liés dans P(x).
P(t) désigne une phrase quelconque qui contient au moins une fois le terme t. P(x) est obtenue à partir de P(t) en substituant x à t à une ou plusieurs de ses occurrences. Dans cette règle il n’est pas nécessaire de substituer x à toutes les occurrences de t.
-
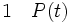
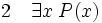 (introduction de il existe)
(introduction de il existe)
La règle d'élimination du quantificateur existentiel ou règle des conséquences de l’existence permet, à partir d'une proposition (il existe x, P(x)), d'introduire une nouvelle hypothèse provisoire P(y) où y est un nom de variable qui n’a jamais été utilisé auparavant et où P(y) est obtenu à partir de P(x) en substituant y à toutes les occurrences de x. On peut alors raisonner sous cette hypothèse. La règle des conséquences de l’existence permet alors de conclure de la façon suivante : de la phrase (il existe un x tel que P(x)) on peut déduire R lorsque R a été déduit sous l’unique hypothèse provisoire supplémentaire P(y) et que y n’apparait ni dans les prémisses antérieures à P(y) ni dans R. y est une sorte d’être hypothétique. Il ne fait que servir d’intermédiaire dans une déduction mais il n’apparait ni dans ses prémisses, ni dans sa conclusion.-
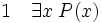 (hypothèse)
(hypothèse)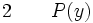 (y variable nouvelle)
(y variable nouvelle) (déduction à partir de 2, ne faisant pas intervenir y)
(déduction à partir de 2, ne faisant pas intervenir y)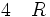 (élimination de il existe dans 1 et 3)
(élimination de il existe dans 1 et 3)
Exemples
Exemple 1
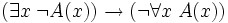
-
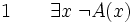 (hypothèse provisoire)
(hypothèse provisoire)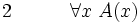 (hypothèse provisoire)
(hypothèse provisoire) (y variable nouvelle à partir de 1)
(y variable nouvelle à partir de 1) (élimination de quel que soit dans 2)
(élimination de quel que soit dans 2) (élimination de la négation 3, 4)
(élimination de la négation 3, 4) (élimination de il existe entre 1 et 5)
(élimination de il existe entre 1 et 5)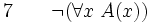 (introduction de la négation entre 2 et 6)
(introduction de la négation entre 2 et 6)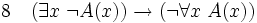 (introduction de l'implication 1, 7)
(introduction de l'implication 1, 7)
Exemple 2 : on a également
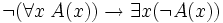 , mais la preuve nécessite une élimination de la double négation, et ce théorème de la logique classique n'est pas accepté en logique intuitionniste.
, mais la preuve nécessite une élimination de la double négation, et ce théorème de la logique classique n'est pas accepté en logique intuitionniste.Comment vérifier la correction d’un raisonnement ?
A ces douze règles, ou quatorze, si on compte que la règle d'éliminination de la conjonction est en fait une double règle, et de même pour la règle d'introduction de la disjonction, il faut en ajouter une quinzième, très simple, la règle de répétition : on peut toujours répéter une thèse antérieure, sauf si elle dépend d’une hypothèse qui a été abandonnée. On peut donc répéter toutes les thèses tant qu’on ne les décale pas sur la gauche. Cette règle est nécessaire quand on veut répéter une prémisse dans une conclusion ou quand on a besoin d’une thèse antérieure dans le corps d’une déduction sous hypothèse provisoire pour appliquer une règle.
La liste des quinze règles précédentes est complète au sens où elle suffit pour faire toutes les déductions correctes. Kurt Gödel a prouvé, (Théorème de complétude) pour un système logique différent, mais équivalent à celui qui vient d’être présenté, qu’il suffit pour formaliser toutes les déductions correctes du Calcul des prédicats du premier ordre.
Les déductions correctes sont d’abord toutes celles qui respectent rigoureusement ces règles fondamentales. Toutes les phrases doivent être ou bien des axiomes, ou bien des hypothèses provisoires, ou bien des conséquences des phrases qui les précèdent en vertu de l’une des quinze règles. Par souci de rapidité, on peut également utiliser des règles dérivées (par exemple faire suivre
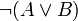 par
par 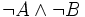 ). Une règle dérivée est correcte lorsqu’on peut montrer que tout ce qui peut être déduit avec elle peut aussi être déduit sans elle avec seulement les règles fondamentales.
). Une règle dérivée est correcte lorsqu’on peut montrer que tout ce qui peut être déduit avec elle peut aussi être déduit sans elle avec seulement les règles fondamentales.Tant que les déductions sont formalisées, il est toujours possible de reconnaitre, y compris par un programme, si une déduction est correcte parce que les règles de déduction sont en nombre fini et qu’il est toujours possible de vérifier en un temps fini si une formule est la conséquence d’une ou plusieurs autres en vertu de l’une de ces règles. Cette démarche réalise une partie du programme appelé parfois finitaire proposé par David Hilbert pour résoudre les problèmes des fondements des mathématiques. Hilbert cherchait une méthode efficace qui permette de décider pour tout énoncé mathématique s'il est un théorème, c’est-à-dire une vérité mathématique. Le calcul des prédicats permettait de ramener le problème à la question de savoir si une formule est une loi logique ou non.
Mais s'il est possible de vérifier la validité d'une déduction conduisant à une formule, à l'inverse, la question de savoir si une formule donnée est une loi logique ou non ne peut être résolue en général. En effet, il n’existe pas de méthode universelle permettant de dire si une formule est une loi logique ou non. Cet inexistence se déduit du théorème d'incomplétude de Gödel. On dit que la question de savoir si une formule est une loi logique est indécidable.
La vérification de la correction des déductions dans la langue courante pose davantage de difficultés. Il faut d’abord traduire les phrases familières dans une langue formalisée du calcul des prédicats. Cette étape pose parfois problème si on a des doutes sur la fidélité de la traduction. Mais la plus grosse difficulté vient de ce que les déductions courantes font en général une large place à l’implicite. Même les relations de dépendance par rapport à une hypothèse ne sont pas toujours explicitées. Les déductions formelles au contraire ne laissent rien dans l’ombre. Celles qui sont ici proposées sont très semblables aux déductions courantes sauf qu’elles explicitent tout. Afin de certifier correct les raisonnements et démonstrations usuels il faut expliciter de tout ce qui est implicite. C’est pourquoi souvent il faut beaucoup étudier et connaître tout l’implicite avant de savoir si un raisonnement est correct.
- Portail des mathématiques
- Portail de la logique
Catégories : Logique mathématique | Logique | Méthode de démonstration -
Wikimedia Foundation. 2010.
