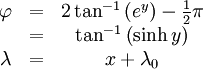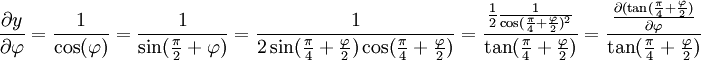- Projection de mercator
-
Projection de Mercator
La projection de Mercator est cylindrique.
La projection de Mercator avec les indicatrices de déformation de Tissot.La projection de Mercator est une projection cylindrique du globe terrestre sur une carte plane formalisée par Gerardus Mercator en 1569. Les parallèles et les méridiens sont des lignes droites et l'inévitable étirement Est-Ouest en dehors de l'équateur est accompagné par un étirement Nord-Sud correspondant, de telle sorte que l'échelle Est-Ouest est partout semblable à l'échelle Nord-Sud. Une carte de Mercator ne peut couvrir les pôles : ils seraient infiniment hauts.
La projection de Mercator de 1569.Il s'agit d'une projection conforme, c’est-à-dire qu'elle conserve les angles. Toute ligne droite sur une carte de Mercator est une ligne d'azimut constant, c'est à dire une loxodromie. Ceci la rend particulièrement utile aux marins, même si le trajet ainsi défini n'est généralement pas sur un grand cercle et n'est donc pas le chemin le plus court.
À l'époque des grands voiliers, la durée du voyage était soumise aux éléments, et donc la distance du trajet était moins importante que la direction, surtout parce que la longitude était difficile à calculer précisément.
Les cartes traditionnelles inspirées des travaux de Mercator destinés à la navigation ont pour principal défaut de donner une idée erronée des surfaces occupées par les différentes régions du monde, et donc des rapports entre les peuples.
Quelques exemples :
L’Amérique du Sud semble plus petite que le Groenland ; en réalité, elle est neuf fois plus grande : 17,8 millions de km² contre 2,1 millions. L’Inde (3,3 millions de km²) semble plus petite que la Scandinavie (1,1 million de km²). L’Europe (9,7 millions de km²) semble plus étendue que l’Amérique du Sud, pourtant près de deux fois plus grande.
Sommaire
Formules
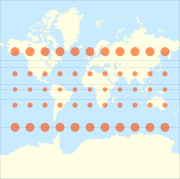
Les équations suivantes déterminent les coordonnées x et y d'un point sur une carte de Mercator à partir de sa latitude φ et de sa longitude λ (avec λ0 au centre de la carte)
Et voici la fonction dite fonction de Gudermann inverse :
Exemple d'application
Soit la carte illustrant cet article (ayant une hauteur h = 724 et une largeur w = 679 (en pixels). La carte est centrée sur latitude 0, longitude 0. Le pixel 0,0 est en haut à gauche.
Pour obtenir la position du pixel horizontal représentant la longitude λ (en degrés), il suffit d'appliquer la formule donnée précédemment :
pixel_x = w*((λ+180) / 360).
Pour obtenir la position du pixel vertical de la latitude φ (en degrés) :
pixel_y = h / 2-LN(TAN( (pi / 4) + RADIANS(φ) / 2))*ratio
avec ratio = w / (pi*2) = 108
Calcul
Puisqu'on utilise une projection cylindrique, x ne dépend que de λ et y ne dépend que de φ. L'échelle Nord-Sud (en φ) doit être partout égale à l'échelle Est-Ouest (en λ), mais un radian de longitude ne fait pas la même taille aux pôles qu'à l'équateur. Le rapport des dérivées doit donc être égal au rapport de la longueur du parallèle par rapport à la longueur du méridien.
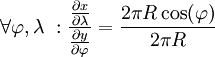
Et puisque l'on choisit
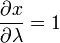
On trouvepuis en intégrant
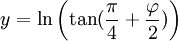
Bibliographie
Portail de la géographie
Portail de la géométrie
Catégorie : Projection cartographique
![\begin{matrix}
x &=& \lambda - \lambda_0
\\ y &=& \ln \left[ \tan \left( \frac {1} {4} \pi + \frac {1} {2} \varphi \right) \right]
\\ \ & =& \frac {1} {2} \ln \left( \frac {1 + \sin \varphi} {1 - \sin \varphi} \right)
\\ \ & =& \sinh^{-1} \left( \tan \varphi \right)
\\ \ & =& \tanh^{-1} \left( \sin \varphi \right)
\\ \ & =& \ln \left( \tan \varphi + \sec \varphi \right)
\end{matrix}](/pictures/frwiki/99/c6b24447b12b2931cebfb19c3457096a.png)
Wikimedia Foundation. 2010.
