- Programmation par contrainte
-
Programmation par contraintes
La programmation par contraintes (PPC, ou CP pour Constraint Programming en anglais) consiste à poser un problème sous forme de relations logiques (appelées contraintes) entre plusieurs variables. Un problème formulé de la sorte comporte donc un certain nombre de ces variables, chacune ayant un domaine (i.e. un ensemble de valeurs possibles), et un certain nombre de contraintes. Le domaine d'une variable peut être fini (intervalle de nombres entiers, intervalle d'ensembles par exemple) ou continu.
Une contrainte implique une ou plusieurs variables, et restreint les valeurs que peuvent prendre simultanément ces variables. Lorsqu'une contrainte implique deux (respectivement n) variables, on parle de contrainte binaire (respectivement n-aire). Lorsqu'elle implique un nombre non fixé de variables, on parle de contrainte globale.
Trouver une solution à un problème de PPC consiste à décider s'il existe ou non une affectation de toutes les variables telle que l'ensemble des contraintes du problème soient satisfaites.
Sommaire
Programmation par contraintes sur les domaines finis
Dans le cas de la résolution sur domaines finis, il est en théorie possible d'énumérer toutes les possibilités et de vérifier si elles violent ou non les contraintes, cette méthode est appelée générer et tester. Cependant, cela s'avère impraticable pour des problèmes de taille moyenne en raison du grand nombre de combinaisons possibles. Une des majeures parties de la résolution, appelée « filtrage », a pour but d'éviter cette énumération exhaustive. Elle consiste à déduire à partir des contraintes les valeurs impossibles. Lorsqu'une variable ne possède plus qu'un candidat, celle-ci est instanciée (i.e. cette valeur lui est affectée). Cependant, le filtrage seul ne permet pas d'instancier toutes les variables, et il est donc nécessaire de scinder le problème en plusieurs parties (par exemple en instanciant une variable à chacune de ses valeurs possibles) et relancer le filtrage sur l'une de ces parties et ce, de manière récursive jusqu'à obtenir l'instanciation de toutes les variables. Lorsque le filtrage détecte que l'instanciation partielle viole une contrainte, on utilise généralement alors un mécanisme de retour sur trace afin de remettre en cause le dernier choix effectué.
Cette série de découpages du problème peut être représentée sous forme d'un arbre. Le but de la recherche est de parcourir cet arbre (en le construisant au fur et à mesure) jusqu'à trouver une solution au problème tandis que le filtrage consiste à « élaguer » cet arbre en supprimant toutes les parties n'aboutissant qu'à des contradictions.
Algorithmes de recherche
(TODO : algorithmes top-down : différents parcours, algorithmes Bottom-up, éventuellement parler des méthodes incomplètes)
Filtrage
Le filtrage consiste à supprimer d'un problème de PPC des valeurs de variables ne pouvant pas prendre part à une solution. Pour accélérer la recherche d'une solution d'un problème, il est nécessaire d'obtenir un bon compromis entre le temps nécessaire au filtrage et l'efficacité de celui-ci. C'est pourquoi il existe plusieurs niveaux d'efficacités de filtrage, capables de retirer plus ou moins de valeurs, pour un coût en temps plus ou moins élevé. Étant donné que toutes les contraintes d'un problème de PPC doivent être satisfaites, le fait pour une valeur d'une variable de ne pas pouvoir satisfaire une seule contrainte du problème implique qu'elle ne pourra prendre part à aucune solution du problème. Il est donc possible de raisonner séparément sur chaque contrainte afin de pouvoir trouver des valeurs pour lesquelles cette contrainte ne peut être satisfaite, et donc les retirer du problème entier.
On appelle consistance locale le fait de vérifier que certaines variables ne violent pas les contraintes qui lui sont liées. On ignore alors les autres variables et contraintes. Cela permet de filtrer alors certaines valeurs impossibles pour un coût réduit. Il existe plusieurs consistances locales, offrant chacune un équilibre différent entre efficacité du filtrage et rapidité de calcul.
Consistance de nœud
Elle consiste à ne considérer qu'une seule variable. On retire alors toutes les valeurs pour lesquelles au moins une contrainte est impossible à satisfaire. Ce filtrage est très rapide, mais peu efficace (étant donné qu'on ne considère aucune autre variable impliquée dans la contrainte).
Consistance d'arc
La consistance d'arc, en anglais Arc Consistency (AC) consiste, pour chaque contrainte binaire (i.e. impliquant deux variables) à supprimer du domaine d'une variable toute valeur qui ne peut pas satisfaire la contrainte étudiée au vu des valeurs encore possibles pour l'autre variable. Par exemple, soient V1 ∈ [1,2,3] et V2 ∈ [1,3] avec la contrainte V1 = V2. On a alors les solutions 1-1 et 3-3. La valeur 2 de V1 n'appartenant pas à une solution, on la supprime du domaine.
Consistance d'hyperarc
Aussi appelée Hyperarc Consistency (HAC), c'est une généralisation de la consistance d'arc pour les contraintes non binaires. Elle a aussi été appelée consistance d'arc généralisée. Le principe est le même que pour les contraintes binaires : une contrainte est HAC si et seulement si chaque valeur de chaque variable appartient à une solution de la contrainte. On établit la consistance d'hyperarc en supprimant toutes les valeurs qui ne satisfont pas cette propriété.
Par exemple, la contrainte Alldiff impliquent que les variables sur lesquelles elle est définie prennent des valeurs deux à deux différentes. On sait établir efficacement la consistance d'hyperarc pour cette contrainte.
k-consistance
Elle consiste à considérer k variables, et de tester tous les k-uplets de valeurs possibles afin de tester s'ils ne violent pas les contraintes. Plus k est grand, plus le filtrage sera efficace. Cependant, du fait du grand nombre de combinaisons à tester, cela reste souvent trop lourd. La 3-consistence donne de bons résultats, cependant du fait de la complexité de son implémentation, elle n'est que très rarement présente dans des solveurs de contraintes.
La 2-consistence est en fait une autre vue de la consistance d'arc. Si un problème contient n variables, alors la n-consistance consisterait à tester l'ensemble des possibilités.
Consistance de bornes
Lorsque les domaines des variables sont trop grands (plusieurs milliers d'éléments), le fait de stocker l'appartenance ou non de chaque valeur au domaine de la variable peut se révéler trop lourd à traiter. On utilise dans ce cas la consistance de bornes, qui consiste à simplement raisonner sur les valeurs minimum et maximum que les variables peuvent prendre. Pour certaines contraintes, comme par exemple celles d'inégalité ( X < Y ), la consistance de bornes est très proche, voire équivalente, à la consistance d'arc.
Algorithmes de filtrage
AC1, AC2, AC3, AC4, AC5, AC6, AC7, AC8, AC2001
Exemples de problèmes
N-Dames
Le problème des N-Dames consiste à placer N dames sur un échiquier NxN sans que l'une d'elles puisse en prendre une autre (avec les règles des échecs : une dame peut prendre toute pièce située sur sa ligne, sur sa colonne ou sur l'une de ses deux diagonales).
Le problème peut être représenté avec N variables (Vi ∈ [1..N], i=1 .. N), représentant la position en colonne de la dame de la ligne i. En effet, comme deux dames ne peuvent pas être sur la même ligne, et qu'il y a autant de dames que de lignes, il y a exactement une et une seule dame par ligne.
Les contraintes imposées sur les variables Vi sont :
pour tout i ≠ j :
- Vi ≠ Vj (ne pas mettre deux dames sur la même colonne).
- Vi - i ≠ Vj - j (ne pas mettre deux dames sur la même diagonale NO-SE)
- Vi + i ≠ Vj + j (ne pas mettre deux dame sur la même diagonale NE-SO)
Méthode de résolution
Le problème étant défini sur un produit d'ensembles de cardinal fini, il peut se résoudre par une énumération complète des valeurs des variables.
En pratique, on construit un arbre de recherche, dont les nœuds correspondent à une variable, et chaque branche à une réduction du domaine de la variable (cette réduction pouvant être une instanciation, c’est-à-dire la réduction du domaine à un singleton).
À chaque énumération (une feuille terminale de l'arbre de recherche), une vérification du respect de chaque contrainte doit être réalisée.
Au total, si chaque variable a un domaine de cardinal supérieur ou égal à C, alors l'énumération comporte au moins Cn étapes.
Cette méthode fait une utilisation trop pauvre des contraintes, ce qui conduit à explorer un trop grand nombre de combinaisons. Dans l'exemple des N-reines décrit ci-dessus, on s'aperçoit en effet que si à un nœud de l'arbre, une variable Vi a été instanciée à une valeur x, il est inutile d'explorer toute sous-branche où une variable Vj, j ≠ i serait instanciée à la même valeur x.
On peut ainsi limiter la taille de l'espace des recherches en faisant un usage efficace des capacités de déduction des contraintes : on appelle cette méthode la propagation de contraintes. Dans cette méthode, on peut voir le problème de PPC comme un réseau de variables qui communiquent entre elles par le seul intermédiaire des contraintes :
- lorsque le domaine d'une variable est réduit, on « réveille » les contraintes qui impliquent cette variable.
- lorsqu'une contrainte est réveillée, on examine s'il est possible de faire des déductions sur le domaine des autres variables de la contrainte.
Les domaines et les contraintes étant en nombres finis, ce processus converge toujours vers, soit une contradiction (une variable a un domaine vide, ce qui signifie que le problème n'a pas de solution), soit vers un point fixe (toutes les déductions possibles ayant été faites, il n'y a plus lieu de réduire plus avant les domaines des variables).
À l'issue de ce processus, trois cas de figure se présentent :
- Si une contradiction a été identifiée, il faut remonter d'un niveau dans l'arbre de recherche (backtracking).
- Si le domaine de chaque variable est un singleton, c'est qu'une solution a été trouvée. On peut alors s'arrêter si l'on cherche une solution, ou continuer le parcours de l'arbre d'énumération si l'on cherche toutes les solutions.
- Si le domaine d'une variable comporte plusieurs valeurs, il faut poursuivre l'énumération par une descente dans l'arbre de recherche.
send+more=money
Soit l'équation :
send +more ----- money
Le but est d'associer un chiffre à chaque lettre tel que la somme soit vérifiée. Les variables sont donc s, e, n, d, m, o, r et y toutes étant des entiers dans [0,9]. On pose la contrainte
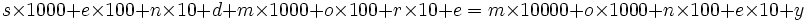 .
.Sudoku
Le sudoku consiste à remplir une grille 9x9 avec des chiffres de 1 à 9 tel que chaque chiffre n'apparaisse qu'une seul fois dans chaque ligne, colonne, et sous-boîte de taille 3x3.
Les variables sont donc naturellement des entiers dans [1,9]. On utilise ensuite la contrainte globale AllDifferent qui est bien connue sur chaque ligne, colonne, et sous-boîte.
Autres
Reconnaissance de scènes 3D, raisonnement temporel qualitatif.
Applications
La PPC se révèle très efficace pour des problèmes d'emploi du temps et d'affectation, de ce fait elle est principalement utilisée dans le cadre de problèmes de logistique complexes.
Autres domaines de contraintes
- termes
- booléens
- réels
- intervalles
- ensembles
- chaînes
Solveurs de contraintes
- Étude théorique
- Architecture d'un solveur
- Langages d'expression des propagateurs : indexicaux, CHRs
- liens vers solveurs libres et commerciaux
- Logiciel propriétaire
- Artelys Kalis (C++, bibliothèques Java)
- Comet (Langage orienté objet dédié à la résolution de problèmes de contraintes. Gratuiciel pour usage académique.)
- Disolver (Bibliothèque C++)
- ILOG CP Optimizer et ILOG CP (bibliothèques C++, Java, .Net)
- JaCoP (Bibliothèque Java)
- Koalog Constraint Solver (Bibliothèque Java)
- Logiciel libre
- Logiciel propriétaire
Extensions
- contraintes valuées
- étude et détection des symétries
- techniques de décomposition et classes de problèmes "traitables"
- métaheuristiques
- transition de phase
Voir aussi
Articles connexes
- Propagation de contraintes
- Problème de satisfaction de contrainte
- Programmation logique
- Problème des huit dames
- Heuristique
Liens et documents externes
- AFPC : Association Française de Programmation par Contraintes
- Article sur l'utilisation du sudoku comme outil pédagogique pour la PPC
- (en) Global Constraint Catalog : Catalogue de contraintes globales riche et documenté.
Catégories : Algorithmique | Recherche opérationnelle | Paradigme de programmation | Langage de programmation logique
Wikimedia Foundation. 2010.
