Problème de satisfaction de contrainte

Les problèmes de satisfaction de contrainte ou CSP (Constraint Satisfaction Problem) sont des problèmes mathématiques où l'on cherche des états ou des objets satisfaisant un certain nombre de contraintes ou de critères. Les CSP font l'objet de recherches intenses à la fois en intelligence artificielle et en recherche opérationnelle. De nombreux CSP nécessitent la combinaison d'heuristiques et de méthodes d'optimisation combinatoire pour être résolu en un temps raisonnable.

Jean-Louis Laurière, un chercheur de Paris 6 est un des pionniers des problèmes de satisfaction de contraintes, avec en particulier le Système et language ALICE ^{[1] [2]}

Exemples

Exemples de problèmes qui peuvent être modélisés par un problème de satisfaction de contrainte :

• Problème des huit dames
• Théorème des quatre couleurs
• Sudoku
• Satisfiabilité booléenne

Les algorithmes utilisés pour résoudre des problèmes de satisfaction de contrainte inclus l'AC-3, le retour sur trace, et l'algorithme des conflits minimaux.

Définition formelle

Formellement, un problème de satisfaction de contrainte est définit par un triplet 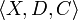, où X est un ensemble de variables, D est un domaine de valeurs, et C est un ensemble de contraintes. Chaque contrainte est à son tour une paire 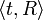, où t est un N-uplet de variables et R est un ensemble de N-uplets de valeurs; tous ces N-uplets ayant le même nombre d'éléments; ainsi R est une relation. Une évaluation des variables est une fonction des variables vers les domaines, 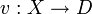. Une telle évaluation satisfait une contrainte 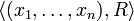si 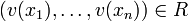. Une solution est une évaluation qui satisfait toutes les contraintes.

Aspects théoriques des CSPs

Les CSPs sont aussi étudiés en théorie de la complexité des algorithmes et en théorie des modèles finis. Une question importante est de savoir si pour chaque ensemble de relations, l'ensemble de tous les CSPs qui peuvent être représentés uniquement par des relations choisies à partir de cet ensemble est soit de classe P soit NP-complet (en présumant P ≠ NP). Si une telle dichotomie est vraie, alors les CSPs fournissent l'un des plus larges ensembles connus de NP, évitant les problèmes qui ne sont ni résolus en un temps polynomial ni NP-complet, dont l'existence fut démontrée par Ladner. Les résultats de la dichotomie sont connus pour des CSPs où le domaine de valeur est de taille 2 ou 3 mais le cas général est toujours en question.

La plupart des CSPs connus pour être facile à aborder sont ceux où l'hypergraphe de contraintes a une largeur arborescente limitée (et où il n'y a aucune restriction sur l'ensemble des relations représentant les contraintes), ou alors, les contraintes ont une forme arbitraire mais il existe essentiellement des polymorphismes non-unaires de cet ensemble de relations de contrainte.

Voir aussi

• Satisfaction de contrainte
• Programmation déclarative
• Programmation par contraintes
• Distributed Constraint Satisfaction Problem (DisCSP)

Notes et références

Liens externes

• (fr) Blaise Madeline, Algorithmes évolutionnaires et résolution de problèmes de satisfaction de contraintes en domaines finis.
• (fr) Christine Solnon, Cours : Programmation par Contraintes.
• (fr) Pierre Lopez, Le concept de contraintes : propagation, satisfaction, programmation.
• (en) Edward Tsang, Foundations of Constraint Satisfaction, Academic Press, 1993  ISBN 0-12-701610-4
• (en) Rina Dechter, Constraint processing, Morgan Kaufmann, 2003  ISBN 1-55860-890-7
• (en) Krzysztof Apt, Principles of constraint programming, Cambridge University Press, 2003  ISBN 0-521-82583-0
• (en) Christophe Lecoutre, Constraint Networks: Techniques and Algorithms, ISTE/Wiley, 2009  ISBN 978-1-84821-106-3
• (en) Tomás Feder, Constraint satisfaction: a personal perspective, manuscript.
• (en) Constraints archive
• (en) CSPLib : a problem library for constraints
• (en) Forced Satisfiable CSP Benchmarks of Model RB
• (en) Benchmarks -- XML representation of CSP instances