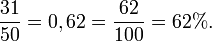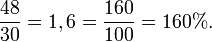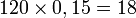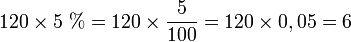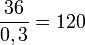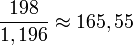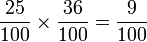Pourcentages

Un pourcentage est une façon d'exprimer un nombre comme une fraction de cent, généralement en utilisant le signe %, parfois l'abréviation p.c., ou rarement en écrivant en toutes lettres pour cent : 5 %, 5 p.c., 5 pour cent. On utilise le pourcentage seulement lorsqu'un nombre représente une proportion ou une fraction d'un ensemble.

D'usage très fréquent dans le monde actuel puisqu'on le rencontre en statistique comme en économie, le pourcentage est une notion qui peut induire de nombreuses erreurs de raisonnement.

Sommaire 1 Notation 2 Calculs élémentaires 2.1 Calculer un pourcentage 2.2 Appliquer un pourcentage 2.3 Retrouver la valeur de référence (pourcentage « indirect ») 2.4 Pourcentage d'augmentation et de réduction 2.4.1 Calculer la valeur finale 2.4.2 Coefficients multiplicateur ou diviseur et pourcentages 2.4.3 Retrouver la valeur de référence (pourcentage "indirect") 2.5 Pourcentage de pourcentage 3 Pourcentages courants 4 Usage des pourcentages 4.1 Statistique 4.2 Domaine économique ou financier 4.3 Topographie 4.4 Métrologie 4.5 Œnologie 5 Dangers et pièges 5.1 Le pourcentage n'est pas une quantité 5.2 L'importance de l'univers de référence 5.3 Pourcentage et point 5.4 Pourcentage composé 6 Voir aussi 6.1 Articles connexes 6.2 Bibliographie 6.3 Liens externes 7 Notes et références

Notation

La notation des pourcentages semble tirer son origine de l'italien. Dans les textes du Moyen Âge, on peut voir des notations comme « per cento ». ou « per c. » ou « p. cento ». Selon D.E Smith^[1], la première trace d'un symbole voisin de celui utilisé actuellement, se trouve dans un manuscrit italien anonyme écrit vers 1425 sous la forme 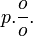Le p s'est ensuite perdu et la barre est devenue oblique. Les deux « o » ont ensuite été assimilés aux deux zéros de 100 ce qui a conduit à noter ‰ le symbole « pour mille ».

Le signe « % » en typographie française doit être précédé et suivi d'une espace forte^[2],[3].

Dans d'autres langues, et notamment en anglais, le signe est collé au chiffre.

Calculs élémentaires

On compare une valeur particulière à une valeur de référence, et on cherche à déterminer ce que vaudrait cette valeur particulière si la valeur de référence était ramenée à 100 tout en respectant les proportions.

Avec un vocabulaire de statistique descriptive, on peut écrire qu'on compare une population partielle à une population totale, et qu'on cherche à déterminer ce que vaudrait cette population partielle si la population totale était ramenée à 100 tout en respectant les proportions.

Exemple : 56 personnes parmi 400 (population de référence) ont une particularité P. Donc 14 % ont une particularité P. En effet, pour ramener 400 à 100, il faut diviser 400 par 4, et faire de même avec 56 pour conserver la proportion. Or 56 / 4 = 14.

Le calcul de ce pourcentage revient à trouver le numérateur d'une fraction dont le dénominateur serait 100 et qui serait égale à 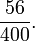C'est ainsi que l'on confond souvent la fraction de dénominateur 100 avec le pourcentage et donc le pourcentage avec le nombre décimal 0,14. Cette confusion, très pratique en mathématique, induit parfois des incompréhensions dans le domaine technique puisque l'on rencontre souvent l'indication de calcul suivante : pourcentage de personne ayant la particularité P :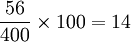

Calculer un pourcentage

Dans une assemblée de 50 personnes, il y a 31 femmes. Celles-ci représentent 62 % de l'assemblée car :

On peut aussi voir le problème comme la recherche d'une quatrième proportionnelle. Il s'agit de trouver t tel que :

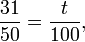soit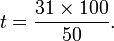

Quand on compare une valeur particulière à une valeur de référence, il est possible d'obtenir des pourcentages dépassant 100 %. Si le coût d'un produit passe de 30 euros à 48 euros et si on considère que le premier prix est une valeur de référence, le second prix représente 160 % du premier prix car :

Cet aspect du pourcentage est particulièrement utilisé en économie dans la notion d'indice.

Appliquer un pourcentage

Appliquer un pourcentage, c'est retrouver la valeur étudiée (ou la population partielle) connaissant le pourcentage et la valeur (ou la population) de référence. Cette valeur étudiée se détermine en multipliant la valeur de référence par le décimal associé au pourcentage.

Si une assemblée de 120 personnes compte 15 % de femmes, alors il y a 18 femmes dans cette assemblée car :

On peut aussi voir le problème comme la recherche d'une quatrième proportionnelle : il faut trouver n tel que :

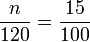ce qui conduit à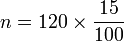

Le prix hors taxes d'un objet est 120 €. Le taux de TVA est de 5 %. Celle-ci s'élève donc à 6 € car :

Retrouver la valeur de référence (pourcentage « indirect »)

Cette valeur de référence se trouve en divisant la valeur étudiée ou la population partielle par le décimal associé au pourcentage.

Dans une assemblée il y a 36 femmes, elles représentent 30 % de l'assemblée donc l'assemblée est formée de 120 individus car :

On peut aussi voir le problème comme la recherche d'une quatrième proportionnelle : il faut trouver N tel que :

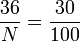soit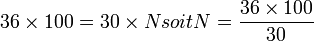

Le prix TTC d'un objet est de 198 €. Ce prix représente 119,6 % du prix HT. Le prix HT (hors taxe) est donc de 165,55 € car

Pourcentage d'augmentation et de réduction

En économie et dans les taux d'intérêts, l'étude porte sur des variations en pourcentage, des augmentations ou des réductions. On peut tout à fait décomposer le calcul en deux temps : calcul de l'augmentation ou de la réduction, puis calcul de la valeur finale en effectuant une addition ou une soustraction. Mais il est préférable de voir ces augmentations ou ses réductions comme issues de l'application d'un coefficient multiplicateur. Seul cet aspect des choses permet de retrouver efficacement une valeur de référence ou d'appliquer des augmentations successives.

Calculer la valeur finale

Une augmentation de t % se traduit par une multiplication par 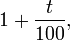et une diminution de t % par une multiplication par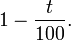

Des variations successives à taux fixe conduisent à des progressions géométriques. Ainsi, augmenter 35 fois de 2 % revient à multiplier par 1,02³⁵, c'est-à-dire 1,99989, soit quasiment par 2. Et diminuer 35 fois de 2 % revient à multiplier par 0,98³⁵, c'est-à-dire à diviser par 2,028, soit un peu plus de 2.

Coefficients multiplicateur ou diviseur et pourcentages

Si un prix par exemple a été multiplié par un coefficient C ceci correspond à une augmentation de t % telle que 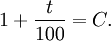Soit 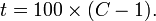De telle sorte que si un prix a été multiplié par 8 en 10 ans cela correspond à une augmentation de 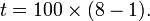soit une augmentation de 700 % en 10 ans et non pas 800 % comme on pourrait le croire. De même un prix multiplié par 2 correspond à une hausse de 100 %.

Pour une baisse, si un prix a été divisé par un coefficient D ceci correspond à une baisse de t % telle que 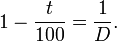soit encore 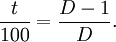d'où 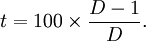Ainsi, si un prix a été divisé par 2 cela correspond à une baisse de 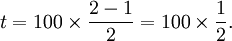soit 50 %. Pour un prix divisé par 4 la baisse est de 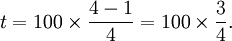soit 75 %.

Retrouver la valeur de référence (pourcentage "indirect")

Pour retrouver la valeur de référence, il suffit alors de diviser la valeur finale par le coefficient multiplicateur.

Après une remise de 15 % le prix d'un objet n'est plus que de 34 €, le prix initial de l'objet était donc de 40 € car :

la réduction correspond à une multiplication par 1 - 0,15 = 0,85

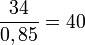
Pourcentage de pourcentage

On peut être amené à multiplier entre eux des pourcentages. C'est le cas par exemple des pourcentages de pourcentage. Dans cette assemblée, il y a 36 % de femmes et 25 % de ces femmes sont âgées de plus de 50 ans. Il y a donc 9 % de femmes âgées de plus de 50 ans dans l'assemblée car :

On peut voir le problème en se ramenant à une assemblée de 100 personnes. Parmi celles-ci 36 seraient des femmes et 25 % de ces 36 femmes seraient âgées de plus de 50 ans. Or 25 % de 36 correspond à 9 donc dans une assemblée de 100 personnes, il y aurait 9 femmes de plus de cinquante ans.

Pourcentages courants

Notation en
français	fraction	décimal	pour-cent
un millième	1/1000	0,001	0,1 %
un centième	1/100	0,01	1 %
un dixième	1/10	0,1	10 %
un cinquième	1/5	0,2	20 %
un quart	1/4	0,25	25 %
un tiers	1/3	0,33…	33,3… %
une moitié	1/2	0,5	50 %
deux tiers	2/3	0,66…	66,6… %
trois quarts	3/4	0,75	75 %
neuf dixièmes	9/10	0,9	90 %
99 centièmes	99/100	0,99	99 %
999 millièmes	999/1000	0,999	99,9 %
le tout	1/1	1	100 %
le double	2/1	2	200 %

Usage des pourcentages

Statistique

En statistique, quand on étudie une variable statistique, les effectifs associés aux différentes valeurs du caractère sont parfois difficiles à bien évaluer. Se ramener alors a une population de 100, revient à présenter des répartitions sous formes de pourcentage. On parle alors de fréquence.

On rencontre les pourcentages dans les sondages d'opinion alors que la population interrogée est rarement de 100 personnes. On les rencontre aussi dans les résultats d'élections.

Domaine économique ou financier

Dans les finances, on rencontre les pourcentages dans les calculs de TVA : une TVA de 19,6 % consiste à ajouter à un prix hors taxes (prix HT) une taxe correspondant à 19,6 % du prix HT. On obtient alors un prix toutes taxes comprises (prix TTC) qui correspond au prix HT multiplié par 1,196.

On les rencontre aussi dans les taux d'intérêts : une somme placée ou empruntée pendant un an à un taux d'intérêt de t % a été multipliée en fin d'année par .

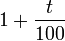Les taux d'imposition qui représentent une fraction du revenu d'un ménage sont aussi exprimés sous forme de pourcentage.

En économie, un indice est la valeur d'une grandeur économique par rapport à une valeur de référence. Par exemple, si, en 2004, le prix moyen des appartements au mètre carré dans une ville a augmenté de 22 % par rapport à l'année 2000, servant de référence (indice 100), on dira que l'indice du prix moyen des appartements est de 122 en 2004. L'indice est donc une présentation particulière d'un pourcentage.

Topographie

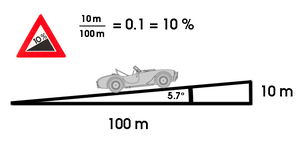
Les panneaux routiers indiquent les pentes des routes en pourcentage. Une pente de 10 % signifie qu'à un déplacement horizontal de 100 m, correspond un déplacement vertical de 10 m. La pente correspond alors à la tangente de l'angle d'inclinaison de la route.

Métrologie

En métrologie, les mesures ne peuvent pas être connues avec une précision absolue. Les calculs d'erreur ou les calculs d'incertitude sont souvent présentés en pourcentage. Quand on dit que le poids d'une conserve est connu à 5 % près, cela signifie que, si le poids de la conserve est supposé valoir 500 grammes, il peut se glisser une erreur de 25 grammes en excès ou en défaut.

Œnologie

En œnologie, le degré alcoolique d'une boisson alcoolisée est le pourcentage en volume d'alcool pur contenu dans une boisson. Ainsi, si on prend un verre de 100 ml de vin titré à 12 % vol, on absorbe 12 ml d'alcool pur soit environ 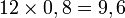grammes d'alcool pur.

Le terme de degré pris à la place de pourcentage provient de l'ancienne unité utilisée : le degré Gay-Lussac (GL). Un degré GL correspondant à un pourcentage d'alcool pur de 1 %.

Dangers et pièges

L'importance des pourcentages dans l'analyse des données statistiques, leur présence dans les résultats de sondages et dans les indicateurs économiques leur confèrent un statut officiel de science. Cependant, le pourcentage est une vision réductrice d'une réalité et son usage abusif pour conduire à des erreurs de raisonnement que Sylviane Gasquet souligne dans son livre Plus vite que son nombre.

Le pourcentage n'est pas une quantité

La représentation du pourcentage sous forme d'une fraction, sa transformation en décimal, lui confère un statut apparent de nombre mais il n'a pas les qualités normalement attribuées à un nombre : il n'est pas possible d'effectuer des sommes de pourcentage dans l'absolu. On ne peut pas faire de sommes de pourcentage et leur donner un sens, sauf si ces pourcentages correspondent à deux populations partielles disjointes associées à la même population de référence. En particulier deux augmentations successives de 10 % ne donnent pas une augmentation de 20 % mais de 21 %. Quant au produit de pourcentage, il obéit à des règles très restrictives. De même, comparer des pourcentages peut se révéler mener à des contresens si la population de référence change dans les deux comparaisons.

L'importance de l'univers de référence

Le fait de ramener l'effectif à 100 tend à donner moins d'importance à la population de référence qui parfois même disparaît du discours final. Cela peut induire un certain nombre de contresens.

Deux phénomènes peuvent contribuer à l'augmentation d'un pourcentage  : l'augmentation de la population partielle, la diminution de la population totale.

Un mauvais choix de l'univers de référence induit le lecteur à une mauvaise interprétation du pourcentage. Sylviane Gasquet cite l'exemple du redoublement en seconde : dans l'expression, il y a 50 % de redoublement en seconde, l'univers de référence a disparu. Il faudrait dire, dans une classe de seconde, 50 % des élèves sont amenés à redoubler. Comme la moitié de la classe est déjà formée de redoublants qui, on l'espère ne vont pas tripler, c'est que 100 % des non-redoublants sont condamnés à redoubler.

Un taux de TVA s'applique au prix hors taxe et non au prix TTC.

Pourcentage et point

Quand une population partielle est passée de 10 % à 12 %, il est délicat de parler de l'augmentation. Une erreur fréquente est de dire que la population a augmenté de 2 %. En effet, en supposant que la population de référence soit de 100 individus et ne change pas entre la première et la seconde mesure (ce qui est rarement le cas), la population partielle passerait de 10 individus à 12 individus, soit une multiplication par 1,2 c'est-à-dire une augmentation de 20 %. Or pourtant, il est utile de chiffrer cette variation : premier pourcentage 10 %, second 12 %. On parle alors d'une augmentation de 2 points.

Pourcentage composé

Lors de hausses et de baisses successives, la tentation est grande d'ajouter et soustraire les pourcentages d'augmentation.

Il est tentant de penser qu'une augmentation de 10 % suivie d'une baisse de 10 % ramène à la valeur initiale. Mais ces pourcentages ne correspondent pas à la même population de référence. En reprenant la technique du coefficient multiplicatif et l'appliquant à une quantité Q on s'aperçoit que les 10 % d'augmentation reviennent à multiplier la quantité Q par 1,1 et que la réduction, s'appliquant à 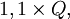revient à multiplier cette quantité par 0,9. Or 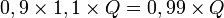ce qui correspond à une baisse de 1 %.

Voir aussi

Articles connexes

• Pourmille
• Partie par million
• Per unit
• TCAM

Bibliographie

• Sylviane Gasquet-More, Plus vite que son nombre, éditions du seuil, (ISBN 2-02-034563-3)

Liens externes

• Pour apprendre sans peine
• Représenter facilement des pourcentages

Notes et références