- Per unit
-
Unité réduite
En physique et en ingénierie, une unité réduite ou per unit (abréviation pu) est une unité sans dimension pouvant mesurer n'importe quelle grandeur physique, pourvu qu'elle ait été définie avant son usage.
Quelle que soit la grandeur physique considérée, le per unit la mesurant se rapporte à une échelle de référence en unité physique réelle qui doit être explicitée. Cette échelle de référence est normalement choisie, pour chaque unité physique intervenant dans le problème, de telle sorte que toutes les valeurs effectives soient aux alentours de 1 pu.
Sommaire
Avantages et inconvénients
Le principal avantage est de pouvoir comparer rapidement des résultats numériques avec le système de référence, car le cerveau humain est plus à l'aise avec des quantités proches de 1 qu'avec des très grands ou très petits nombres.
D'autre part, contrairement au pourcent, utilisé pour les mêmes raisons, le per unit se conserve dans les opérations de multiplication et division, et donc permet de définir un système d'unités complet et cohérent.
Le principal inconvénient est que toute analyse dimensionnelle devient impossible.
Usages courants
Électrotechnique
Les électrotechniciens font souvent leurs calculs en pu. Pour cela, on commence par se définir la tension nominale (Vn), le courant nominal (In), et la fréquence nominale (fn) si l'on est en alternatif, du système. Tous les calculs suivants se font en pu (base Vn, In, fn), par exemple :
- La puissance nominale est pn=in*vn=1*1=1pu par définition ;
- Un transformateur de puissance 0.93pu a une puissance réelle de 0,93*Pn=0,93*Vn*In ;
- L'inductance vaut 0,1 pu signifie que son impédance vaut 0,1*Vn/In (Zn=Vn/In est l'impédance de référence) ;
- etc.
Astronomie
Les astronomes se définissent souvent des unités pratiques dans un certain contexte.
Par exemple, l'unité astronomique est une unité réduite (l'une des rares à avoir un nom distinctif) ayant pour référence le demi-grand axe de l'orbite terrestre (environ 150 millions de km). Elle mesure donc des longueurs, et sera utile pour des mesures sur des systèmes dont la taille est de l'ordre de grandeur de celle du système solaire.
De même, lorsqu'on donne la masse d'une étoile en nombre de masses solaires, ou celle d'une planète en nombre de masses joviennes ou terrestres, on utilise des unités réduites.
Physique quantique
La physique quantique définit des unités naturelles telles que la longueur de Planck et le temps de Planck, qui servent parfois d'échelle de référence à des unités réduites.
En physique atomique et en chimie, donc en électrodynamique quantique (QED : quantum electrodynamics), la base du système d'unités atomiques se compose de :
- la masse m de l'électron (9.10-31 kg) ;
- la constante de Planck réduite : ℏ = 1.10-34 J.s ;
- la constante
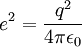, q étant la charge de l'électron en coulombs (1,6 10-19 C).
Généralisation : système d'unités naturelles
Tout système d'équations possède SON propre système d'unités naturelles. Dans ce système, il est très fréquent que les ordres de grandeur soient de l'ordre de 1. Si cela n'est pas le cas, un physicien doit en chercher la cause profonde (règle de Wheeler : cf Ordre de grandeur)
Voir aussi
- Analyse dimensionnelle
- Nombres sans dimension
- Pourcentage
- système d'unités atomiques
- système d'unités naturelles
Portail de la physique
Catégories : Physique | Unité de mesure naturelle
Wikimedia Foundation. 2010.
