Rho algorithme

En analyse numérique, le ρ-algorithme est un algorithme non linéaire d'accélération de la convergence d'une suite numérique dû à Peter Wynn^[1]. C'est un algorithme analogue à l'extrapolation de Richardson, mais basé sur une extrapolation par fraction rationnelle au lieu d'une extrapolation polynomiale. Il est particulièrement bien adapté à accélérer les suites à convergence logarithmiques.

Description de l'algorithme

Le ρ-algorithme consiste à calculer une fraction rationnelle d'interpolation à l'aide des valeurs connues de la suite, et de déterminer la limite en l'infini de cette fraction comme une estimation de la limite de la suite numérique. Il utilise pour cela les différences réciproques, qui fournissent directement le résultat cherché. L'algorithme obtenu se résume donc au calcul des différences réciproques de la suite numérique.

Soit une suite numérique S_n dont on cherche à connaître la limite S. le ρ-algorithme consiste à calculer un tableau en initialisant la première colonne par la suite S_n, et en calculant les autres cases à l'aide des relations suivantes :

$\rho^{(n)}_{-1}=0 \text{ } \rho^{(n)}_{0}=S_n \text{ }\forall n$

$\rho^{(n)}_{k+1}= \rho^{(n+1)}_{k-1} + \frac{k+1}{\rho^{(n+1)}_{k} - \rho^{(n)}_{k}} \text{ }\forall n,k$

Les différentes colonnes d'indice k paires du tableau fournissent d'autres suites convergeant en général plus vite que la suite S_n d'origine. Les colonnes d'indice impaires peuvent êtres considérés comme des intermédiaires de calcul.

On présente souvent les résultats du ρ-algorithme sous forme d'un tableau aux lignes décalées : la formule de calcul du ρ-algorithme relie ainsi les termes formant un losange dans le tableau.

$\begin{matrix} 0 & & & & & \\ & \rho^{(0)}_{0}=S_0 & & & & \\ 0 & & \rho^{(0)}_{1} & & & \\ & \rho^{(1)}_{0}=S_1 & & \rho^{(0)}_{2} & & \\ 0 & & \rho^{(1)}_{1} & & \rho^{(0)}_{3} & \\ & \rho^{(2)}_{0}=S_2 & & \rho^{(1)}_{2} & & \rho^{(0)}_{4} \\ 0 & & \rho^{(2)}_{1} & & \rho^{(1)}_{3} & \cdots \\ & \rho^{(3)}_{0}=S_3 & & \rho^{(2)}_{2} & & \rho^{(1)}_{4} \cdots \\ & \vdots & & \vdots & & \vdots \\ \end{matrix}$

Il arrive fréquemment que la suite à accélérer S_n dépende d'une suite auxiliaire x_n, celle-ci tendant vers l'infini (par exemple des approximations par discrétisation avec un maillage de plus en plus fin, où x_n serait le nombre de mailles). Il est possible d'utiliser le ρ-algorithme de base dans ces cas mais la façon dont évolue la suite x_n associée (par exemple l'évolution du nombre de mailles entre chaque S_n) est un renseignement précieux qui pourrait aider l'accélération de la convergence. On utilise dans ce cas une généralisation du ρ-algorithme utilisant cet information supplémentaire: il correspond à la limite en l'infini de la fraction rationnelle d'interpolation, passant par les points (x_n, S_n).

$\rho^{(n)}_{-1}=0 \text{ } \rho^{(n)}_{0}=S_n \text{ }\forall n$

$\rho^{(n)}_{k+1}= \rho^{(n+1)}_{k-1} + \frac{x_{n+k+1}-x_{n}}{\rho^{(n+1)}_{k} - \rho^{(n)}_{k}} \text{ }\forall n,k$

Avec la suite auxiliaire x_n=n, on retrouve le ρ-algorithme classique.

Propriétés

Lien avec la formule de Thiele

La formule de Thiele^[2] est une méthode de calcul de fraction rationnelle d'interpolation s'apparentant à celle de Newton pour les polynômes d'interpolation. La fraction rationnelle de Thiele passant par les points (x_i, S_i) pour i=n, n+1...n+k se présente sous forme d'une fraction continue qui s'écrit:

$T^{(n)}_{k}(x) = \rho^{(n)}_{0} + \cfrac {x-x_n}{\rho^{(n)}_{1}-\rho^{(n)}_{-1} + \cfrac {x-x_{n+1}} {\rho^{(n)}_{2}-\rho^{(n)}_{0} + \cfrac {x-x_{n+2}} {\rho^{(n)}_{3}-\rho^{(n)}_{1}+ \cfrac {x-x_{n+3}} {\rho^{(n)}_{4}-\rho^{(n)}_{2}+\cdots+\cfrac {...} {\rho^{(n)}_{k-1}-\rho^{(n)}_{k-3}+\cfrac {x-x_{n+k-1}} {\rho^{(n)}_{k}-\rho^{(n)}_{k-2}}}}}}}$

soit, pour tous les points à partir de (x₀, S₀)

$S(x) = \rho^{(0)}_{0} + \cfrac {x-x_0}{\rho^{(0)}_{1}-\rho^{(0)}_{-1} + \cfrac {x-x_1} {\rho^{(0)}_{2}-\rho^{(0)}_{0} + \cfrac {x-x_2} {\rho^{(0)}_{3}-\rho^{(0)}_{1}+ \cfrac {x-x_3} {\rho^{(0)}_{4}-\rho^{(0)}_{2}+\cdots}}}}$

où les différences divisées ρ⁽ⁿ⁾_k sont calculées avec la suite S_i et la suite auxiliaire x_i. La fonction de Thiele est une fraction rationnelle de degrés identiques au numérateur et dénominateur pour k pair et de degré supérieur de 1 au numérateur pour k impair. Plus précisément, on a:

$T^{(0)}_{2k}(x)=\frac{\rho^{(0)}_{2k} x^k+...}{x^k+...}$

$T^{(0)}_{2k+1}(x)=\frac{x^{k+1}+...}{\rho^{(0)}_{2k+1} x^k+...}$

On en déduit facilement que, lorsque k est pair, le ρ-algorithme correspond à la limite en l'infini de la fraction d'interpolation de Thiele. De plus, on peut en déduire aussi que les différences réciproques ρ⁽ⁿ⁾_k ne dépendent pas de l'ordre des points ayant servi à les calculer (puisque la fraction d'interpolation ne dépends pas de cet ordre et que la différence réciproque est un des coefficients de cette fraction).

Exemples

Accélération de la convergence d'une suite numérique

La série suivante, série dite du problème de Bâle,

$\sum_{n=1}^\infin \frac{1}{n^2} = \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \cdots = \frac{ \pi^2} {6}=1,64493406684822643...$

converge très lentement. Le ρ-algorithme peut être utilisé pour accélérer la convergence des sommes partielles de cette série. Voici le résultat :

$\scriptstyle{\begin{matrix} & \rho^{(n)}_{0}=S_n & & \rho^{(n)}_{2} & & \rho^{(n)}_{4} & & \rho^{(n)}_{6} & & \rho^{(n)}_{8 } \\ 0 & & & & & & & \\ & 1 & & & & & & \\ 0 & & 4 & & & & & \\ & 1,25 & & 1,65 & & & & \\ 0 & & 9 & & -936 & & \\ & 1,3611111 & & 1,64682540 & & 1,64489489 & & \\ 0 & & 16 & & -3008 & & 177552,00 \\ & 1,42361111 & & 1,64583333 & & 1,64492259 & & 1,64493438 \\ 0 & & 25 & & -7400 & & 686475,00 & & -29649576,9 \\ & 1,46361111 & & 1,64542929 & & 1,64492979 & & 1,64493438 & & 1,644934064 \\ 0 & & 36 & & -15408 & & 2064852,04 & & -128422187,3 \\ & 1,49138889 & & 1,64523504 & & 1,64493220 & & 1,64493415 \\ 0 & & 49 & & -28616 & & 5229818,72 \\ & 1,51179705 & & 1,64523504 & & 1,64493315 \\ 0 & & 64 & & -48896 \\ & 1,52742205 & & 1,64513039 \\ 0 & & 81 \\ & 1,53976773 \\ \end{matrix}}$

Le ρ-algorithme classique a été utilisée pour les calculs précédents. La suite à accélérer est la somme partielle de la série, en ajoutant un terme à la fois. On constate effectivement que seules les colonnes paires convergent vers la limite, et ceci beaucoup plus vite que la suite d'origine (pour obtenir la même précision avec la suite d'origine, il aurait fallu sommer plusieurs milliards de termes au lieu de 9).

Interpolation rationnelle

Comparaison de l'interpolation polynomiale et rationnelle de la fonction Arctan(x)

Le calcul des différences réciproques (tableau de valeur du ρ-algorithme) permet d'utiliser la formule de Thiele pour le calcul de fraction rationnelle d'interpolation. L'interpolation rationnelle fournit de meilleurs résultats par rapport à l'interpolation polynomiale, lorsque la fonction à interpoler :

– présente des asymptotes ;

– présente des pôles à proximité ou dans la zone d'interpolation ;

– présente des pôles complexes au voisinage de l'intervalle d'interpolation (phénomène de Runge).

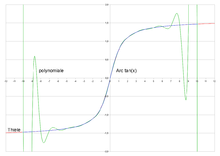
Le graphique ci contre montre le gain que peut apporter l'interpolation rationnelle sur l'interpolation polynomiale dans certains cas. L'exemple porte sur l'interpolation de la fonction Arc-tangente à l'aide de 21 points d'interpolation régulièrement espacés sur l'intervalle [-10;10]. On constate que l'interpolation polynomiale présente un phénomène de Runge. L'interpolation rationnelle est quasiment confondue avec la fonction arc tangente dans l'intervalle d'interpolation, et même légèrement au delà. La fonction Arc-tangente présente des asymptotes horizontales et des pôles complexes en -i et +i, conditions non favorables pour une interpolation polynomiale. Le phénomène de Runge peut être estompé en resserrant les abscisses d'interpolation aux extrémités de l'intervalle, par exemple avec les abscisses de Chebychev: cependant l'amélioration obtenue ne suffit pas à tenir la comparaison avec l'interpolation rationnelle (erreur max de l'ordre de 0,07 contre 0,00005).

Variante des méthodes utilisant l'extrapolation de Richardson

Plusieurs méthodes numériques utilisent l'extrapolation de Richardson pour accélérer la convergence de méthodes d'ordre peu élevé. On trouve par exemple son utilisation dans:

– l'évaluation de la dérivée d'une fonction, par accélération de la convergence de la méthode des différences centrales ;

– l'intégration numérique, en accélérant la méthode des trapèzes (méthode de Romberg) ;

– l'intégration des équation différentielles, en accélérant la méthode du point milieu (méthode de Gragg-Bulirsch-Stoer).

Dans chacune de ces applications, il est possible de remplacer l'extrapolation de Richardson par le ρ-algorithme. La suite associée x_n devant tendre vers l'infini dans le cas du ρ-algorithme, on prendra l'inverse de la suite associée à l'extrapolation de Richardson (ou leur carré, le cas échéant). Les colonnes impaires de l'algorithme ne convergeant pas vers la limite cherchée, la valeur à retenir pour l'extrapolation est alternativement ρ⁽⁰⁾_k pour k pair et ρ⁽¹⁾_k-1 pour k impair. Bulirsch et Stoer^[3] ont proposé dans ce but une autre méthode d'interpolation rationnelle qui, pour un nombre paire de points, donne les mêmes résultats que le ρ-algorithme, mais nécessite plus de calculs.

Autres applications

Le ρ-algorithme s'est révélé intéressant pour divers applications pratiques, entre autres :

– l'inversion numérique de la transformation de Laplace^[4];

– l'accélération de la convergence d'algorithmes de restauration d'images (algorithme de Richardson-Lucy).

Notes

↑ Wynn, « On a procrustean technique for the numerical transformation of slowly convergent sequences and series », dans Mathematical Proceedings of the Cambridge Philosophical Society, vol. 52, 1956, p. 663–671 [lien DOI]
↑ Thiele, T. N. : Interpolationsrechnung. Leipzig: Teubner 1909
↑ Bulirsch, R, Stoer, J.:Numerical treatment of ordinary differential equations by extrapolation methods. Numer. Math. 8, 1-13 (1966)
↑ Multi-precision Laplace transform inversion, J. Abate et P. P. Valkó, http://www.pe.tamu.edu/valko/public_html/CV/ValkoPDF/2004AV_IJNME_Multi.pdf

Références

Claude Brezinski, Algorithmes d'accélération de la convergence: étude numérique, éditions Technip, 1978, (ISBN 2-7108-0341-0)

Voir aussi

Articles connexes

Portail de l'analyse

Catégorie :

Analyse numérique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Rho algorithme de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires: