Pendule de bessel

Pendule de bessel: Pendule de Bessel

Le pendule simple de longueur variable

Quand la longueur d'un pendule simple varie de manière affine: l(t)= lo + vt, on dit qu'il s'agit d'un pendule de Bessel, car la solution (pour de petites oscillations) s'exprime à l'aide des fonctions de Bessel. Si v est faible, on retrouve l'invariant adiabatique E(t)T(t) (voir pendule adiabatique).

Sommaire

1 Équation du pendule de longueur variable

2 Équation de Bessel

3 Résolution avec les conditions initiales

4 Voir aussi

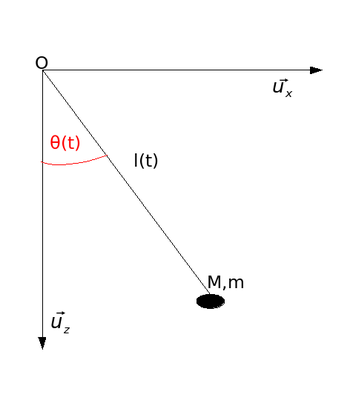
Équation du pendule de longueur variable

Le pendule simple de longueur variable a pour équation pour cette loi temporelle de l(t) où sa dérivée seconde est nulle:

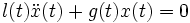
$l(t) \ddot{x} (t) + g(t) x(t) = 0$

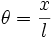Dans le cas habituel g est constant. Revenons à la fonction angulaire $\theta= \frac xl$ :

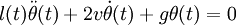
$l(t) \ddot{\theta}(t) +2v \dot{\theta}(t) + g \theta(t) =0$

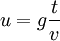Posons comme nouvelle variable sans unités $u = g \frac tv$ :

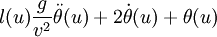
$l(u) \frac g{v^2} \ddot{\theta}(u) +2 \dot{\theta} (u)+ \theta (u)$

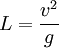Puis pour simplifier, posons comme longueur $L= \frac {v^2}{g}$ :

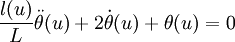
$\frac{l(u)}{L} \ddot{\theta} (u) + 2 \dot{\theta} (u)+ \theta (u)= 0$

On reconnait l'équation circuit RLC avec self variable linéairement, c'est un problème classique (voir obtention de champs magnétiques intenses). On peut encore transformer cette équation.

Équation de Bessel

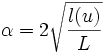On fait un nouveau changement de variable sans unités $\alpha= 2 \sqrt { \frac {l(u)}{L}}$ :

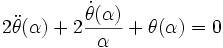
$2 \ddot{\theta} (\alpha) +2 \frac {\dot {\theta} (\alpha)}{\alpha}+\theta(\alpha)=0$

On change de fonction $y (α) = αθ(α)$ , et on finit par trouver une équation de Bessel avec n=1:

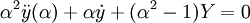
$\alpha^2 \ddot{y} (\alpha)+\alpha \dot{y} + (\alpha^2-1)Y = 0$

Les solutions sont les fonctions de Bessel, fonctions classiques de la physique mathématique (cf Campbell, par exemple):

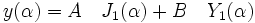
$y(\alpha)=A \quad J_1(\alpha)+B \quad Y_1(\alpha)$

D'où: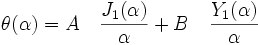 $\theta(\alpha)=A \quad \frac {J_1(\alpha)}{\alpha}+B \quad \frac {Y_1(\alpha)}{\alpha}$

Résolution avec les conditions initiales

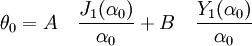
$\theta_0= A \quad \frac {J_1(\alpha_0)}{\alpha_0}+B \quad \frac {Y_1(\alpha_0)}{\alpha_0}$

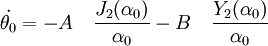
$\dot{\theta_0}= -A \quad \frac {J_2(\alpha_0)}{\alpha_0}-B \quad \frac {Y_2(\alpha_0)}{\alpha_0}$

On résout ce système linéaire de deux équations à deux inconnues et qui donne finalement :

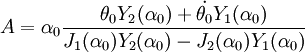
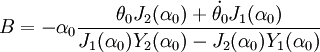
$A = \alpha_0 \frac {\theta_0 Y_2(\alpha_0)+ \dot{\theta_0} Y_1(\alpha_0)}{J_1(\alpha_0)Y_2(\alpha_0)-J_2(\alpha_0)Y_1(\alpha_0)}$ $B =-\alpha_0 \frac {\theta_0 J_2(\alpha_0)+ \dot{\theta_0} J_1(\alpha_0)}{J_1(\alpha_0)Y_2(\alpha_0)-J_2(\alpha_0)Y_1(\alpha_0)}$

On peut alors tracer $θ(t)$ à l'aide d'un logiciel.

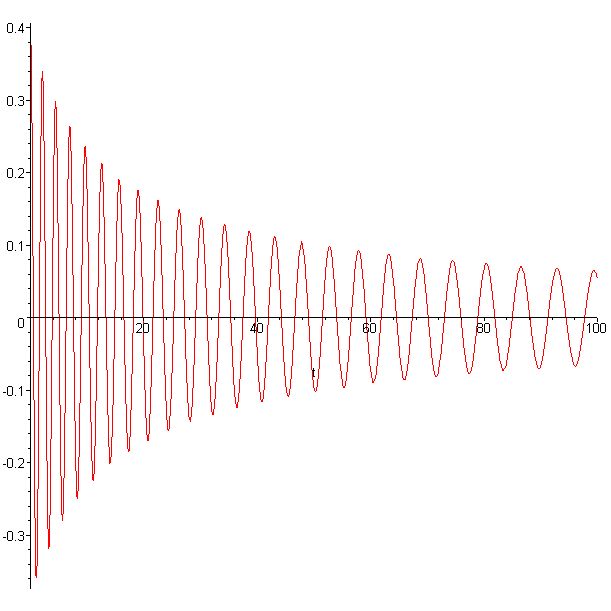
On peut même vérifier graphiquement, que si v est faible, E(t)T(t) est une constante (pendule adiabatique). Il faut néanmoins se rappeler qu'on s'est toujours placé dans le cas des petites oscillations. Bien sûr, n'importe quelle méthode numérique type Runge-Kutta donne les mêmes résultats sans obtenir la formule générale.

Voir aussi

pendule de longueur variable

pendule adiabatique

Portail de la physique

Ce document provient de « Pendule de Bessel ».

Catégorie : Pendule

Contenu soumis à la licence CC-BY-SA. Source : Article Pendule de bessel de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

Pendule de Bessel — Le pendule simple de longueur variable Quand la longueur d un pendule simple varie de manière affine: l(t)= lo + vt, on dit qu il s agit d un pendule de Bessel, car la solution (pour de petites oscillations) s exprime à l aide des fonctions de… … Wikipédia en Français
Pendule de longueur variable — Pendule simple de longueur variable La charge soulevée par une grue est un pendule simple de longueur variable l(t). En considérant simplement les petites oscillations, pour raison de simplicité, on peut montrer que descendre la masse réduit l… … Wikipédia en Français
Pendule simple — Schéma montrant un pendule simple. En physique, le pendule simple est une masse ponctuelle fixée à l extrémité d un fil sans masse, inextensible et sans raideur[1] et oscillant sous l effet de la pesanteur. Il s agit du modèle de pen … Wikipédia en Français
Pendule simple de longueur variable — Le pendule simple de longueur variable modélise une charge soulevée par une grue. Quand la longueur se raccourcit, l amplitude des oscillations augmente et la puissance du moteur de la grue ne se réduit plus à lutter contre la pesanteur. Sommaire … Wikipédia en Français
Pendule adiabatique — On appelle équation du pendule adiabatique l équation différentielle : . lorsque la pulsation ω varie lentement; on dit alors qu il y a adiabatisme mécanique. L analyse WKB conduit à la remarquable conclusion qu il existe un invariant… … Wikipédia en Français
Fonction de Bessel — En mathématiques, et plus précisément en analyse, les fonctions de Bessel, découvertes par le mathématicien suisse Daniel Bernoulli, portent le nom du mathématicien allemand Friedrich Bessel. Bessel développa l analyse de ces fonctions en 1817… … Wikipédia en Français
Fonction De Bessel — Les fonctions de Bessel, découvertes par le mathématicien suisse Daniel Bernoulli, portent le nom de Friedrich Bessel, et sont des solutions y de l équation différentielle de Bessel : pour tout nombre réel ou complexe n. Le cas le plus… … Wikipédia en Français
Fonction de bessel — Les fonctions de Bessel, découvertes par le mathématicien suisse Daniel Bernoulli, portent le nom de Friedrich Bessel, et sont des solutions y de l équation différentielle de Bessel : pour tout nombre réel ou complexe n. Le cas le plus… … Wikipédia en Français
Fonctions de Bessel — Fonction de Bessel Les fonctions de Bessel, découvertes par le mathématicien suisse Daniel Bernoulli, portent le nom de Friedrich Bessel, et sont des solutions y de l équation différentielle de Bessel : pour tout nombre réel ou complexe n.… … Wikipédia en Français
De L'ellipsoïde Au Géoïde — Cet article décrit sommairement les progrès de la géodésie dans le cadre plus large des sciences physiques au cours du XIXe et de la première moitié du XXe siècle, jusqu à l arrivée des satellites artificiels et la naissance de la géodésie… … Wikipédia en Français

Mark and share
Search through all dictionaries
Translate…
Search Internet

Share the article and excerpts