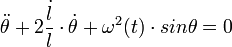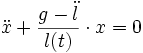Pendule de longueur variable

Pendule de longueur variable

Pendule simple de longueur variable

La charge soulevée par une grue est un pendule simple de longueur variable l(t). En considérant simplement les petites oscillations, pour raison de simplicité, on peut montrer que descendre la masse réduit l'oscillation (a contrario, lever la masse amplifie l'oscillation).

Une calcul plus délicat s'impose pour effectuer le bilan d'énergie.

Sommaire

Equation du mouvement

Le fil supportant la masse m est de masse négligeable , sans raideur et inextensible. Sa longueur est l(t) = OM ,O étant fixe.

Le théorème du moment cinétique appliqué en O donne :

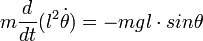m {d \over dt}{(l^2\dot{\theta})} = - mgl \cdot sin \theta, soit
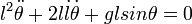l^2 \ddot{\theta} + 2 l \dot{l} \dot{\theta} + gl sin \theta = 0 , soit
\ddot{\theta} + 2 \frac{\dot{l}}{l} \cdot{\dot{\theta}} + \omega^2(t)\cdot sin \theta = 0

Interprétation

Le deuxième terme de l'équation se comporte comme une résistance positive si l(t) augmente, et a contrario, comme une résistance négative si l(t) diminue.

Ce raisonnement, souvent lu dans de la littérature de bonne qualité, est faux, et l'erreur est à chercher dans le terme "pulsation variable" , qui introduit en quelque sorte une "résonance paramétrique (On sait par ailleurs qu'en changeant de fonction inconnue on peut modifier à son gré le terme « dit de résistance »).

Maintenir cette erreur conduirait aisément à une décroissance de l'amplitude en 1/l(t), ce qui est faux pour l(t) lentement variable : on trouve l3(t)θ4(t) = cste, ce qui n'a rien d'intuitif.

Il convient aussi de faire le bilan énergétique du système : comment de l'énergie a-t-elle été transférée au degré d'oscillation , via l'allongement de l(t)? Car si le raisonnement par le théorème du moment cinétique a l'avantage d'être exact, il masque le fait que l'opérateur tire sur la ficelle et fournit du travail.

On peut très classiquement faire disparaître le terme de résistance par changement de jauge : on choisit l'arc AM = 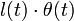l(t) \cdot \theta(t) := x , comme nouvelle inconnue et l'on trouve une équation particulièrement simple :

\ddot{x} + \frac{g-\ddot{l}}{l(t)} \cdot{x} = 0

L'accélération g a été "renormalisée" en g(t)= g - l" , ce qui n'a rien d'intuitif, on le voit par cette démonstration, sophistiquée s'il en est.

Dès lors,

  • Si l(t) varie lentement la méthode WKB donne la solution  : voir le pendule adiabatique.L'amplitude de x(t) varie comme sqrt(sqrt(l(t))), ce qui est bien le résultat indiqué plus haut.
  • Si l(t) = lo + v.t , alors l'équation devient une équation de Bessel : voir le pendule de Bessel. On peut aussi attaquer le problème avec les fonctions d'Airy.
  • Si l" = g , on reste intrigué, avec une attitude circonspecte.Bref, il faut refaire le calcul, dans ce cas-limite ; la ficelle en effet doit rester tendue!

Bilan d'énergie

Le bilan d'énergie du pendule de longueur variable est un exercice-de-style redoutable. Il faut retrouver la conservation de l'énergie, mais il convient d'être précautionneux.

On appelle U, V et W les quantités énergétiques :

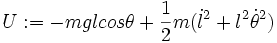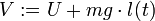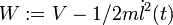
U : = -mgl cos\theta + \frac{1}{2}m(\dot{l}^2 + l^2 \dot{\theta}^2) et V := U + mg\cdot l(t) et W : = V -1/2 m {\dot{l}}^2(t)

Quand on veut dire que de l'énergie a été transférée, il faudra bien distinguer entre U, V et W . Soit aussi x = l .theta : Attention, l'énergie cinétique N'EST PAS 1/2 m l² (theta')² (car il faut rajouter 1/2 m (l')^2 ): il faut donc être assez pointilleux.

Soit T la tension du fil que tient l'expérimentateur. Puisque la perle-de-céramique en O a été considérée sans frottement , le travail fourni au système est -T dl/dt=dU/dt (équation E ).

On notera theta(t) l'élongation angulaire: les deux équations du mouvement sont :

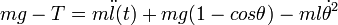
  • (1) :mg -T = m \ddot{l}(t) +mg(1-cos \theta)- ml{\dot{\theta}}^2
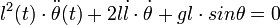
  • (2) :l^2(t) \cdot \ddot{\theta}(t) + 2 l\dot{l}\cdot \dot{\theta} + gl\cdot sin\theta = 0

et on peut vérifier la pertinence de chaque terme et vérifier que l'équation (2) est simplement l'équation trouvée au tout début :

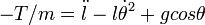
  • (1-bis): -T/m = \ddot{l} - l{\dot{\theta}}^2+gcos \theta
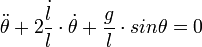
  • (2-bis): \ddot{\theta} + 2 {\dot{l}\over l}\cdot \dot{\theta} + {g \over l}\cdot sin\theta = 0


Le principe de Galilée fait que la masse m se simplifie et disparaît des calculs ; autant la prendre égale à l'unité ; il reste à reporter la valeur de T tirée de (1-bis)dans (E):

{dU \over dt} = {d \over dt}[-gl cos\theta + \frac{1}{2}(\dot{l}^2 + l^2 \dot{\theta}^2)] = [\ddot{l} +gcos \theta- l{\dot{\theta}}^2]\dot{l}--est-ce-vrai?


OUI! après pas mal de calculs et de simplifications venant de (2-bis)! Il y a bien conservation de l'énergie (heureusement!), mais on voit que cette vérification est loin d'être intuitive.Elle constitue un excellent exercice de "calcul" en force-brute.

  • Note : il est possible de mettre ce dernier calcul sous une forme un peu plus agréable du point de vue physique en introduisant V et W.

Si l'on considère le mouvement lent, on retrouve les résultats du pendule adiabatique :W~(lA)²/l varie comme 1/sqrt(l)

Autre expérience

Au lieu de laisser filer le fil au travers de la perle située en O, on peut au contraire élever la perle-de-céramique en A , l(t) =OA(t) avec une vitesse dl/dt. L'analyse est la même à condition de se placer dans le référentiel accéléré R ( origine A) où la pesanteur apparente est simplement g - l". L'équation en x(t) se simplifie encore ; en fait il faudrait montrer l'identité des deux expériences ; mais là aussi le bilan d'énergie requiert beaucoup d'attention.

Voir aussi

  • Portail de la physique Portail de la physique
Ce document provient de « Pendule simple de longueur variable ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Pendule de longueur variable de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Pendule simple de longueur variable — Le pendule simple de longueur variable modélise une charge soulevée par une grue. Quand la longueur se raccourcit, l amplitude des oscillations augmente et la puissance du moteur de la grue ne se réduit plus à lutter contre la pesanteur. Sommaire …   Wikipédia en Français

  • Pendule de bessel — Le pendule simple de longueur variable Quand la longueur d un pendule simple varie de manière affine: l(t)= lo + vt, on dit qu il s agit d un pendule de Bessel, car la solution (pour de petites oscillations) s exprime à l aide des fonctions de… …   Wikipédia en Français

  • Pendule de Bessel — Le pendule simple de longueur variable Quand la longueur d un pendule simple varie de manière affine: l(t)= lo + vt, on dit qu il s agit d un pendule de Bessel, car la solution (pour de petites oscillations) s exprime à l aide des fonctions de… …   Wikipédia en Français

  • Pendule adiabatique — On appelle équation du pendule adiabatique l équation différentielle : . lorsque la pulsation ω varie lentement; on dit alors qu il y a adiabatisme mécanique. L analyse WKB conduit à la remarquable conclusion qu il existe un invariant… …   Wikipédia en Français

  • Pendule simple à résonance paramétrique — En mécanique, un pendule paramétrique est un oscillateur où la force de rappel varie périodiquement. Cette situation dite de Hill (théorie de la Lune) de Mathieu (balancelle) ou de Bloch (électron dans un métal) est fréquemment utilisée en… …   Wikipédia en Français

  • Pendule pesant compose — Pendule pesant composé Un pendule pesant composé est un dispositif utilisé en physique. Il est constitué d un corps lié à un centre ou un axe de rotation et oscillant sous l effet de son propre poids. Il est dit composé par opposition au pendule… …   Wikipédia en Français

  • Pendule simple — Schéma montrant un pendule simple. En physique, le pendule simple est une masse ponctuelle fixée à l extrémité d un fil sans masse, inextensible et sans raideur[1] et oscillant sous l effet de la pesanteur. Il s agit du modèle de pen …   Wikipédia en Français

  • Pendule pesant composé — Un pendule pesant composé est un dispositif utilisé en physique. Il est constitué d un corps lié à un centre ou un axe de rotation et oscillant sous l effet de son propre poids. Il est dit composé par opposition au pendule simple car,… …   Wikipédia en Français

  • Balancelle — En mécanique du point, la balancelle est un pendule simple de longueur variable, où l enfant accroît l amplitude de ses oscillations par l action d un travail intérieur : en ce sens, le mécanisme est légèrement différent de celui d un… …   Wikipédia en Français

  • Det — Déterminant (mathématiques) Pour les articles homonymes, voir Déterminant. En mathématiques, initialement introduit en algèbre pour déterminer le nombre de solutions d un système d équations linéaires, le déterminant se révèle un outil très… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”