Partition entière

Une partition d'un entier strictement positif n est une façon d'écrire n comme une somme d'entiers strictement positifs. Deux sommes qui diffèrent seulement de l'ordre de leurs opérandes sont considérées comme étant la même partition. Un opérande dans une partition est aussi appelé une partie.

Une partition est aussi parfois appelé partage d'un entier.

Sommaire 1 Définitions 1.1 Partition d'un entier 1.2 k-partition d'un entier 2 Exemples 3 Graphe de Ferrer 4 Nombre de partages 5 Voir aussi 5.1 Liens internes 5.2 Référence bibliographiques

Définitions

Partition d'un entier

Soit 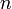un entier strictement positif, une partition de 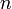est une suite d’entiers 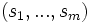vérifiant

•  ;
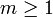• tous les entiers 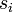sont non nuls ;
• .

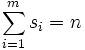k-partition d'un entier

Une k-partition de l'entier n est une partition de n possédant k éléments.

Exemples

Les partitions de 4 sont listés ci-dessous :

• 4 = 3 + 1 = 2 + 2 = 2 + 1 + 1 = 1 + 1 + 1 + 1

Voici les partitions de 8 :

• 8
• 7 + 1
• 6 + 2
• 6 + 1 + 1
• 5 + 3
• 5 + 2 + 1
• 5 + 1 + 1 + 1
• 4 + 4
• 4 + 3 + 1
• 4 + 2 + 2
• 4 + 2 + 1 + 1
• 4 + 1 + 1 + 1 + 1
• 3 + 3 + 2
• 3 + 3 + 1 + 1
• 3 + 2 + 2 + 1
• 3 + 2 + 1 + 1 + 1
• 3 + 1 + 1 + 1 + 1 + 1
• 2 + 2 + 2 + 2
• 2 + 2 + 2 + 1 + 1
• 2 + 2 + 1 + 1 + 1 + 1
• 2 + 1 + 1 + 1 + 1 + 1 + 1
• 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1

Parmi les 22 partitions du nombre 8, 6 d'entre eux contiennent seulement des parties impaires :

• 7 + 1
• 5 + 3
• 5 + 1 + 1 + 1
• 3 + 3 + 1 + 1
• 3 + 1 + 1 + 1 + 1 + 1
• 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1

Curieusement, si nous comptons les partitions de 8 en « parties distinctes », nous obtenons aussi le nombre 6 :

• 8
• 7 + 1
• 6 + 2
• 5 + 3
• 5 + 2 + 1
• 4 + 3 + 1

Est-ce seulement une coïncidence, ou est-il vrai que pour tout entier strictement positif, le nombre de partitions en parties impaires est toujours égal au nombre de partitions ayant des parties distinctes ? Ce type de résultats et d'autres peuvent être obtenus à l'aide d'un outil visuel, le graphe de Ferrer.

Graphe de Ferrer

La partition 6 + 4 + 3 + 1 de l'entier strictement positif 14 peut être représenté par le graphe suivant :

o o o o
o o o
o o o
o o
o
o

6+4+3+1 

Les 14 cercles sont alignés sur 4 colonnes, chacune ayant la grandeur d'une partie de la partition. Les graphes pour les 5 partitions du nombre 4 sont listés ci-dessous :

o   o o   o o   o o o   o o o o
o   o     o o   o
o   o
o

4   3+1   2+2   2+1+1   1+1+1+1

Maintenant, si nous effectuons une symétrie du graphe de la partitions de 6 + 4 + 3 + 1, par rapport à la diagonale principale :

o o o o         o o o o o o
o o o           o o o o
o o o     -->   o o o
o o             o
o
o

6+4+3+1         4+3+3+2+1+1

En transformant les lignes en colonnes, nous obtenons la partition 4 + 3 + 3 + 2 + 1 + 1 du nombre 14. De telles partitions sont dits conjuguées l'une de l'autre. Dans le cas du nombre 4, les partitions 4 et 1 + 1 + 1 + 1 sont conjugués, ainsi que les partitions 3 + 1 et 2 + 1 + 1. La partition 2 + 2 présente un certain intérêt, puisqu'elle est sa propre conjuguée. Un tel partage est dit auto-conjugué.

Proposition Le nombre de partitions auto-conjugués est le même que le nombre de partages en parties impaires distinctes.

Schéma de la démonstration: Le fait essentiel est que toutes les parties impaires peuvent être « pliées » en leur milieu pour former un graphe auto-conjugué :

o
o
o   -->   o o o
o         o
o         o

Nous pouvons alors construire une bijection entre l'ensemble des partitions en parties impaires distinctes et l'ensemble des partitions auto-conjugués, comme l'illustre très bien l'exemple suivant:

    o * x          o o o o o   
    o * x          o * * * *   
    o * x   <-->   o * x x     
    o *            o * x       
    o *            o *         
    o *                        
    o *                        
    o                          
    o                          
 
    9+7+3          5+5+4+3+2   

impair distinct auto-conjugué

Des techniques similaires peuvent être employées pour établir, par exemple, les égalités suivantes :

• Le nombre de partitions de n en au plus k parties est égal au nombre de partitions de n en parties inférieures à k.
• Le nombre de partitions de n en moins de k parties est égal au nombre de partitions de n+k en exactement k parties.

Nombre de partages

Le nombre de partages d'un entier strictement positif n est donné par la fonction partage p. Le nombre de partages de n en exactement k parties est noté p_k(n).

Les techniques des graphes de Ferrer nous permettent aussi de prouver des résultats comme le suivant :

• Il y a p(n) - p(n-1) partages de n dans lesquels chaque partie est supérieure à 2.
• p(1) + p(2) + ... + p(n) < p(2n)

Voir aussi

Liens internes

• Fonction partage d'un entier
• Graphe partitionable

Référence bibliographiques

Une introduction élémentaire à la notion de partition d'un entier, incluant les graphes de Ferrer, peut être trouvée dans l'ouvrage suivant :

Miklós Bóna, A Walk Through Combinatorics: An Introduction to Enumeration and Graph Theory, World Scientific Publishing, 2002. ISBN 981-02-4900-4.

• Portail des mathématiques