Paramètre d'Oort

Constantes d'Oort

Pour les articles homonymes, voir Oort.

Les constantes d'Oort ou paramètres d'Oort sont des coefficients qui mesurent les propriétés du champ de vitesse dans le disque galactique au voisinage solaire. Ils sont nommés en l'honneur de l'astronome hollandais Jan Oort qui les a introduits en 1927 en démontrant par là même la réalité de la rotation des étoiles autour du centre de la Voie lactée^[1].

Dans l'hypothèse où les trajectoires des étoiles dans les galaxies sont circulaires et que leur vitesse ne dépend que de leur distance au centre, il est possible observationnellement de déterminer la vitesse angulaire des étoiles dans le voisinage solaire ainsi que sa dépendance locale par rapport à la distance du Soleil au centre galactique par la seule observation de la vitesse radiale et du mouvement propre d'autres étoiles proches par rapport au Soleil.

Sommaire

1 Formule
2 Cas particuliers
3 Utilisation
4 Valeurs numériques
5 L'étude du voisinage solaire avec les constantes d'Oort
6 Voir aussi
7 Notes
8 Références

Formule

Les constantes d'Oort sont au nombre de deux, notées A et B suivant les notations introduites par Oort en 1927. Elles interviennent dans la valeur prédite de la vitesse radiale V_r (mesurable par spectroscopie) et la vitesse tangentielle 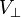$V_\perp$ (mesurable par mouvement propre) des étoiles situées à une distance r du Soleil selon les formules

V r = r A sin(2(l - l 0))

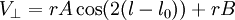$V_\perp = r A \cos (2 (l - l_0)) + r B$ ,

où l représente une longitude galactique dans un système de coordonnées galactiques dans lequel le centre galactique (a priori indéterminé) est situé à la longitude l₀.

Les constantes d'Oort A et B ont la dimension d'une vitesse divisée par une longueur et s'expriment traditionnellement en km⋅s^-1⋅kpc^-1. Elles sont reliés à la vitesse orbitale V au voisinage solaire et sa dérivée par rapport à la distance R au centre par :

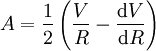$A=\frac{1}{2}\left(\frac{V}{R}-\frac{{\rm d}V}{{\rm d}R}\right)$ ,
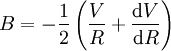$B=-\frac{1}{2}\left(\frac{V}{R}+\frac{{\rm d}V}{{\rm d}R}\right)$ ,

ces valeurs étant évaluées au voisinage solaire.

Démonstration

On se place dans la plan galactique dans lequel le centre galactique est à la longitude l₀. Les coordonnées du Soleil dans ce plan sont donc :

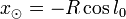$x_\odot = - R \cos l_0$ ,

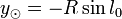$y_\odot = - R \sin l_0$ .

On suppose le Soleil animé d'un mouvement circulaire de vitesse V, et on définit l'orientation des coordonnées galactiques par le fait que le Soleil se dirige vers la direction l = 90°dont les coordonnées sont donc

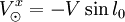$V^x_\odot = - V \sin l_0$ ,

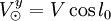$V^y_\odot = V \cos l_0$ .

Soit une étoile, dont le mouvement est également supposé circulaire, situé à une distance r du Soleil et à la longitude l. On suppose la distance de l'étoile r petite devant la distance au centre galactique R. Les coordonnées de l'étoile dans le plan galactique sont

x * = - R cos l 0 + r cos l

y * = - R sin l 0 + r sin l

La distance de cette étoile au centre galactique est approximativement

D * = R - r cos(l - l 0)

La vitesse de cette étoile par rapport au centre galactique est, en valeur absolue,

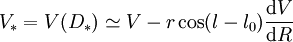$V_* = V(D_*) \simeq V - r \cos (l - l_0) \frac{{\rm d} V}{{\rm d} R}$ .

L'angle fait la direction étoile-centre galactique diffère de la direction Soleil-centre galactique par la valeur

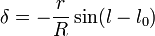$\delta = - \frac{r}{R} \sin (l - l_0)$ ,

de sorte que les coordonnées de la vitesse de l'étoile s'écrivent

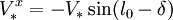$V^x_* = - V_* \sin (l_0 - \delta)$ ,

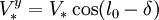$V^y_* = V_* \cos (l_0 - \delta)$ .

La vitesse relative de l'étoile par rapport au soleil est donc

δ V x = - V * sin(l 0 - δ) + V sin l 0

δ V y = V * cos(l 0 - δ) - V cos l 0

En développant ces expressions et en ne gardant que les termes de l'ordre le plus bas, il vient

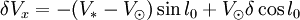$\delta V_x = - (V_* - V_\odot) \sin l_0 + V_\odot \delta \cos l_0$ ,

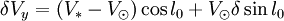$\delta V_y = (V_* - V_\odot) \cos l_0 + V_\odot \delta \sin l_0$ .

La composante de cette vitesse relativement à la direction de l'étoile donne la vitesse radiale de celle-ci. Elle vaut

V r = δ V x cos l + δ V y sin l

Elle vaut

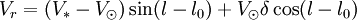$V_r = (V_* - V_\odot) \sin (l - l_0) + V_\odot \delta \cos (l - l_0)$ .

En remplaçant les termes 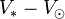$V_* - V_\odot$ et $δ$ par leur valeur trouvée plus haut, il vient

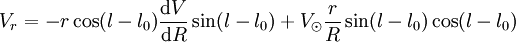$V_r = - r \cos (l - l_0) \frac{{\rm d} V}{{\rm d} R} \sin (l - l_0) + V_\odot \frac{r}{R} \sin (l - l_0) \cos (l - l_0)$ ,

que l'on peut combiner en

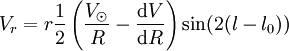$V_r = r \frac{1}{2} \left(\frac{V_\odot}{R} - \frac{{\rm d} V}{{\rm d} R} \right) \sin (2(l - l_0))$ ,

ou bien

V r = r A sin(2(l - l 0))

en utilisant la définition de A ci-dessus.

La composante perpendiculaire de vitesse se calcule selon

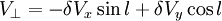$V_\perp = - \delta V_x \sin l + \delta V_y \cos l$ ,

ce qui donne

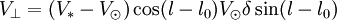$V_\perp = (V_* - V_\odot) \cos (l - l_0) V_\odot \delta \sin (l - l_0)$ .

En remplaçant à nouveau les deux quantités par leurs valeurs précédemment trouvées, il vient

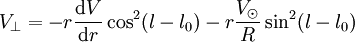$V_\perp = - r \frac{{\rm d} V}{{\rm d} r} \cos^2(l - l_0) - r \frac{V_\odot}{R} \sin^2 (l - l_0)$ ,

qui se combine en

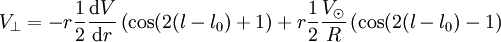$V_\perp = - r \frac{1}{2} \frac{{\rm d} V}{{\rm d} r} \left(\cos(2(l - l_0) + 1\right) + r \frac{1}{2} \frac{V_\odot}{R} \left( \cos(2(l - l_0) - 1\right)$ ,

soit

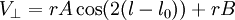$V_\perp = r A \cos(2 (l - l_0)) + r B$ .

Cas particuliers

Rotation solide

Dans le cas où la galaxie est animée d'une rotation solide, c'est-à-dire d'une vitesse angulaire V/R indépendante de la distance, alors la quantité A est nulle et la quantité B est égale à l'opposé de la vitesse angulaire :

A s = 0

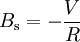$B_{\rm s} = - \frac{V}{R}$ .

Rotation képlérienne

Si la masse de la galaxie est concentrée au centre, alors la vitesse varie conformément à la troisième loi de Kepler, c'est-à-dire selon

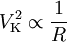$V_{\rm K}^2 \propto \frac{1}{R}$ .

À ce moment là, A et B sont reliés par

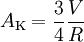$A_{\rm K} = \frac{3}{4} \frac{V}{R}$ ,

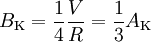$B_{\rm K} = \frac{1}{4} \frac{V}{R} = \frac{1}{3} A_{\rm K}$ .

Courbe de rotation plate

Si le profil de densité est tel que la vitesse soit indépendante de la distance, comme cela est observé dans la périphérie de nombreuses galaxies spirales, alors le terme en dérivée et nulle et A et B sont opposés :

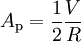$A_{\rm p} = \frac{1}{2} \frac{V}{R}$ ,

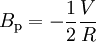$B_{\rm p} = - \frac{1}{2} \frac{V}{R}$ .

Utilisation

Dans l'hypothèse où la quantité A n'est pas nulle, il apparaît une modulation à la fois dans la vitesse radiale et dans le mouvement propre qui donne la direction du centre galactique, vers laquelle le vitesse radiale est nulle et le mouvement propre est maximal. La cohérence du modèle est alors observée par le fait que la modulation de la vitesse tangentielle 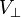$V_\perp$ est en quadrature avec la vitesse radiale (l'une est maximale en valeur absolue quand l'autre est nulle).

Dans tous les cas, la mesure de A ou B à une valeur non nulle permet de prouver la rotation galactique. Si une modulation est observée dans la vitesse radiale et/ou tangentielle, alors on met en évidence la rotation différentielle de la galaxie, ce que Oort fut le premier à réaliser en 1927, bien que d'autres avant lui en aient eu l'intention (notamment Bertil Lindblad qu'Oort cite abondamment dans son article de 1927).

Valeurs numériques

La quantité A est la plus facile à mesurer, car elle se fait à l'aide des vitesses radiales, dont la mesure est aisée quelle que soit la distance. Celle de B est considérablement plus ardue, car elle nécessite la connaissance de mouvements propres à une haute précision. De plus, le mouvement des étoiles n'est pas en général circulaire. Pour mettre en évidence le résultat, il est donc nécessaire de moyenner le mouvement des étoiles dans une région donnée. À ceci s'ajoute que le Soleil lui-même a une trajectoire s'écartant significativement d'une orbite circulaire. Ainsi, la vitesse radiale et la vitesse tangentielle sont-elles affectées par la composante supplémentaire venant du Soleil, composante qui doit être enlevée avant d'estimer A et B. Observationnellement, cette composante supplémentaire affecte la direction vers laquelle se déplace le Soleil dans notre Galaxie, direction appelée apex solaire dont la connaissance précise est cruciale pour bien évaluer les mouvements des galaxies voisines de la nôtre au sein de la structure appelée Groupe local.

Les valeurs communément admises aujourd'hui sont :

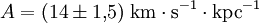$A = (14 \pm 1,\!5)\;{\rm km} \cdot {\rm s}^{-1} \cdot {\rm kpc}^{-1}$ ,

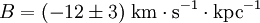$B = (-12 \pm 3)\;{\rm km} \cdot {\rm s}^{-1} \cdot {\rm kpc}^{-1}$ .

L'incertitude plus grande sur B résulte de la plus grande difficulté à le mesurer comme évoqué ci-dessus.

Numériquement, A et B sont opposés dans la limite des barres d'erreur, ce qui s'interprète comme une indication que le Soleil est situé dans la partie de courbe de rotation plate de notre Galaxie, résultat cohérent avec la valeur de la distance du Soleil au centre galactique comparée à l'extension spatiale totale de notre Galaxie.

L'étude du voisinage solaire avec les constantes d'Oort

On observe que les constantes d'Oort prennent des valeurs différentes selon le type de population stellaire étudiée. Cela résulte du fait que le voisinage solaire possède divers régions de formation d'étoiles d'où certaines populations jeunes sont préférentiellement issues. La ceinture de Gould, identifiée de longue date (par Benjamin Gould en 1879), est ainsi également mise en évidence par le biais qu'elle induit dans la détermination des constantes d'Oort.

Voir aussi

Notes

↑ (en) Jan Oort, Observational evidence confirming Lindblad's hypothesis of a rotation of the galactic system, Bulletin of the Astronomical Institutes of the Netherlands, 3, 275-282 (1927) Voir en ligne.

Références

Les constantes d'Oort sont évoqués dans tout document relatif à la dynamique de notre Galaxie. Voir par exemple

(en) Cours d'astronomie de Ned Wright, de l'Université de Californie à Los Angeles (pdf, 131 pages), p. 9 à 12.

Portail de l’astronomie

Ce document provient de « Constantes d%27Oort ».

Catégories : Voie lactée | Astrométrie

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Paramètre d'Oort de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

(90377) Sedna — Pour les articles homonymes, voir Sedna. (90377) Sedna Caractéristiques orbitales Époque 22 octobre 2004 (JJ 2453300,5) Demi grand axe 75,659770×109 km (505,754 ua … Wikipédia en Français
Equation — Équation (mathématiques) Cet article concerne les équations mathématiques dans leur généralité. Pour une introduction au concept, voir Équation (mathématiques élémentaires). … Wikipédia en Français
Équation — Cet article concerne les équations mathématiques dans leur généralité. Pour une introduction au concept, voir Équation (mathématiques élémentaires). … Wikipédia en Français
Équation (mathématiques) — Cet article concerne les équations mathématiques dans leur généralité. Pour une introduction au concept, voir Équation (mathématiques élémentaires). … Wikipédia en Français
Équation symétrique — Équation (mathématiques) Cet article concerne les équations mathématiques dans leur généralité. Pour une introduction au concept, voir Équation (mathématiques élémentaires). … Wikipédia en Français
Équation vectorielle — Équation (mathématiques) Cet article concerne les équations mathématiques dans leur généralité. Pour une introduction au concept, voir Équation (mathématiques élémentaires). … Wikipédia en Français
Équations — Équation (mathématiques) Cet article concerne les équations mathématiques dans leur généralité. Pour une introduction au concept, voir Équation (mathématiques élémentaires). … Wikipédia en Français
Petit corps du Système solaire — En astronomie, un petit corps du système solaire est un objet céleste du système solaire orbitant autour du Soleil et qui n est ni une planète, ni une planète naine[1]. Le terme fut adopté en 2006 par l Union astronomique internationale afin de… … Wikipédia en Français
Petit corps du systeme solaire — Petit corps du système solaire En astronomie, un petit corps du système solaire est un objet céleste du système solaire orbitant autour du Soleil et qui n est ni une planète, ni une planète naine[1]. Le terme fut adopté en 2006 par l Union… … Wikipédia en Français
Petit corps du système solaire — En astronomie, un petit corps du système solaire est un objet céleste du système solaire orbitant autour du Soleil et qui n est ni une planète, ni une planète naine[1]. Le terme fut adopté en 2006 par l Union astronomique internationale afin de… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Paramètre d'Oort

Constantes d'Oort

Sommaire

Formule